Анализ временных и частотных характеристик линейных цепей. Вид искомой передаточной функции

Федеральное агентство по образованию Рязанский Государственный Радиотехнический Университет

Кафедра ТОЭ

Курсовая работа по теме «Анализ временных и частотных характеристик линейных цепей»

Вариант №3

Выполнил:  ст.гр.№718

Проверил: 

Рязань, 2009.

Исходные данные

k=2; n=3

Вид искомой передаточной функции: Y₂₁

Схема активного четырехполюсника:  #1

Величина сопротивления ОС (R0 и R0' ): вариант В Используемые параметры транзистора: параметры Н

Номер транзистора: #1

Схема пассивного четырехполюсника: 3

Вариант исходных данных для пассивного четырехполюсника: В.

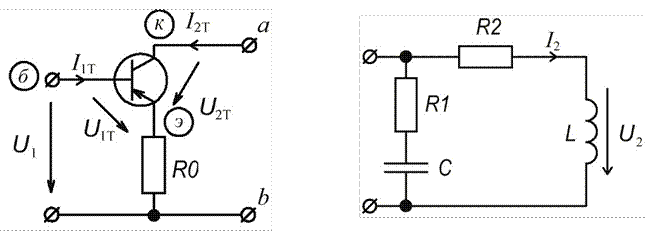
Рис.1                                                  Рис.2

Схема активного четырехполюсника – рис. 1, схема пассивного четырехполюсника – рис. 2 .

Н-параметры транзистора: Н₁₁ = 200 Ом, Н₁₂ = 2·10^-4 , Н ₂₁ = 30 ,  Н ₂₂=0.1 мСм

Величина сопротивления ОС: R0=100 Ом Параметры пассивного четырехполюсника:

R1 = 8 Ом, R2 = 5 Ом, L = 20 мкГн, С = 1.2 нФ.

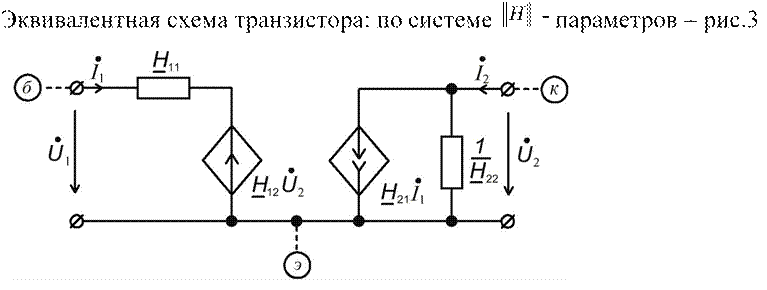
Рис.3

1. Получение передаточной функции   p        Iвых(p)        I5(p)

Искомая ПФ:                           Y21( )                                                (1)

                                             U_вх(p)      E(p)

Определение ПФ по полной схеме

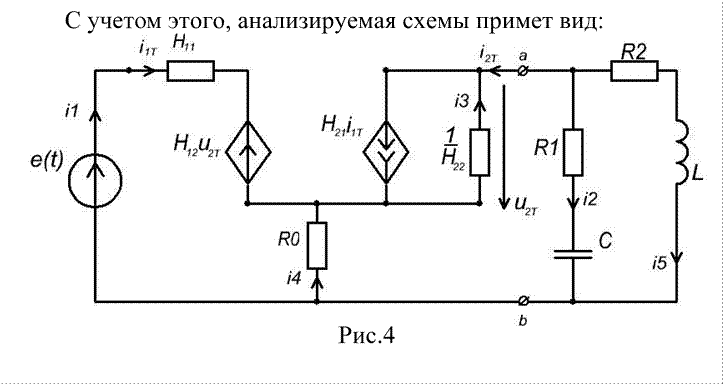
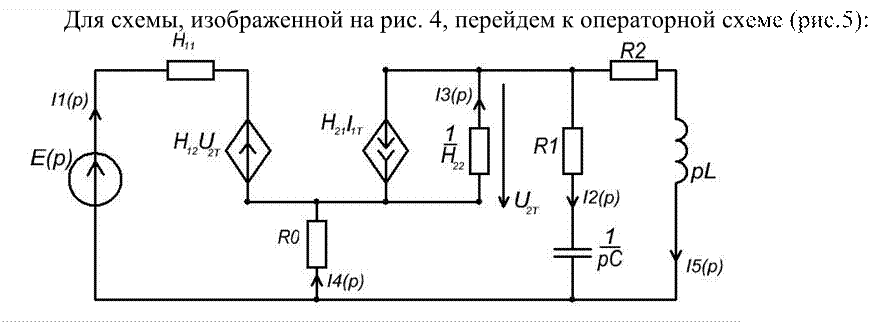
Рис.5

Для определения ПФ схемы, приведенной на рис. 5, запишем систему уравнений для определения токов в ветвях по законам Кирхгофа.  I₂(p) I₅(p) I₄(p) I₁(p)  0

^    I₁(p) I₄(p) I₃(p) H₂₁I_1T (p)  0

 I₁(p)H₁₁  I₄(p)R₀  E(p) H₁₂U_2T (p⁾                          (2)

_

^                                          I4(Ip₅)(                                                               pR)(0R₂I3(pLp))H122I                      ₂(pI2)_(Rp₁)R1pC1_pC1                                   0. 0                                                                                  

_{                                          }

При решении системы (2) учтем следующее:

1  E(p)

U_2Т(p)      I₃(p), I_1Т(p)   

H22                                                          H11

Рассмотрим решение системы (2) в пакете Mathcad 14. Find (I2, I3, I4, I5, I6, I7, U2) float, 5 →

1.0 (1.4995e20 p  1.562e28)      

Y21(p)  

2

2.7074e22 p  4.127e16 p  1.7195e30

Проводим необходимые математические преобразования для приведения ПФ к каноническому виду (Н₂(p) – промежуточный результат):

 1.4995         ²⁰                      3         1.562      ²⁸                      11        1.7195      ³⁰                      13      2.7074      ²² 5

 3.633 10 3.785 10 4.166 10 6.56 10

4.127 10                                     4.127 10                                    4.127 10                                4.127 10

3                        11                                     11

Y211(p)  3.633 10 p  3.785 10 3.785  1.042 108  p² _ 6.56 10⁵ _ p  4.166 10¹³ 3.633 10

Таким образом, выражение для ПФ для анализируемой схемы: 

₈

                        ^{H(p)  3.633 103}          ₂ ^p1.042                 ₅ ^10          ₁₃        (3)

p 6.5610 p4.16610

Представим полученную ПФ (3) в следующем виде:

  H(p) 3633 p2  6.56p101.5042 p 104.⁸1661013  FF₁2((pp)) ,M _{ }3633

Найдем нули и полюса ПФ. Корни уравнения F₁(p) = 0 – нули ПФ, а корни уравнения F₂(p) = 0 – полюса ПФ. F1(p)  p  1.042 108 F2(p)  p²  6.56 10⁵  p  4.166 10¹³  

F1(p)solvefloat 5p 1.042e8 F2(p)solvefloat5p ^ 328000.0328000.0 6.4461e66.4461e6ii^                                              

_{                        }

Полюсы p_x1,2  (0.328 j6.4461)10^{6 1}_c   j_св .

Число полюсов ПФ соответствует числу накопителей в схеме.  Сравним частоты свободных и резонансных колебаний:

_св  6.446110⁶ 1        _р           1       6.45510^{6 1}     _р _св с   LC       с

2. Получение выражений для АЧХ и ФЧХ

Для получения выражений АЧХ и ФЧХ необходимо вместо p в выражение (3) для ПФ Н(р) подставить jω и полученное выражение преобразовать к показательной форме:

H(j)  H(p)

 1.04210⁸  j

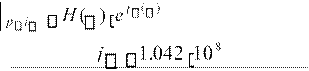 H( j^) ^{ }3633( j)²  6.5610⁵  j 4.16610^{13  }3633(4.16610¹³ _²)  j6.5610^{5 }

o                                                                          jarctg  8 

3633e j180       (1.042108 )2 ()2 e      1.04210 

                                                                    6.56105 

    (4.1661013 2 )2 (6.56105 )2 e jarctg 4.1661032 

3633  (1.04210⁸)²  ()²

H() (Ом) (4.16610¹³ _²)²  (6.5610⁵)²

() 180o  arctg 1.042 8 arctg 4.1666.105613105 2

10

При вычислениях значения каждого из арктангенсов, входящих в выражение для ФЧХ, берутся в соответствии со знаками действительной и мнимой частей. Построим графики АЧХ И ФЧХ в пакете Mathcad 2000 (рис. 6 и 7).

3                      p  1.042 108

H(p)  3.633 10 

p²  6.56 10⁵  p  4.166 10¹³

i    104200000.000

Hj  H(p) substitute p  i    3633.000

²  656000.00 i    41660000000000.000

 

H1  Hj   argHj

  1105107

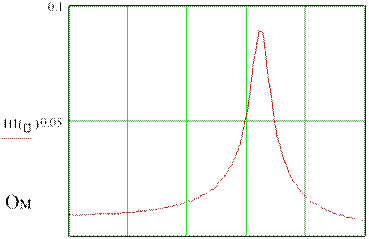Н (=0) = 0.00908

Н () = 0.01816

Рис. 6

0 0            2 10⁶             4 10⁶             6 10⁶             8 10⁶             1 10⁷



(=0) = 180

() = 0

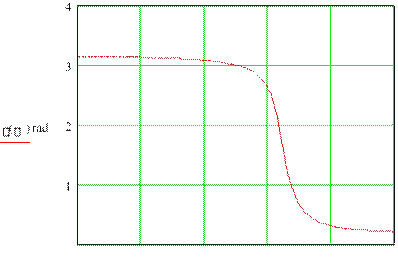         0             6                6                     6                    6                   7        Рис. 7

0             2 10           4 10       _ 6 10           8 10           1 10

3. Расчет переходной h(t) и импульсной g(t) характеристик

Получение выражений для переходной h(t) и импульсной g(t) характеристик основано на переходе от изображения к оригиналу на основе теоремы разложения:

h(t)  L1H(pp) и g(t) L1H(p).



Расчет переходной характеристики h(t)

 H(p)  ³⁶³³   p²  6.56p 101.042⁵  p10 4⁸.16610¹³) ^ pF₁F(₂p()p) ^ FF₁₃((pp))  p           ^{ }     p(

Так как корни знаменателя F₃(p) p₁ = 0 и  p_2,3  (0.328 j6.4461)10^{6 1}_с   j_св , то вид искомой h(t):

h(t)  A1e^p1t  2A2 e^t cos(св t ),

где A1  FF1((pp11)) ; A2  FF31((pp22))  А2 е j, p2  (0.328 j6.4461)106.

3

F₃^(p)  3p² 1.31210⁶ p  4.16610¹³.

A1  FF_31((00))  36334.1661._042101310⁸  0.00908,

A2  F₁((0.328F_3(j_p62.4461₎ )10⁶ )  А₂ е _j.                                                      (4)

F1(p)  3633 p  1.042 10⁸

F3(p)  p  p²  6.56 10⁵  p  4.166 10¹³ F3pr(p)  3p²  1.312 10⁶  p  4.166 10¹³ p2  (0.328 j  6.4461)  10⁶

F1(p2) A2komp F3pr(p2)

A2komp  4.543 10^3  5.061i 10^5

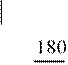A2   A2komp A2  4.544 10^3  arg(A2komp)    0.638



6 h(t)  0.00908 2  4.544 10^3e^{0.32810 t}  cos6.441 10⁶t  0.638

Расчет импульсной характеристики g(t)

H(p) 3633 2 36336.5610p 5 3p.785 4.16610¹¹1013  FF₄2((pp))  p   p 

F₂(p) = 0  p_1,2  (0.328 j6.4461)10^{6 1}_с   j_св вид искомой g(t):

g(t) (t)2A₁ e^t cos(_св t )^,

A1  F4((pp11))  А1 е j, p1  (0.328 j6.4461)106. F2

A1  F₄(0.328_(j_p61.4461₎ )10⁶  А1 е j.                                                         (5)

_F2

Проведем решение выражения (5) в пакете Mathcad 2000.

F4(p)  3633 p  3.785 10¹¹

F2(p)  p²  6.56 10⁵  p  4.166 10¹³

F2pr(p)  2  p  6.56 10⁵ p1  (0.328 j  6.4461)  10⁶

F4(p1) A1komp F2pr(p1)

A1komp  1.816 10³  2.927i 10⁴

A1   A1komp                            A1  2.932 10⁴

180

 arg(A1komp)                    93.552

                                                

g(t)  2 2.932 104  e0.328106t  cos6.4461 106  t  deg  93.552

Для проверки правильности полученных результатов сопоставим выражения