Определение, формы представления графов. Матрица смежности для орграфа. Цикл Эйлера и цикл Гамильтона, страница 7

В отличие от цикломатического числа определение хроматического числа осуществляется с помощью сравнительно сложных алгоритмов, поэтому дадим здесь лишь оценку хроматического числа через число вершин n cвязного графа G и через степени его вершин d_i(х):

1 £ К(G) £ n;

k(G) £ d_max (х) = max d(х_i)

х_i Î X.

Если K(G)=2, то граф G называется бихроматическим или двудольным, т.к. множество вершин Х в нем может разбить на два непересекающихся подмножества Х1 и Х2, в каждом из которых все вершины несмежны и окрашены в один цвет Пример двудольного графа приведен на рис. 7.1. Необходимое и достаточное условие бихроматичности графа состоит в том, чтобы все простые циклы в нем имели четную длину[1].
Например, для графа на рис. 7.1.длина цикла (x1, х6, х2, х5, х1) равна четырем, длина цикла (х2, х5, х4, х9, х8, х6, х2) равна шести.

Заметим, что дерево всегда является двудольным графом.

На пра:Ѐтике для связный графов оценить величину К(G)  можно, с помощью различных приближенных алгоритмов. Например, с помощью следующей процедуры[(](. Выбираем вершину с максимальной степенью (еслитаких несколько, то любую из них) и раскрашиваем ее в цвет 1. Затем, просматривая все неокрашенные вершины, в цвет 1 раскрашиваем всякую величину, не смежную с уже окрашенными в этот цвет вершинами.

Среди оставшихся неокрашенными вершин вновь выбираем вершину с максимальной степенью и окрашиваем ее в цвет 2, затем в тот же цвет окрашиваем всякую вершину, не смежную с уже окрашенными в цвет 2.

Аналогично действуем с цветами 3, 4 и т.д., пока не будут окрашены все вершины.

Число использованных цветов будет приближенным значением хроматического числа графа. В качестве примера найдем оценку К(G) для графа на рис. 7.2.

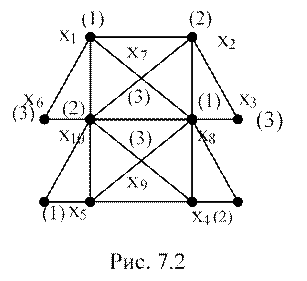В цвет 1 окрашиваем вершины: х₈, х₁, х₅;

В цвет 2 : х₁₀,  х₂,  х₄;

В цвет 3: х₇, х₉, х₃, х₆.

Таким образом, оценка хроматического числа для графа на рис. 7.2. равна 3.

Упражнения.

6.1.1.  Чему равно хроматическое число полного графа? Нуль графа?

6.1.2.  Привести примеры простых циклов для графа на рис. 7.1

6.1.3.  Привести пример плоского графа с восемью вершинами и найти оценку его хроматического числа.

6.2.  Число внутренней устойчивости (независимости)

Если в неориентированном графе G (Х, А) имеется некоторое подмножество S_i Ì X несмежных между собой вершин, т.е. (" х_i Î S_i) [Г(х_i) ∩ S_i = Æ],

То такое подмножество называется внутренне устойчивым или независимым множеством .[2,4]

Например, для графа на рис. 7.2. множества вершин s₁={x₂, x₄}, S₂{х₁, х₅, х₈}, S₃{х₇, х₉, х₃, х₆} - внутренне устойчивые или независимые множества.

Независимое множество называется непополнимым, или максимальным, если его нельзя дополнить ни одной вершиной х_i Î Х без потери свойств независимости. Так, множества S₁ и S₂ являются непополнимыми, а множество S₁ таковым не является, т.21к. при добавлении к нему вершины _х8 свойство независимости вершин сохраняется.

Если имеется семейство S всех независимых множеств, то подмножество с иаксимальной мощностью называется наибольшим независимым (внутренне устойчивым) множеством, а величину равную мощности этого множества, называют числом независимости или числом внутренней устойчивостиa(()(:a(()(=( ma½(S½(.

SiÎ( S

Очевидно, что наибольшее независимое множество является непополняемым. Иными словаи, числом внутренней устойчивости называют максимальное число несмежных вершин графа.

Для графа на рис. 7.2. наибольшее независимое множество есть S₃ = {х₇, х₉, х₃, х₆ }, и a(G) = 4.

6.3.  Кликовое число .