Определение, формы представления графов. Матрица смежности для орграфа. Цикл Эйлера и цикл Гамильтона

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ

Методические указания к практическим

занятиям по курсу «Основы САПР»

Составили:       доц.

асс. асс.

УДК 519.9

Основные понятия теории графов: Методические указания  к практическим  занятиям / Рязан. гос. радиотехн.

Содержит основные сведения о формах представления, частях и типах графов, разделы, посвященные операциям над графами, характеристическим числам графа, деревьям и плоским графам. Все разделы содержат поясняющие примеры и упражнения.

Предназначены для студентов дневного отделения специальности 22.03.

Ил. 22. Библиограф. : 5 назв.

Печатается  по решению методического совета Рязанской государственной радиотехнической академии.

Рецензент: кафедра САПР ВС Рязанской государственной радио-технической академии (зав. кафедрой САПР ВС, академик МАИ, профессор ).

1. Определение, формы представления графов.

Граф G  задается множеством точек или вершин х1, х2,…хn (которое обозначим через Х ), и множеством отрезков а1, а2,…аn (которое обозначим символом А), соединяющих между собой все или часть этих точек. Математически граф G полностью задается парой (Х, А): G = (Х, А).

Если отрезки из множества А ориентированы, что обычно показывается стрелками в геометрическом представлении графа, то они называются дугами, а граф называется ориентированным графом (орграфом) (рис.1.1.) Если отрезки не имеют ориентации, то они называются ребрами, а граф– неориентированным. (рис. 1.2.)

 

Часто употребляется другое, аналитическое описание орграфа [2]. Задается множество вершин Х и соответствие Г, которое показывает как связаны между собой эти вершины. Соответствие Г называют отображением множества Х в Х, а граф тогда обозначается парой G = (Х, Г). Соответствие Г(хi) – множество таких вершин хj ( Х, для которых в графе G существует дуга (хi, хj). Дуга, отображающая вершину в саму себя, называется петлей (дуга а4 на рис.1.1). Например, для вершин х1, х2, х6 графа рис. 1.1. имеем :

Г(х1) = {х5, х6},

Г(х2) = {х2, х4},

Г(х6) = (.

Соответствие Г-1(хi) называют обратным (инверсным) соответствием, понимая под ним множество вершин хк ( Х, для которых в G cуществует дуга (хк, хi). Для графа рис.1.1 Г-1(х1) = {х5}, Г-1(х2) = {х2,х3},Г-1(х6)={х1,х 5}.

В случае неориентированного графа или смешанного (содержащего и дуги и ребра) предполагается, что соответствие Г задает такой эквивалентный орграф, который получается из исходного заменой каждого ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Так, для вершин х1 и х2 графа на рис.1.2. имеем:

Г(х1) = Г-1 (х1) = {х 2, х 4, х 5};  Г(х2) = Г-1 (х2)  = {х 1, х 3, х 5}.

Отображение Г множества вершин Хк = {х1, х2,..., хк} есть объединение отображений этих вершин:

Г(Хк) = Г(х1) ( Г(х2) (…È Г(х_к).

Например, для графа рис. 1.1 Г({х ₁, х ₂, х ₆} ) = {х ₂, х _4, х ₅, х ₆}; Г({х ₃, х ₄, х ₅} ) = {х ₁, х _2, х _3,х ₄, х ₆ }.

Матричное представление графов осуществляется в виде матриц смежности и инциденций (инцидентности).

Две вершины х_i и x_j являются смежными, если есть дуга (ребро), соединяющая обе вершины. Дуга a называется инцидентной вершине х, если заходит в эту вершину или исходит из нее, и вершина х называется инцидентной такой дуге а.

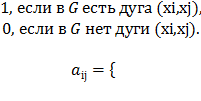       Матрица смежности А = [a_ij] орграфа G(Х, А) с n вершинами имеет размерность nхn и определяется следующим образом:

Матрица смежности для орграфа изображенного на рис. 1.1. представлена на рис. 1.3.

 

 

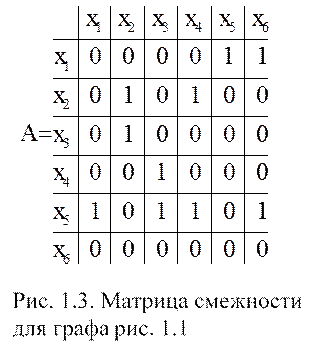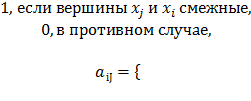Для неориентированного графа матрица смежности определяется так:

т.е. матрица смежности неориентированного графа всегда симметрична. Матрица смежности графа рис. 1.2. представлена на рис. 1.5.

Матрица инциденций В = [bij]  орграфа G(Х, А) с n вершинами и m дугами имеет размерность n x m и определяется так:

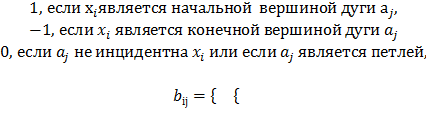
Матрица инциденций для графа рис. 1.1. представлена на рис. 1.4. Для неориентированного графа матрица инциденций составляется также, как и для орграфа, только все элементы, равные –1, заменяются на +1. Для графа рис.1.2. матрица инциденций приведена на рис. 1.6.

Степень d вершины x_i  неориентированного графа есть число ребер, инцидентных этой вершине. Для графа рис. 1.2.

d(x₁) = d(x₂) = d(x₃) = d(x₄) = 3;  d(x₅) = 4.

В ориентированном графе степень вершины хi характеризуется двумя числами: полустепенью исхода, равной числу дуг, исходящих из хi, и полустепенью захода, равной числу дуг, входящих в хi.

Упражнения

1.1. Чему равна сумма элементов i-й строки в матрице смежности орграфа , i – го столбца(

1.2.  Изменится ли матрица смежности орграфа, если пренебречь ориентацией дуг(

1.3. В матрице инциденций неориентированного графа: что представляет собой сумма элементов i-ой  строки, i-го столбца(

1.4. Неориентированный  граф  G(X, A) задан матрицей смежности А:

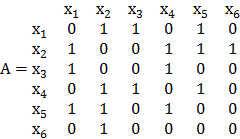Привести геометрическое и аналитическое представление графа, построить матрицу инциденций.

1.5. Чему равна сумма степеней всех вершин неориентированного графа(