1.6. Что определяет сумма полустепеней исхода всех вершин орграфа, сумма полустепеней захода(
1.7. Доказать, что в неориентированном графе число вершин с нечетной степенью четно (нуль – четное число).
1.8. Можно ли из полного графа с 17 вершинами удалить некоторые ребра так, чтобы степень каждой вершины равнялась пяти(
2.Части графов
Граф G((X,( A() называется частью графа G(X, A), если Х( ( Х, А.
Рассмотрим два вида частей: подграф (или порожденый подграф) и суграф (или остовный подграф).
Подграфом Gs графа G(Х, Г) называется граф (Хs, Гs), в который входит лишь часть вершин графа G, образующих множество Хs, вместе с дугами, соединяющими эти вершины, т.е. Хs ( Х и для каждой вершины хi ( Хs Гs(хi) = Г(хi) ( Хs
Граф на рис. 2.1. (б) – подграф графа G, изображенного на рис. 2.1, (а).

Суграфом Gр графа (Х, А) называется граф (Х, Ар ) в котором Ар ( А, т.е. суграф содержит то же самое множество вершин, что и исходный граф G, а множество дуг суграфа является подмножеством множества дуг исходного графа. Суграф Gр графа G приведен на рис. 2.1. (в).
Для любой части G1 графа G существует единственная дополнитель-ная часть – дополнение (G1, состоящее из всех ребер графа G которые не принадлежат G1.
Дополнение (Gs к подграфу Gs приведено на рис. 2.1.(г), дополнение (Gр к суграфу Gр – на рис. 2.1. (д).
Упражнения
2.1. Для неориентированного графа с шестью вершинами привести примеры подгафов, суграфов и их дополнений.
3. Характеристики связности
В ориентированном графе к таким характеристикам относятся путь и контур.
Путем ( ориентированного графа называется последовательность дуг, в которой окончание каждой предыдущей дуги совпадает с началом следующей. Одна и та же дуга в пути может встречаться несколько раз. Если начальная вершина первой дуги в пути хi, а конечная вершина последней дуги хj, то путь обозначают как ( (xi, xj).
 Примеры путей для графа на рис. 3.1.
Примеры путей для графа на рис. 3.1.
( (х2, х6) = (а4, а10, а8, а7, а9) (а)
( (х1, х3) = (а1, а4, а10, а8,) (б)
( (х1, х6) = (а1, а4, а10, а8, а5, а4, а9) (в)
Иногда путь удобно представить в виде последовательности вершин, например, путь (а): ( (х2, х6) = (х2, х5, х4, х3, х5, х6).
Путь называется простым, если в нем каждая дуга встречается только один раз, т.е. дуги не повторяются. Например, приведенные выше пути (а) и (б) являются простыми, так как дуга а4 используется в нем дважды.
Путь называется элементарным, если он не содержит повторяющихся вершин (путь (б) в графе на рис. 3.1.).Длиной пути l(() называется количество дуг, составляющих этот путь. Так, для графа рис. 3.1. l(((х(, х((( ( (, l(((х1, х3(( ( 4, l(((х1, х((( ( 7.
Если каждой дуге орграфа (xi, xj) приписано какое-то число (вес) сij, означающее параметрическую характеристику (стоимость, надежность, время и т.д.), то граф называется графом со взвешенными дугами. Если число приписано вершинам графа, то граф называется графом со взвешенными вершинами. Если числа (веса) приписаны и дугам , и вершинам, то граф становится взвешенным. Длина пути в графе со взвешенными дугами равна сумме длин (весов) всех дуг, входящих в путь, причем каждая дуга рассматривается столько раз, сколько она встречается в пути:
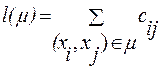 |
Контуром в орграфе называется замкнутый элементарный путь, т.е. путь, в котором начальная и конечная вершины совпадают. В графе на рис. 3.1. пути (а4, а10, а8, а5), (а7, а10, а8) – контуры.
В неориентированном графе существуют понятия цепи и цикла, аналогичные понятиям, соответственно, пути и контура в орграфе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.