Прогноз развития транспортных средств лесопромышленного предприятия. Оптимальные сроки вложения капитальных затрат

Решаем поставленную задачу:

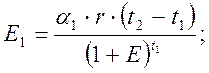
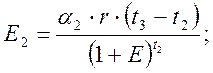
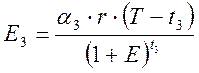     при E= 0,1;

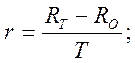
Подставив в формулу и проведя необходимые преобразования, получаем уравнение:

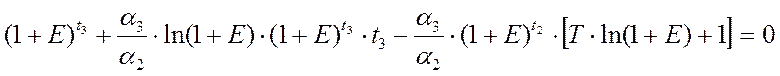
Уравнение также может быть представлено в следующем виде:

;

Решением этого уравнения является точка пересечения графика функции:

 и   ;

;

;

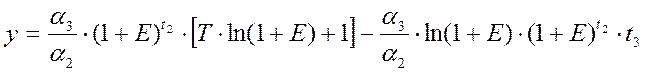Подставляя данные в уравнение, получаем при:

t₂ = 2;

y(1) = 8,37 – 0,14t₃;

t3	10	40
y(1)	6,97	2,77

t₂ = 5;

y(2) = 11,14 – 0,165t₃;

t3	10	40
y(2)	9,49	4,54

t₂ = 10;

y(3) = 17,95 – 0,266t₃;

t3	10	40
y(3)	15,29	7,31

t₂ = 12;

y(4) = 21,72 – 0,32t₃;

t3	10	40
y(4)	18,52	8,92

t₂ = 15;

y(5) = 28,9 – 0,43t₃;

t3	10	40
y(5)	24,6	11,7

t₂ = 18;

y(6) = 38,49 – 0,57t₃;

t3	10	40
y(6)	32,79	15,69

По полученным расчётным данным строим 6 прямых:

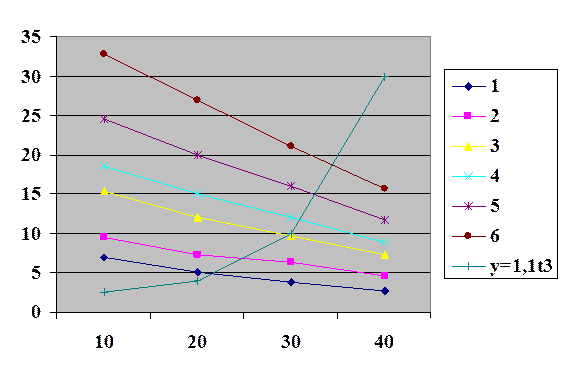
В точках пересечения получаем значения t, подставляем в формулу и определяем оптимальные затраты.

1		2		3		4		5		6
E1	0	E1	26,03	E1	69,42	E1	86,78	E1	112,81	E1	138,84
E2	245,87	E2	195,59	E2	107,94	E2	89,23	E2	62,85	E2	47,22
E3	106,44	E3	63,32	E3	44,29	E3	32,04	E3	24,07	E3	15,37
Σ	352,31	Σ	284,94	Σ	221,65	Σ	208,05	Σ	199,73	Σ	201,43

(1)  

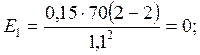
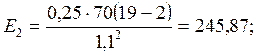
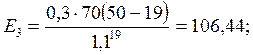
(2)  

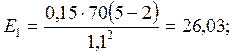
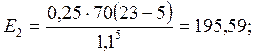
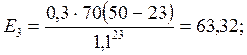
(3)  

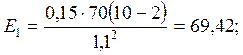
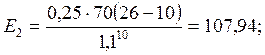
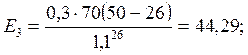
(4)  

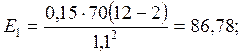
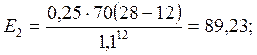
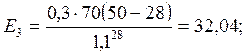
(5)  

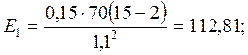
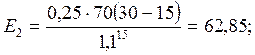
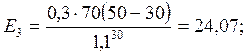
(6)  

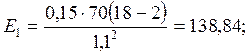
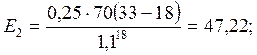
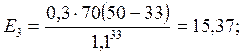
Вывод: в пятом рассмотренном варианте сумма затрат минимальна, следовательно оптимальные сроки вложения капитальных затрат обеспечиваются пятым вариантом.