ВАРИАНТ 9
Лабораторная работа №2. 3
1. Постановка задачи. 3
2. Решение с помощью графов на максимум и на минимум.. 3
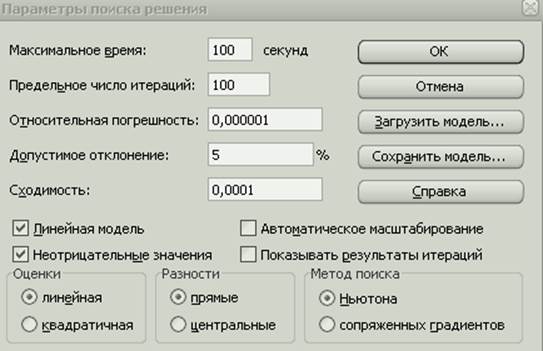
3. Решение в EXEL (с помощью поиска решений) 8
Лабораторная работа №3. 10
1. Постановка задачи. 10
2. План раскроя. 10
3. Математическая модель. 11
4. Решение в маткаде. 12
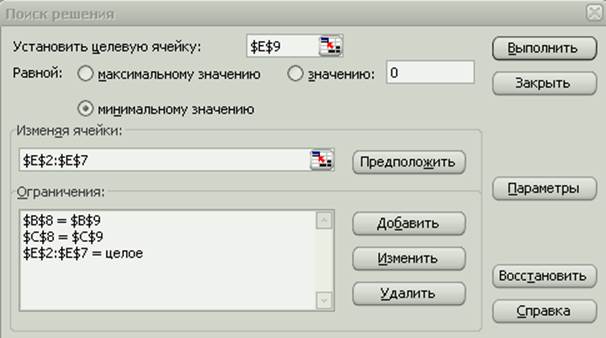
5. Решение в экселе (поиск решений) 13
Лабораторная работа №6. 16
1. Постановка задачи. 16
2. Построение матрицы W... 16
4. Строим график ганта. 19
5. Решение задачи «Поиском решения» в MS Excel 19
6. Решение задачи методом перебора с возвратом в MathCAD.. 23
Цель работы. Овладение навыками разработки математической модели и решение задачи оптимизации оснащения магазина обрабатывающего центра с помощью теории графов.
Постановка задачи. Имеется n различных видов инструментов для оснащения магазина обрабатывающего центра, причем число инструментов каждого вида можно считать неограниченным.
Известно, что каждый инструмент i-го вида занимает ai гнезд обрабатывающего центра и время его переточки равно ci .
После установки по одному инструменту каждого вида осталось b свободных гнезд обрабатывающего центра.
Необходимо оснастить оставшуюся свободной части магазина таким образом, чтобы суммарное время работы инструментов было максимальным (минимальным).
Число свободных гнезд магазина обрабатывающего центра равно 7.
Вариант №9.
|
Инструменты |
1 |
2 |
3 |
4 |
5 |
6 |
|
Стойкость |
2 |
7 |
6 |
2 |
8 |
5 |
|
Число гнезд |
4 |
4 |
3 |
1 |
5 |
2 |
Решим задачу с помощью алгоритма ДЛИННЕЙШИЙ ПУТЬ
Рассмотрим задачу, математическая модель которой:
max: z=2x1+7x2+6x3+2x4+8x5+5x6
4x1+4x2+3x3+x4+5x5+2x6=7
Приведем задачу
Исключаем x1, так как a[1]=a[2]=4 и c[1]=2<7=c[2]
Таким образом приведенная задача имеет вид:
max: z=7x2+6x3+2x4+8x5+5x6
4x2+3x3+x4+5x5+2x6=7
Для вершины 0:
0->1, 1-0=1=a4, c4=2
0->2, 2-0=2=a6, c6=5
0->3, 3-0=3=a3, c3=6
0->4, 4-0=4=a2, c2=7
0->5, 5-0=5=a5, c5=8
Для вершины 1:
1->2, 2-1=1=a4, c4=2
1->3, 3-1=2=a6, c6=5
1->4, 4-1=3=a3, c3=6
1->5, 5-1=4=a2, c2=7
1->6, 6-1=5=a5, c5=8
Для вершины 2:
2->3, 3-2=1=a4, c4=2
2->4, 4-2=2=a6, c6=5
2->5, 5-2=3=a3, c3=6
2->6, 6-2=4=a2, c2=7
2->7, 7-2=5=a5, c5=8
Для вершины 3:
3->4, 4-3=1=a4, c4=2
3->5, 5-3=2=a6, c6=5
3->6, 6-3=3=a3, c3=6
3->7, 7-3=4=a2, c2=7
Для вершины 4:
4->5, 5-4=1=a4, c4=2
4->6, 6-4=2=a6, c6=5
4->7, 7-4=3=a3, c3=6
Для вершины 5:
5->6, 6-5=1=a4, c4=2
5->7, 7-5=2=a6, c6=5
Для вершины 6:
6->7, 7-6=1=a4, c4=2
Матрица графа:
0 1 2 3 4 5 6 7
0 - 2 5 6 7 8 - 1 - - 2 5 6 7 8 2 - - - 2 5 6 7 8
3 - - - - 2 5 6 7
4 - - - - - 2 5 6
5 - - - - - - 2 5
6 - - - - - - - 2
7 - - - - - - - l0=0, l1=2, l2=5, l3=7, l4=10, l5=12, l6=15, l7=17
xi=7, j=6, l[xi]-l[j]=2=l(j,xi)=2 добавляем 6
xi=6, j=4, l[xi]-l[j]=5=l(j,xi)=5 добавляем 4
xi=4, j=2, l[xi]-l[j]=5=l(j,xi)=5 добавляем 2
xi=2, j=0, l[xi]-l[j]=5=l(j,xi)=5 добавляем 0
Путь: 0-2-4-6-7
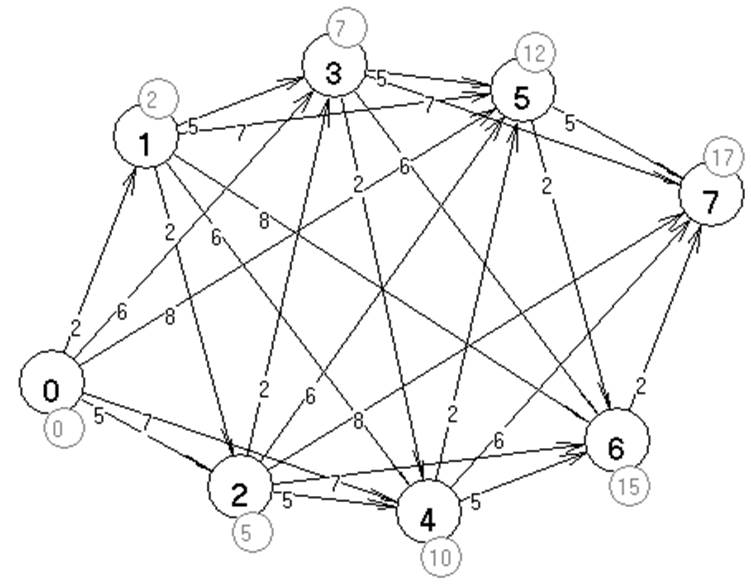
На рисунке представлен граф с длиннейшим путем. Ему соответствует решение задачи:
x*1=0, x*2=0, x*3=0, x*4=1, x*5=0, x*6=3, Zmax=17
Решим задачу с помощью алгоритма КРАТЧАЙШИЙ ПУТЬ
Рассмотрим задачу, математическая модель которой:
min: z=2x1+7x2+6x3+2x4+8x5+5x6
4x1+4x2+3x3+x4+5x5+2x6=7
Приведем задачу
Исключаем x2, так как a[1]=a[2]=4 и c[1]=2<7=c[2]
Таким образом приведенная задача имеет вид:
min: z=2x1+6x3+2x4+8x5+5x6
4x1+3x3+x4+5x5+2x6=7
Для вершины 7:
7->6, 6-7=1=a4, c4=2
7->5, 5-7=2=a6, c6=5
7->4, 4-7=3=a3, c3=6
7->3, 3-7=4=a1, c1=2
7->2, 2-7=5=a5, c5=8
Для вершины 6:
6->5, 5-6=1=a4, c4=2
6->4, 4-6=2=a6, c6=5
6->3, 3-6=3=a3, c3=6
6->2, 2-6=4=a1, c1=2
6->1, 1-6=5=a5, c5=8
Для вершины 5:
5->4, 4-5=1=a4, c4=2
5->3, 3-5=2=a6, c6=5
5->2, 2-5=3=a3, c3=6
5->1, 1-5=4=a1, c1=2
5->0, 0-5=5=a5, c5=8
Для вершины 4:
4->3, 3-4=1=a4, c4=2
4->2, 2-4=2=a6, c6=5
4->1, 1-4=3=a3, c3=6
4->0, 0-4=4=a1, c1=2
Для вершины 3:
3->2, 2-3=1=a4, c4=2
3->1, 1-3=2=a6, c6=5
3->0, 0-3=3=a3, c3=6
Для вершины 2:
2->1, 1-2=1=a4, c4=2
2->0, 0-2=2=a6, c6=5
Для вершины 1:
1->0, 0-1=1=a4, c4=2
Матрица графа:
0 1 2 3 4 5 6 7
0 - - - - - - - 1 2 - - - - - - 2 5 2 - - - - - 3 6 5 2 - - - - 4 2 6 5 2 - - - 5 8 2 6 5 2 - - 6 - 8 2 6 5 2 - 7 - - 8 2 6 5 2 l0=8, l1=6, l2=4, l3=2, l4=6, l5=4, l6=2, l7=0
xi=0, j=1, l[xi]-l[j]=2=l(j,xi)=2 добавляем 1
xi=1, j=2, l[xi]-l[j]=2=l(j,xi)=2 добавляем 2
xi=2, j=3, l[xi]-l[j]=2=l(j,xi)=2 добавляем 3
xi=3, j=7, l[xi]-l[j]=2=l(j,xi)=2 добавляем 7
Путь: 0-1-2-3-7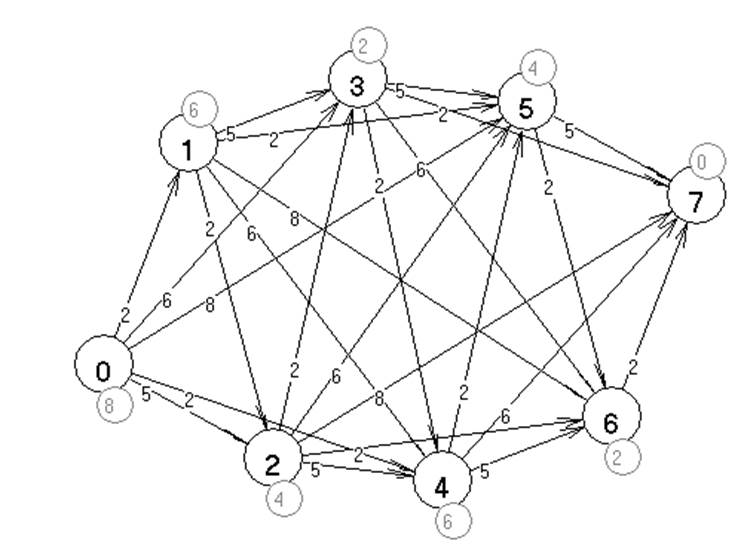
На рисунке представлен граф с кратчайшим путем. Ему соответствует решение задачи:
x*1=1, x*2=0, x*3=0, x*4=3, x*5=0, x*6=0, Zmin=8
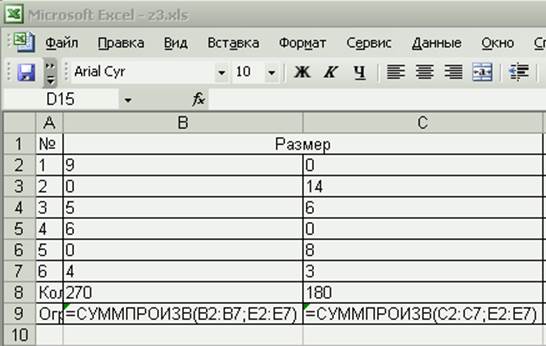
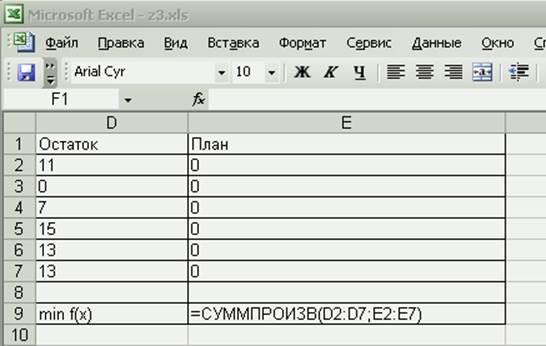
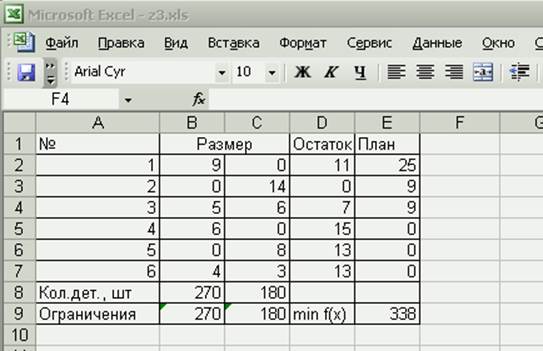
Составим таблицу:
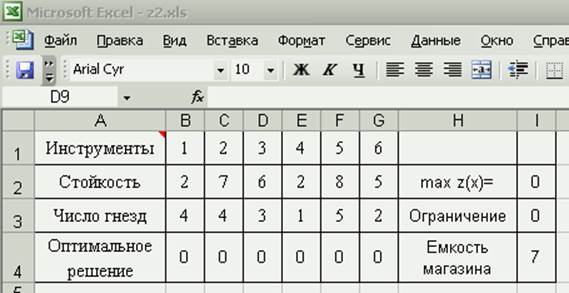
В режиме проверки формул имеем:
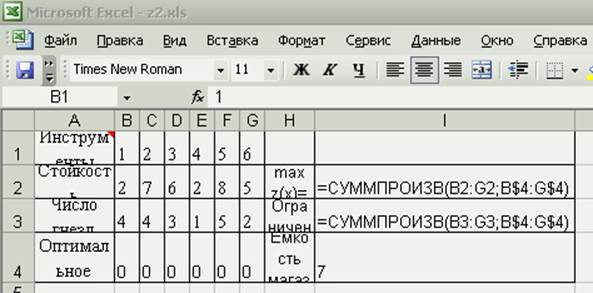
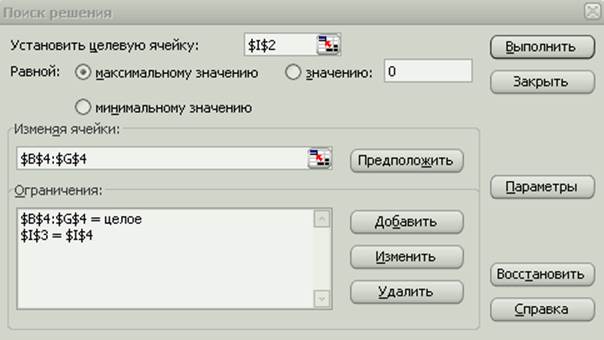
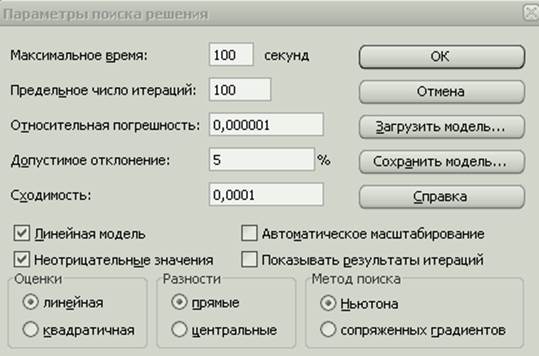

Цель работы. Овладение навыками использования метода линейного программирования для решения технологических задач.
Постановка задачи. Из листового проката двух (одного) типа необходимо вырезать некоторое количество заготовок для производства 90 штук изделий с минимальными отходами. Для одного изделия требуется деталей первого типа – 3 штуки, второго – 2, третьего (если это предусмотрено в варианте задания) – 1. Возможности заготовительного участка не ограничены. При решении задачи разработать не менее трех вариантов раскроя для каждого из двух типов листового проката или не менее шести, если прокат только одного типа.
Дано:
Деталь Д Деталь И
Деталь И
Количество полотен: 2
1) a=4, b=14
2) a=5, b=9
Требуется самостоятельно разработать 6 вариантов раскроя этих деталей. Приведем одним из возможных способов такого раскроя:
Лист 1 по 1 варианту раскроя
Количество деталей Д=9
Остаток=11

Лист 1 по 2 варианту раскроя
Количество деталей И=14
Остаток=0
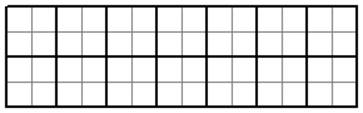
Лист 1 по 3 варианту раскроя
Количество деталей Д=5
Количество деталей И=6
Остаток=7
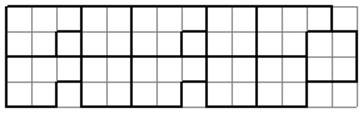
Лист 2 по 1 варианту раскроя
Количество деталей Д=6
Остаток=15
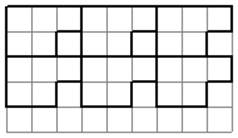
Лист 2 по 2 варианту раскроя
Количество деталей И=8
Остаток=13
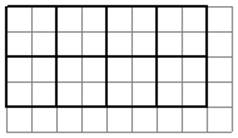
Лист 2 по 3 варианту раскроя
Количество деталей Д=4
Количество деталей И=3
Остаток=13
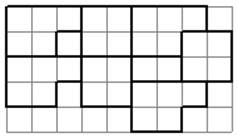
Составим математическую модель данной задачи. Введем следующие обозначения:
х1 – количество листов Лист1 по 1 варианту раскроя;
х2 – количество листов Лист1 по 2 варианту раскроя;
х3 – количество листов Лист1 по 3 варианту раскроя;
х4 – количество листов Лист2 по 1 варианту раскроя;
х5 – количество листов Лист2 по 2 варианту раскроя;
х6 – количество листов Лист2 по 3 варианту раскроя;
Составим целевую функцию, выписав остатки раскроя:
f(x)=11x1+0x2+7x3+15x4+13x5+13x6
Согласно условию задачи, необходимо раскроить 270 штук Детали Д. Проанализировав рисунки раскроя, запишем ограничения для Детали Д:
9x1+0x2+5x3+6x4+0x5+4x6=270
Согласно условию задачи, необходимо раскроить 180 штук Детали И. Проанализировав рисунки раскроя, запишем ограничения для Детали И:
0x1+14x2+6x3+0x4+8x5+3x6=180
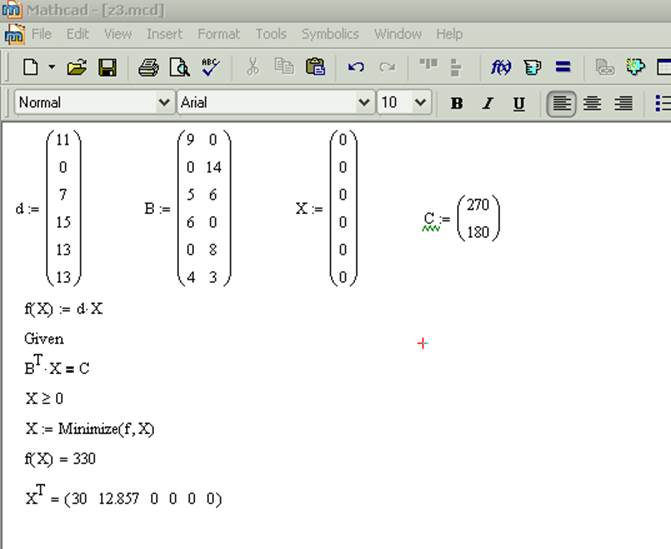
Математическая модель задачи следующая
Минимизировать остатки раскроя:
min: f(x)=11x1+0x2+7x3+15x4+13x5+13x6
при ограничениях:
на план выпуск:
9x1+0x2+5x3+6x4+0x5+4x6=270
0x1+14x2+6x3+0x4+8x5+3x6=180
на целочисленность:
xi - целые, i=1,6
на неотрицательность:
xi >=0, i=1,6

Постановка задачи: На линии горячей обработки, состоящей из 4 станков, нужно обработать 5 различных деталей. Все детали должны проходить вдоль линии в одном направлении через каждый станок. Задана длительность pi,j обработки детали i на j-ом станке. Требуется составить последовательность горячей обработки деталей, позволяющую закончить ее за минимальное время.
i/j 1 2 3 4
1 6 4 11 2
2 7 7 5 8
3 4 9 4 5
4 7 8 8 7
5 11 7 5 11
Для удобства расчетов представим в виде таблицы
Станок1 Станок2 Станок3 Станок4
Деталь1 6 4 11 2
Деталь2 7 7 5 8
Деталь3 4 9 4 5
Деталь4 7 8 8 7
Деталь5 11 7 5 11
1. Решим задачу коммивояжера при помощи алгоритма Литтла.
w1,2=max{6,6+4-7,6+4+11-7-7,6+4+11+2-7-7-5}=max{6,3,7,4}=7
w1,3=max{6,6+4-4,6+4+11-4-9,6+4+11+2-4-9-4}=max{6,6,8,6}=8
w1,4=max{6,6+4-7,6+4+11-7-8,6+4+11+2-7-8-8}=max{6,3,6,0}=6
w1,5=max{6,6+4-11,6+4+11-11-7,6+4+11+2-11-7-5}=max{6,-1,3,0}=6
w2,1=max{7,7+7-6,7+7+5-6-4,7+7+5+8-6-4-11}=max{7,8,9,6}=9
w2,3=max{7,7+7-4,7+7+5-4-9,7+7+5+8-4-9-4}=max{7,10,6,10}=10
w2,4=max{7,7+7-7,7+7+5-7-8,7+7+5+8-7-8-8}=max{7,7,4,4}=7
w2,5=max{7,7+7-11,7+7+5-11-7,7+7+5+8-11-7-5}=max{7,3,1,4}=7
w3,1=max{4,4+9-6,4+9+4-6-4,4+9+4+5-6-4-11}=max{4,7,7,1}=7
w3,2=max{4,4+9-7,4+9+4-7-7,4+9+4+5-7-7-5}=max{4,6,3,3}=6
w3,4=max{4,4+9-7,4+9+4-7-8,4+9+4+5-7-8-8}=max{4,6,2,-1}=6
w3,5=max{4,4+9-11,4+9+4-11-7,4+9+4+5-11-7-5}=max{4,2,-1,-1}=4
w4,1=max{7,7+8-6,7+8+8-6-4,7+8+8+7-6-4-11}=max{7,9,13,9}=13
w4,2=max{7,7+8-7,7+8+8-7-7,7+8+8+7-7-7-5}=max{7,8,9,11}=11
w4,3=max{7,7+8-4,7+8+8-4-9,7+8+8+7-4-9-4}=max{7,11,10,13}=13
w4,5=max{7,7+8-11,7+8+8-11-7,7+8+8+7-11-7-5}=max{7,4,5,7}=7
w5,1=max{11,11+7-6,11+7+5-6-4,11+7+5+11-6-4-11}=max{11,12,13,13}=13
w5,2=max{11,11+7-7,11+7+5-7-7,11+7+5+11-7-7-5}=max{11,11,9,15}=15
w5,3=max{11,11+7-4,11+7+5-4-9,11+7+5+11-4-9-4}=max{11,14,10,17}=17
w5,4=max{11,11+7-7,11+7+5-7-8,11+7+5+11-7-8-8}=max{11,11,8,11}=11
i/j 1 2 3 4 5 6
1 ∞ 7 8 6 6 23
2 9 ∞ 10 7 7 27
3 7 6 ∞ 6 4 22
4 13 11 13 ∞ 7 30
5 13 15 17 11 ∞ 34
6 0 0 0 0 0 ∞
2. Решим задачу коммивояжера методом "Ближайшего соседа".
1-4-5-2-3-6-1 -> f(x1)=6+7+15+10+22+0=60
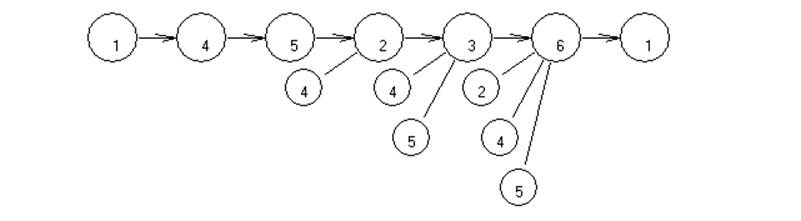
2-4-5-1-3-6-2 -> f(x2)=7+7+13+8+22+0=57
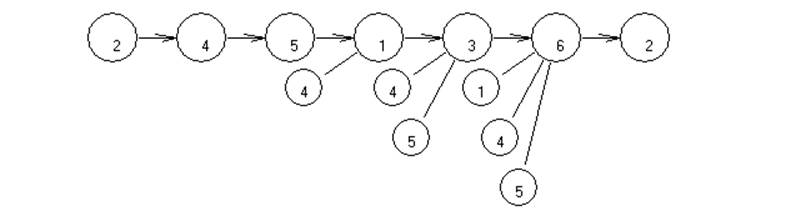
3-5-4-2-1-6-3 -> f(x3)=4+11+11+9+23+0=58
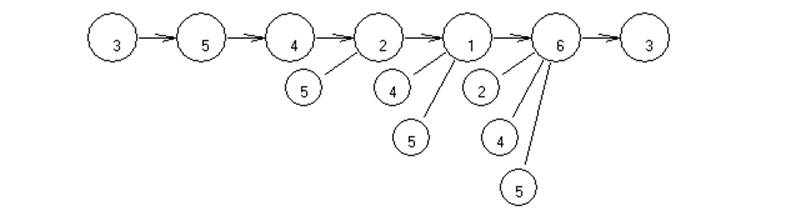
4-5-1-2-3-6-4 -> f(x4)=7+13+7+10+22+0=59
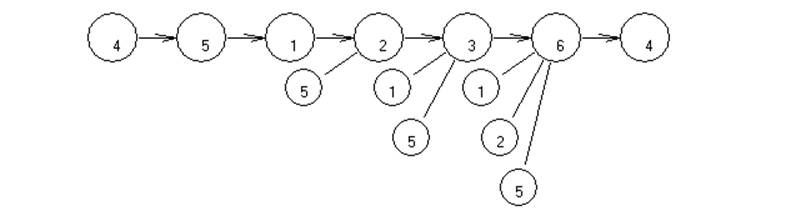
5-4-2-1-3-6-5 -> f(x5)=11+11+9+8+22+0=61
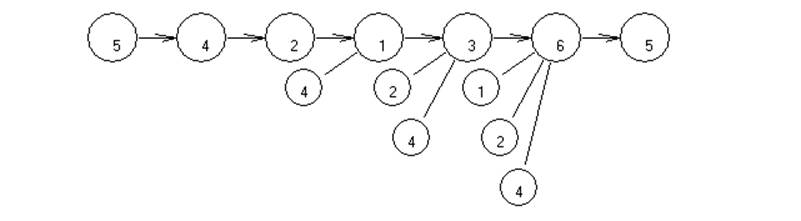
6-1-4-5-2-3-6 -> f(x6)=0+6+7+15+10+22=60
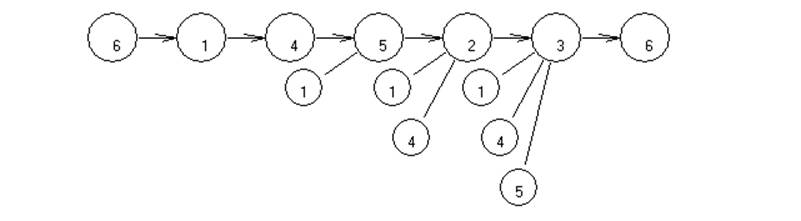
Полученное решение - 2-4-5-1-3-6-2 -> f(x2)=7+7+13+8+22+0=57
Точное (алгоритмом Литтла) и приближенное (методом "Ближайших соседей") решения могут не совпадать.
В действительности при n<40, ошибка приближенного метода может быть
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.