Теплопроводность. Закон Фурье. Дифференциальное уравнение теплопроводности

Значение d₂, соответствующее минимальному полному термическому сопротивлению теплопередачи, называется критическим диаметром и обозначается d_кр.

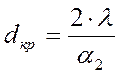
При  d_кр > d₂ с увеличением d₂, R_l снижается, так как увеличение наружной поверхности оказывает на R_l большее влияние, чем увеличение толщины стенки.

При d_кр < d₂  с увеличением d₂, R_l возрастает, так как здесь имеет место доминирующее влияние толщины стенки.

Это необходимо учитывать при выборе тепловой изоляции труб и цилиндров аппаратов.

Рассмотрим d_кр изоляции, наложенной на трубу.

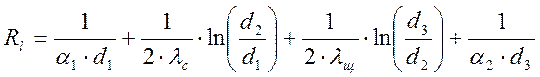
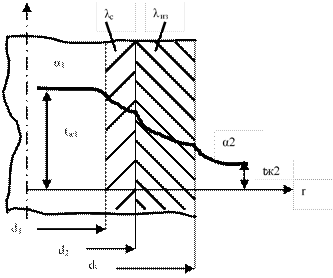
Из уравнения 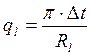  следует , что q_l при увеличении d₃  сначала будет возрастать и при d₃ = d_кр будет иметь max q_l.  При дальнейшем увеличении внешнего диаметра d₃ изоляции q_l  будет снижаться. Выбрав какой – либо теплоизоляционный материал прежде всего нужно рассчитать d_кр для заданных λ_из и α₂.

Если окажется, что величина d_кр > d₂, то применение выбранного материала в качестве изоляции нецелесообразно. В области d₂< d₃< d_кр.из. при увеличении толщины изоляции будет наблюдаться увеличение теплопотерь.

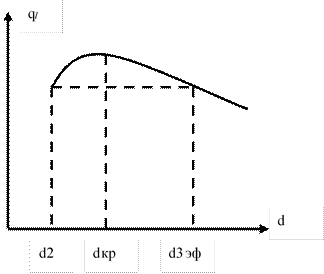
Только при d₃ = d_{3 эф} тепловые потери вновь станут такими же, как для первоначального, неизолированного трубопровода. Следовательно, некоторый слой тепловой изоляции не будет оправдывать своего назначения.

Следовательно, для эффективной работы тепловой изоляции необходимо, чтобы d_кр.щ. ≤ d₂.

9. Теплопроводность в стержне (ребре) постоянного поперечного сечения.

Рассмотрим распространение тепла в прямом стержне с постоянным поперечным сечением по длине.

f- площадь поперечного сечения стержня.

U- периметр

- температура среды

- для всей поверхности

λ- стержня достаточно велик, а поперечное сечение мало по сравнению с его длиной.

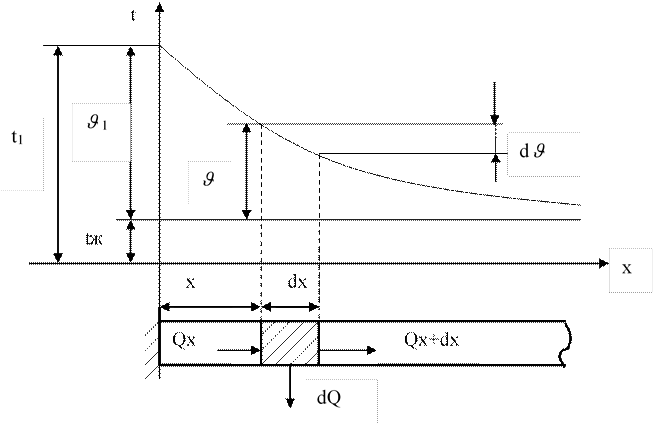
Это дает основание пренебрегать изменением температуры в поперечном сечении и считать, что она распространяется вдоль оси стержня. Отсчет температуры будем вести от

.

Избыточная температура стержня

 

t -  текущая температура стержня.

Если задана температура основания стержня t₁, то избыточная температура стержня будет:

Уравнение теплового баланса для выделенного элемента стержня:

dQ -  количество теплоты, отдаваемое за единицу времени наружной поверхностью элемента окружающей его среде.

Согласно з.Фурье

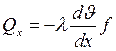
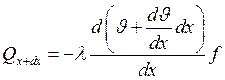 , откуда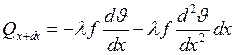                                                 

следовательно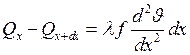                    

Но согласно ф. Н.-Рихмана

приравнивая получим:

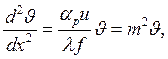 где m, 1/м.

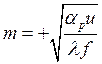
Из этого выражения видно, что для ребра, форма и размеры которого заданы, при условии  по всей поверхности и постоянстве λ в рассматриваемом интервале температур, m=const , тогда общий интервал для уравнения будет:

С₁ и С₂ - определяются из граничных условий

Стержень бесконечной длинны:

При  x=0  t=t₁  и  υ=υ_{1 .}Если l→∞, то вся теплота, подводимая к стержню, будет отдана им в окружающую среду  и при x→∞ имеем υ=0.

при x=0   υ₁=C₁+C₂

при x→∞  С₁×e^∞=0   -  это возможно, только при C₁=0.  Таким образом C₂=υ₁

Получим υ=υ₁e^-mx

Тогда можно записать: 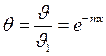  – безразмер.t-ра

 

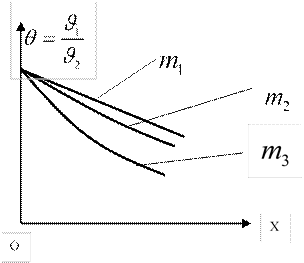
При оребрении нужно выбирать материал ребер с большим λ. Это приводит к уменьшению mи сохранении больших избыточных температур вдоль стержня. При 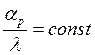 значении mвозрастают с возрастанием , что указывает на более эффективную работу рёбер с профилями, имеющими меньшее отношение  при этом же конечном сечении.

Количество теплоты, отданной стержнем в окружающую среду:

Стержень конечной длинны:

При     x=0         υ=υ₁ 

При     x=l 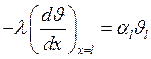      или  

 - температура на конце стержня,  - коэффициент т/от с торца стержня;

Решение даёт:

Если теплоотдачей с конца стержня пренебречь, то:

При     x=0        υ=υ₁

При   x=l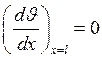        

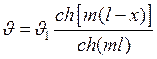
Количество теплоты, Q_p, Вт, отдаваемое поверхностью ребра в окружающую среду будет равно количеству теплоты, подводимому к основанию ребра

Если длинна стержня очень велика, ch(ml)→∞, а th(ml)≈1, тогда =0 и формула превращается в формулу для определения Q для ∞ длинного стержня.

10. Теплопередача через ребристую плоскую стенку

Необходимо найти тепловой поток через плоскую ребристую стенку безграничных размеров. Стенка оребрена со стороны меньшего коэффициента теплоотдачи.

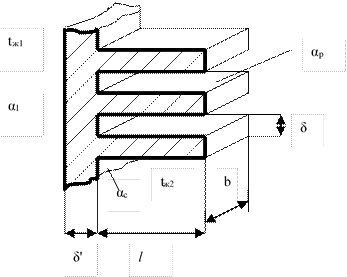
Поскольку для ребра b»δ, то периметр полученного сечения ребер