










удельная поверхность теплопередачи; ![]() - температура
охлаждающей воды;
- температура
охлаждающей воды; ![]() - коэффициент
теплопередачи.
- коэффициент
теплопередачи.
В системе
уравнений (12.48) не учитывается масса зародышей в силу их
малости. Однако зародышеобразование можно учесть в граничном условии для
функции ![]() .
Соотношение для функции плотности распределения
.
Соотношение для функции плотности распределения ![]() в точке
в точке ![]() выводится из следующих соображений: за промежуток времени
выводится из следующих соображений: за промежуток времени ![]() в системе возникает
в системе возникает ![]() частиц нулевого размера, которые за
рассматриваемый промежуток времени заполняют (в результате роста) интервал (
частиц нулевого размера, которые за
рассматриваемый промежуток времени заполняют (в результате роста) интервал (![]() ,
,![]() ). С другой стороны, число частиц
в этом же интервале размеров равно
). С другой стороны, число частиц
в этом же интервале размеров равно ![]() . Следовательно,
. Следовательно,
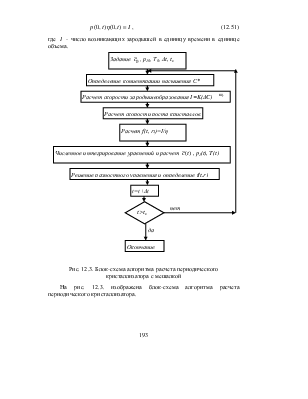
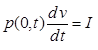 , (12.50)
, (12.50)
или
![]() , (12.51)
, (12.51)
где ![]() -
число возникающих зародышей в единицу времени в единице объема.
-
число возникающих зародышей в единицу времени в единице объема.
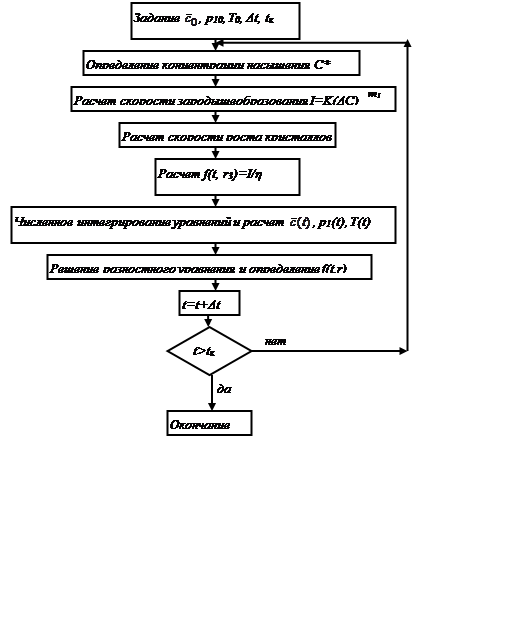 Рис. 12.3.
Блок-схема алгоритма расчета периодического
кристаллизатора с мешалкой
Рис. 12.3.
Блок-схема алгоритма расчета периодического
кристаллизатора с мешалкой
На рис. 12.3. изображена блок-схема алгоритма расчета периодического кристаллизатора.
Так же как и в предыдущем случае, предполагается, что в аппарате происходит идеальное перемешивание частиц потока.
Интегрируя по объему аппарата, занятого смесью, систему уравнений математической модели процесса кристаллизации (12.25) - (12.33), (12.36), (12.38), (12.40), при принятых допущениях получим
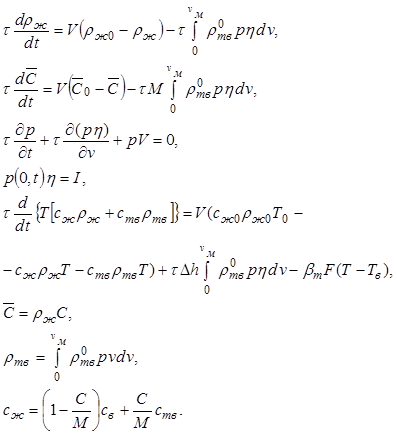 (12.52)
(12.52)
Здесь ![]() -
объем аппарата;
-
объем аппарата; ![]() - объемная
скорость потока;
- объемная
скорость потока; ![]() ,
, ![]() ,
, ![]() -
концентрация, плотность и температура раствора на входе в аппарат.
-
концентрация, плотность и температура раствора на входе в аппарат.
Первые три уравнения в системе (12.52) получаются интегрированием дифференциальных уравнений сохранения массы по объему аппарата. Пятое уравнение (баланса теплоты) получено следующим образом. Сложим три уравнения энергии (12.36), (12.38), (12.40):
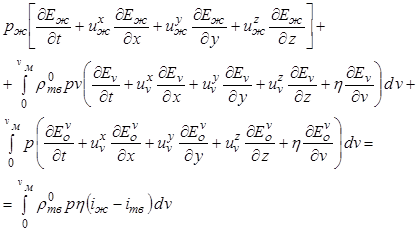 . (12.53)
. (12.53)
Прибавляя и вычитая из уравнения (12.53) выражение
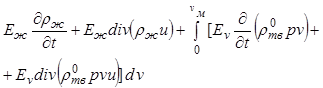 , (12.54)
, (12.54)
получим
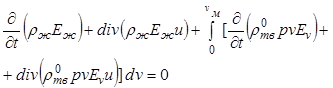 . (12.55)
. (12.55)
Используя уравнения состояния
![]() , (12.56)
, (12.56)
![]() , (12.57)
, (12.57)
уравнение (12.55) приведем к виду
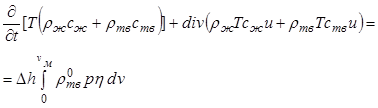 . (12.58)
. (12.58)
Интегрируя уравнение (12.58) по объему, получим пятое уравнение в системе (12.52).
Для установившегося режима работы аппарата система уравнений (12.52) преобразуется к виду
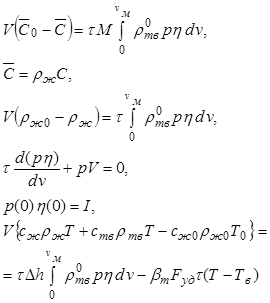 . (12.59)
. (12.59)
Решение последней системы уравнений может быть проведено по следующему алгоритму.
1.
Задают ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
2.
Оценивают величины пересыщения ![]() скорости зародышеобразования
скорости зародышеобразования ![]() и скорости
роста кристаллов
и скорости
роста кристаллов ![]() .
.
3.
Рассчитывают ![]() .
.
4.
Интегрируют
дифференциальное уравнение и рассчитывают ![]() .
.
5.
Определяют ![]() ,
,
![]() ,
, ![]() .
.
6.
Если ![]() и
и ![]() , то расчет оканчивают. В противном случае переходят к пункту
2 при
, то расчет оканчивают. В противном случае переходят к пункту
2 при ![]() и
и ![]() .
.
Кристаллизаторы рассматриваемого типа
включают две зоны: зону роста кристаллов, где кристаллическая фаза образует
взвешенный слой, и зону пересыщения раствора. Обе зоны связаны между собой
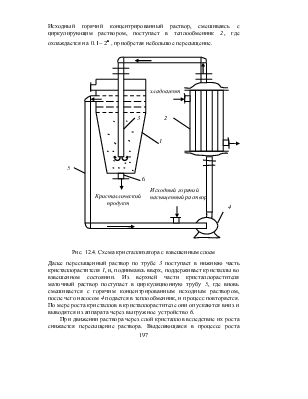
контуром циркуляции раствора. На рис. 12.4. приведена схема кристаллизатора.
Исходный горячий концентрированный раствор, смешиваясь с циркулирующим
раствором, поступает в теплообменник 2, где охлаждается на ![]() , приобретая небольшое пересыщение.
, приобретая небольшое пересыщение.
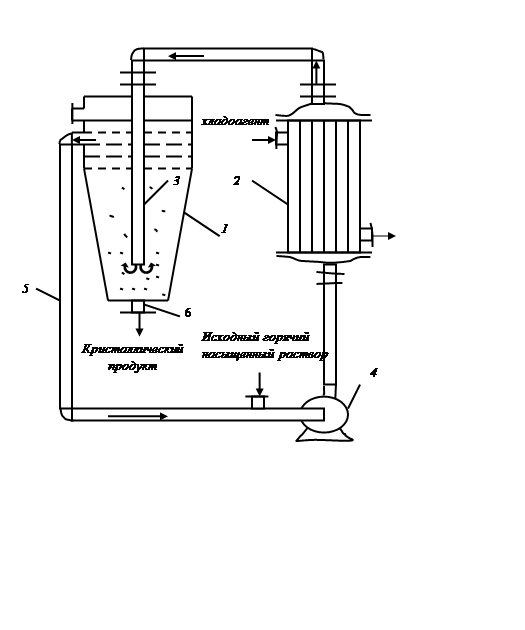 Рис.
12.4. Схема кристаллизатора с взвешенным
слоем
Рис.
12.4. Схема кристаллизатора с взвешенным
слоем
Далее пересыщенный раствор по трубе 3 поступает в нижнюю часть кристаллорастителя 1, и, поднимаясь вверх, поддерживает кристаллы во взвешенном состоянии. Из верхней части кристаллорастителя маточный раствор поступает в циркуляционную трубу 5, где вновь смешивается с горячим концентрированным исходным раствором, после чего насосом 4 подается в теплообменник, и процесс повторяется. По мере роста кристаллов в кристаллорастителе они опускаются вниз и выводятся из аппарата через выгружное устройство 6.
При движении раствора через слой кристаллов вследствие их роста снижается пересыщение раствора. Выделяющаяся в процессе роста кристаллов скрытая теплота кристаллизации увеличивает температуру раствора, что, в свою очередь, приводит к изменению равновесной концентрации раствора.
В дальнейшем будем полагать, что основная масса зародышей возникает в нижней части аппарата, так как здесь создается наибольшее пересыщение раствора и объемная концентрация твердой фазы. Функцией распределения кристаллов по размерам будем пренебрегать, полагая, что в поперечном сечении аппарата кристаллы имеют один и тот же средний размер, Наконец, примем одинаковой вданном сечении аппарата температуру жидкой и кристаллической фаз. При сделанных допущениях общая система уравнений математического описания (12.25) - (12.33), (12.36), (12.38), (12.40) сведется к следующей системе:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
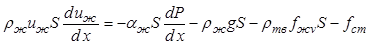 ,
,
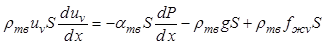 , (12.60)
, (12.60)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
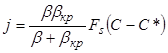 ,
,
![]() ,
,
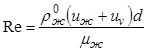 ,
,
![]() .
.
Здесь ![]() -
массовая скорость роста кристаллов в единице объема;
-
массовая скорость роста кристаллов в единице объема; ![]() - массовая скорость роста одного
кристалла;
- массовая скорость роста одного
кристалла; ![]() - масса одного кристалла;
- масса одного кристалла; ![]() - площадь поперечного сечения
аппарата;
- площадь поперечного сечения
аппарата; ![]() - объем кристалла;
- объем кристалла; 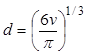 - эквивалентный
диаметр кристалла;
- эквивалентный
диаметр кристалла; ![]() - поверхность одного
кристалла;
- поверхность одного
кристалла; ![]() - равновесная концентрация
раствора;
- равновесная концентрация
раствора; ![]() ,
, ![]() -
теплоемкость жидкой и кристаллической фаз;
-
теплоемкость жидкой и кристаллической фаз; ![]() -
удельная теплота кристаллизации;
-
удельная теплота кристаллизации; ![]() - сила трения
между жидкой фазой и стенками аппарата;
- сила трения
между жидкой фазой и стенками аппарата; ![]() ,
,
![]() - коэффициенты зависимости равновесной концентрации от температуры.
- коэффициенты зависимости равновесной концентрации от температуры.
Запишем граничные условия для системы
уравнений (12.40): при ![]() (нижний конец аппарата):
(нижний конец аппарата):
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , (12.61)
, (12.61)
при ![]() (высота взвешенного слоя):
(высота взвешенного слоя):
![]() . (12.62)
. (12.62)
Рассмотрим уравнения движения жидкой и кристаллической фаз:
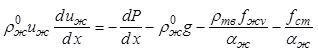 , (12.63)
, (12.63)
![]()
![]() , (12.64)
, (12.64)
Вычитая уравнение (12.64) из (12.63), получим
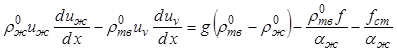 . (12.65)
. (12.65)
Оценка порядка величин членов уравнения (12.65) показывает, что первый, второй и пятый члены являются пренебрежимо малыми по сравнению с третьими четвертым членами. Следовательно, в уравнении (12.65) можно пренебречь всеми членами, кроме третьего и четвертого:
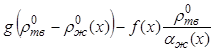 . (12.66)
. (12.66)
Сила взаимодействия между жидкой и твердой
фазами ![]() определяется соотношением
определяется соотношением
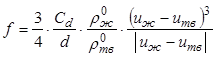 , (12.67)
, (12.67)
где ![]() -
коэффициент сопротивления при стесненном движении кристаллов
-
коэффициент сопротивления при стесненном движении кристаллов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.