Исследование электроприводов переменного тока со скалярным управлением. Типовые блоки в моделях электроприводов переменного тока

Моделирование технических систем. Лабораторная работа №2

Исследование электроприводов переменного тока со скалярным управлением

1. Типовые блоки в моделях электроприводов переменного тока

1.1. Преобразование векторов из двухфазной системы () в трехфазную (А; В; С)

Преобразование производится по следующим соотношениям:

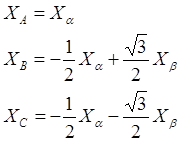                                                                                                         (1)

X – мгновенные значения любых преобразуемых величин (токов, напряжений, потокосцеплений и т.д.)

Структурная схема, реализующая выражения (1), показана на рис. 1.

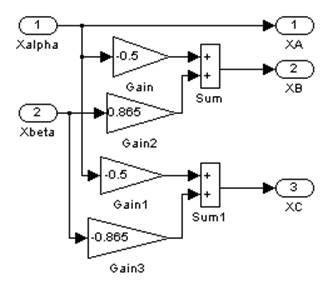
Рис. 1. Структурная схема преобразования 23

1.2. Преобразование векторов из трехфазной системы (А; В; С) в двухфазную ()

Преобразование производится по следующим соотношениям:

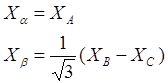                                                                                                            (2)

Структурная схема, реализующая выражения (2), показана на рис. 2.

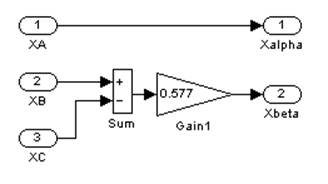
Рис. 2. Структурная схема преобразования 32

1.3. Преобразование координат из неподвижной системы координат (x; y) во вращающуюся систему координат ()

Преобразование производится по следующим соотношениям:

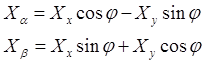,                                                                                                    (3)

где - угол поворота векторов при вращении системы координат со скоростью .

Структурная схема, реализующая выражения (3), показана на рис. 3.

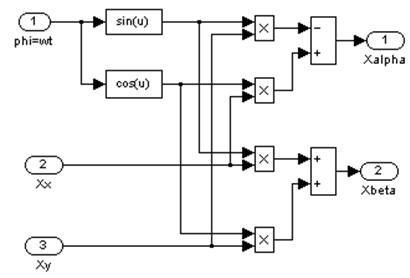
Рис. 3. Структурная схема преобразования (x; y) ()

1.4. Преобразование координат из вращающейся системы координат () в неподвижную систему координат (x; y)

Преобразование производится по следующим соотношениям:

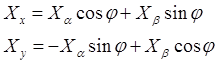                                                                                                  (4)

Структурная схема, реализующая выражения (4), показана на рис. 4.

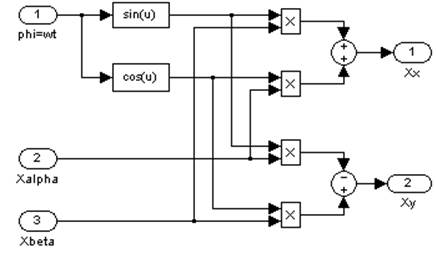
Рис. 4. Структурная схема преобразования ()(x; y)

1.5. Проверка правильности преобразований

Для проверки правильности рассмотрим следующую последовательность преобразований: (А; В; С)()(x; y)()(А; В; С). Модель показана на рис. 5.

Если входные сигналы в данной системе (представляют собой трехфазную систему векторов одинаковой амплитуды, сдвинутые относительно друг друга на 120 градусов) совпадают с выходными, значит, преобразования выполняются корректно.

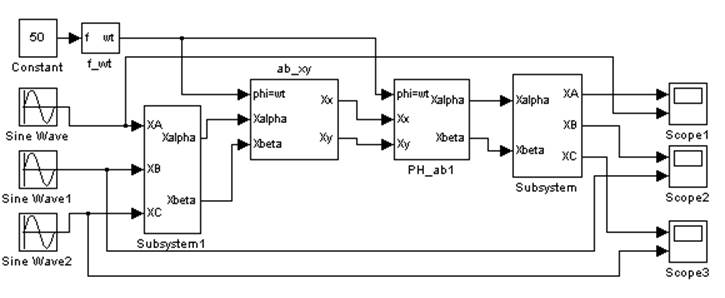
Рис. 5. Структурная схема для проверка правильности преобразований

1.6. Модель асинхронного двигателя

Возможно создание модели двигателя в осях x; y и . То в каких осях создана модель не важно с точки зрения моделирования самого двигателя, т.к. результаты моделирования получаются одинаковыми, но принципиально для создания модели САУ.

На рис. 6 приведена несколько более простая модель в осях . Если ее дополнить преобразованием фаз 3/2 на входе, получится более физичная модель двигателя с трехфазным напряжением на входе, аналогичная модели Simpowersystems.

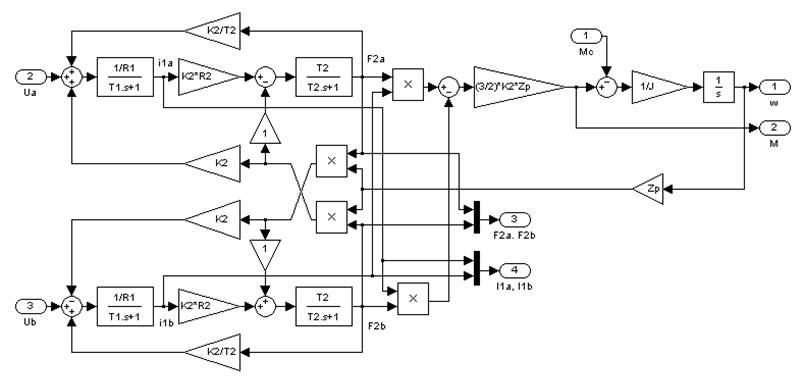
Рис. 6. Модель двигателя в осях

1.8. Модели функциональных преобразователей

Варианты моделей функциональных преобразователей показаны на рис. 7.

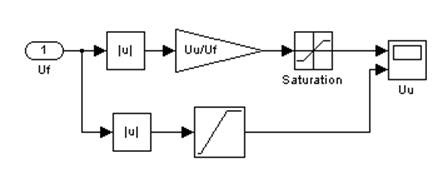
Рис. 7. Модели функциональных преобразователей

Простейшая модель (закон U/f=const) основана на коэффициенте пропорциональности (вычисляемом по номинальным значениям) и блоке ограничения напряжения при частотах выше номинальной.

При необходимости реализации других законов скалярного управления (или при необходимости вводить коррекцию закона U/f=const при малых частотах) можно использовать блок Look-up-table или другие математические блоки.

Наличие блоков вычисления модуля связано с тем, что реверс в подобных моделях реализуется изменением знака частоты. При этом знак напряжения меняться не должен.

1.9. Вычисление угла поворота векторов

На рис. 8 представлены три возможных способа вычисления угла поворота. Первый из них следует считать правильным только при постоянном сигнале задания на частоту. Желательно использовать второй или третий. Второй способ основан на том, что интеграл от угловой скорости вращения вектора является его углом поворота. Другими словами, интегрирование w соответствует ее умножению на время t. При этом возможно в соответствии со способом 3 периодически сбрасывать интегратор с целью уменьшения погрешностей моделирования, что, однако, не является обязательным.

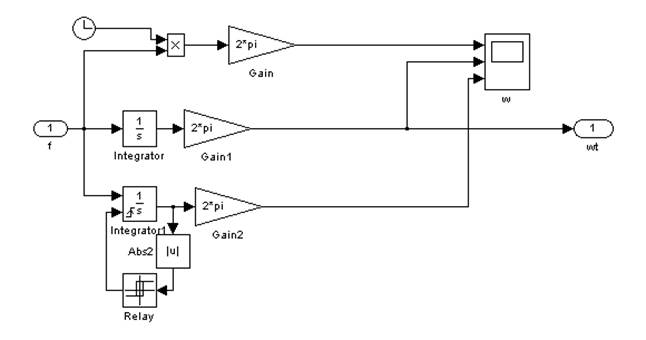
Рис. 8. Вычисление угла поворота

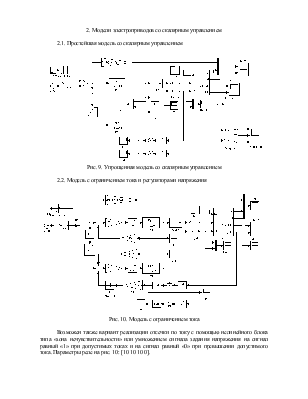
2. Модели электроприводов со скалярным управлением

2.1. Простейшая модель со скалярным управлением

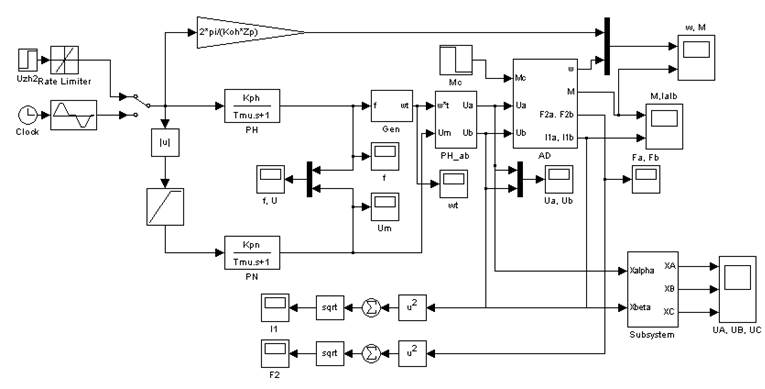
Рис. 9. Упрощенная модель со скалярным управлением

2.2. Модель с ограничением тока и регуляторами напряжения

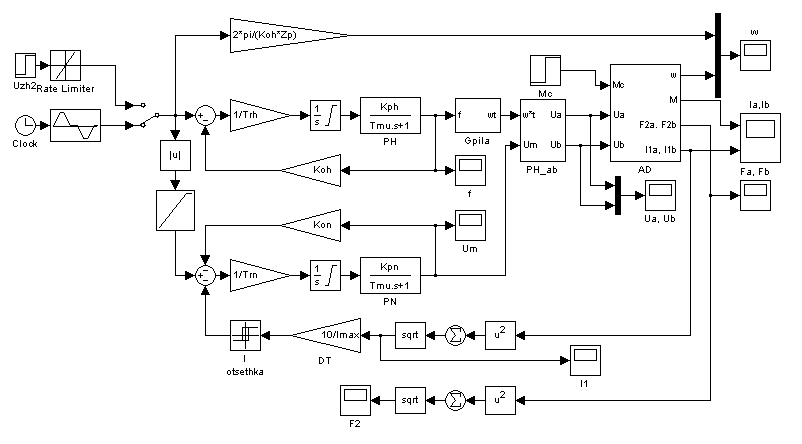
Рис. 10. Модель с ограничением тока

Возможен также вариант реализации отсечки по току с помощью нелинейного блока типа «зона нечувствительности» или умножением сигнала задания напряжения на сигнал равный «1» при допустимых токах и на сигнал равный «0» при превышении допустимого тока. Параметры реле на рис. 10: [10 10 10 0].

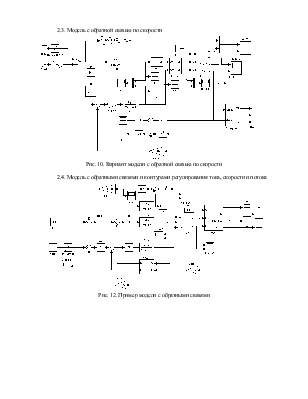
2.3. Модель с обратной связью по скорости

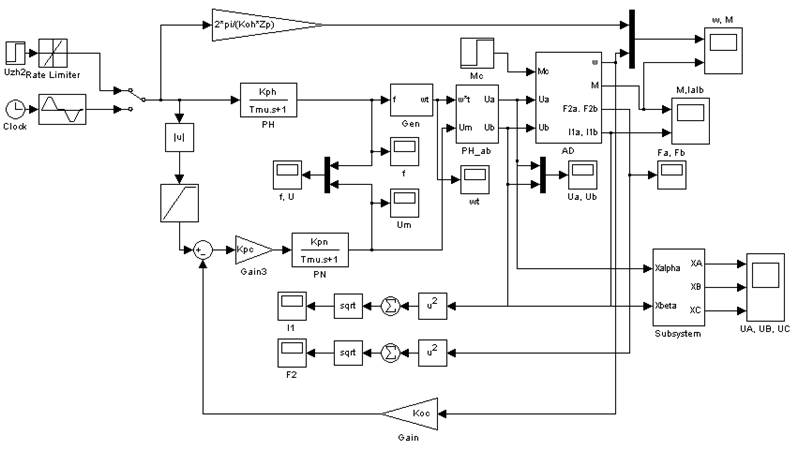
Рис. 10. Вариант модели с обратной связью по скорости

2.4. Модель с обратными связями и контурами регулирования тока, скорости и потока

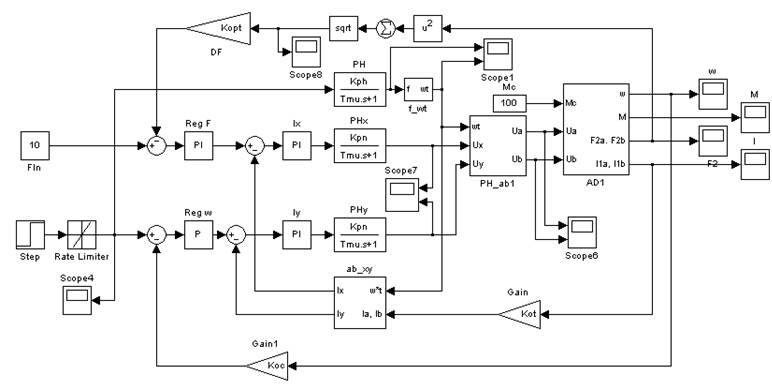
Рис. 12. Пример модели с обратными связями

3. Расчет параметров моделей

Параметры моделей в пп. 2.1-2.3:

L12=0.19003          %максимальная взаимная индуктивность между любой обмоткой

%статора и любой обмоткой ротора при совпадении их осей

L1=0.19335          %полная эквивалентная индуктивность обмотки статора (L1=L1s+L12)

L2=0.19667           %полная эквивалентная индуктивность обмотки ротора (L2=L2s+L12)

R1=2.3295

R2=1.4676

Zp=3

Jdv=0.18

K2=L12/L2           %коэффициент электромагнитной связи ротора

T1=(L1-(L12^2)/L2)/(R1+(K2^2)*R2)

T2=L2/R2

Jmeh=1

J=Jdv+Jmeh

Unom=310

fnom=50

Mnom=38.4

Tmu=0.002

Kph=5

Koh=1/5

Imax=51

Trh=2*Tmu*Koh*Kph

Kpn=32

Kon=1/32

Trn=2*Tmu*Kon*Kpn

Параметры модели в п. 2.4:

L12=0.004          %максимальная взаимная индуктивность между любой обмоткой

%статора и любой обмоткой ротора при совпадении их осей

L1=0.00412          %полная эквивалентная индуктивность обмотки статора (L1=L1s+L12)

L2=0.00424           %полная эквивалентная индуктивность обмотки ротора (L2=L2s+L12)

R1=0.0093

R2=0.0062

Zp=3

Fnom=0.86

Jdv=10

K2=L12/L2           %коэффициент электромагнитной связи ротора

T1=(L1-(L12^2)/L2)/(R1+(K2^2)*R2)

T2=L2/R2

Usau=10

Uogr=100

Tmu=0.002

Jmeh=0

J=Jdv+Jmeh

Unom=310

fnom=50

Mnom=1500

wn=100

Imax=1000

Kph=5

Kpn=31

Kot=Usau/Imax

Koc=Usau/wn

Kopt=Usau/Fnom