Расчет линейных электрических цепей переменного тока. Расчет разветвленных цепей синусоидального тока комплексным методом

частоте  f  комплексное сопротивление нагрузки Z = 5100 + j3000 Ом. Найти мгновенное значение тока в нагрузке.

Решение

Определяем направления токов ветвей и напряжений U^&₁ и U^&₂  узлов 1 и 2 как на рис. 3.8. Принимаем E& = Е.

Уравнения метода узловых напряжений имеют вид

 1 + 1 + 1 U&1 − R12 + Z1C U&2 = I&

 R1     R2       Z C       



= RE&₁ ;Z

откудаU&₂ = µ U&₁,                                                                 _Рис. 3.8         

              U& 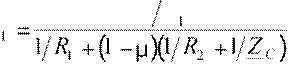E& R _.

Комплексное сопротивление емкости  С на частоте ω = 2π f = 6283 c^-1 Z _C = − jωC = −3,18⋅10³ j Ом. 

Тогда 

        U&₁ = _^1600                                 ^^ =0,83e j155o В;

                                                                   ^ 2700 − j3,18⋅₁₀^{3 }_

             U&₂ = µU&₁ = e− j180^o 0,83e j155^o = 0 83, e− j25o В.

Комплексное действующее значение тока нагрузки I& ^{= U&2} = −8 026 10, ⋅ ⁻⁵ +1154 10, ⋅ ⁻⁴ = 1405 10, ⋅ ⁻⁴ e ^j125o А. Z

Мгновенное значение тока  определяется по выражению:

i = Im( 2Ie& ^{j tω} ) = Im( 2 ⋅1,405⋅10⁻⁴ e ^j125oe ^jωt ) = 2⋅10⁻⁴ sin(ωt +125^o) А.

Задача 3. 8

В цепи со схемой замещения рис. 3.9 действующее значение синусоидальной э. д. с.  Е = 2 В. Частота f = 1000 Гц;

R₁ =160 Ом; R₂ =2700 Ом; I&

R₃=30000 Ом; C = 0,1 мкФ,

G = 0,001 Ом^–1. На частоте f Z комплексное сопротивление нагрузки 

                Z = 300 + j600 Ом.                                           _Рис. 3.9

Найти мгновенное значение тока в нагрузке. Рассчитать баланс мощностей.

Решение

Назначаем направления токов и напряжений U^&₁₀ ; U^&₂₀ узлов как на рис. 3.9. Уравнения первого закона Кирхгофа для узлов 1 и 2 имеют вид:

− I&₁ + I&₂ + I&₃ + I&_C = 0; I& − I&₄ − I&₃ − I&_C = 0.

Выражаем токи ветвей через напряжения U^&₁₀ и U^&₂₀ :

I&1 = E& −RU1&10 ; I&2 = UR&102 ; I&3 = U&10 R−3U&20 ; I&C = U&10Z−CU&20 ; I& = U&Z20 ;

I&₄ = GU&₁ = G(E& −U&₁₀),  получаем узловые уравнения:

 1 + R1 + 1 + 1 U&10 −  R1₃ + Z1_C U&20 = RE&₁ ; 

                R_{1          2}        R₃       Z _C         

−  R¹₃ + Z¹_C − G^U&₁₀ + ^ Z¹ + R¹₃ + Z¹_C ^U&₂₀ = GE&.

В узловых уравнениях для схем цепей с зависимыми источниками в общем случае Y12 ≠ Y 21.

Ток нагрузки равен

I& ₌ U&20 .

Z

Комплексные мощности источника Sист и нагрузок Sпот  соответственно равны:

Sист = E E& −U&10 ; 

R₁

Sпот =UR112 + UR1022 + UR1232 + UZ12C2 + UZ20 −U&20I4,

где E и I₄– сопряженные комплексные значения э. д. с. E& и тока I^&₄, U₁; U₁₀ ; U₁₂ ; U₂₀ – действующие значения напряжений. 

Внимание. При расчете по этим выражением комплексных мощностей знак + перед реактивной мощностью в выражении S = P + jQ соответствует емкостному характеру нагрузки.

Численное решение в пакете Mathcad приводится ниже.

R1 160.0  R2  2700  R3 30000  z     300         j .600 ← Исходные ^данные

C0.1 10.           6  G0.001  f1000  E          2           ← Расчет комплексного сопро-

тивления емкости на частоте f

ω2.π.f  ω = 6.283103                zc      ωj.C                            ← комплексных Расчет собственныхпроводимостей и общих  

Y11    R11¹ R2¹1  R31 zC1     Y22Y21 1z¹ R31 ¹ zC1G                 ← Расчет матрицы  узловых

Y12

R3Y11zC                          Y12               R3     zC                         проводимостей  

 Ynn        Y21   Y22                                                                    

J11     R1^E   J22    G.E    Jnn   ^J11J22                 _← ←  РасчетРасчет  узловыхузловых  токовнапряжений     

Un0     Ynn ¹.Jnn    Un0 =    1.738      0.215j                                

0.605 + 1.247j

u10        Un0₀   u20Un0₁   u20 = 0.605 + 1.247j                        

i      ^u20z i = 1.259 10 ³ + 1.63810 ³ j                                  ^←вующего Расчет значения комплекса тока  нагруздейст_-Im 2. i    Im = 2.922^{10 3} ки←  Расчет амплитудного значеψ_i 180.arg(i)    ψ_{i = 52.457} ния тока нагрузки

π     ← Расчет начальной фазы тока  нагрузки

U1       E     u10   U10        u10    U12       u10    u20 ← Расчет действующих значе-

U20     u20      ний напряжений для баланса      мощностей 2 2             2             2               2

Sz                                                                                                 u20 G (. . E u10) ← Комплексная мощность нагрузок

Se                                                                                 ← Комплексная мощность ис-

точника  Sист

Из расчета следует:

− амплитудное значение тока нагрузки I_m = 2,92 мА;

− начальная фаза ^ψ_i =52,5^°, следовательно, мгновенное значение тока i(t) = 2,92sin(ω t + 52,5^o) мА. Комплексные мощности:

− Sист = 3,28⋅10⁻³ + 2,687⋅10⁻³ j ВА; − Sпот = 3,28⋅10⁻³ + 2,687⋅10⁻³ j ВА.

Баланс выполняется,  Sист = Sпот .

Задача 3. 9

В цепи с операционным усилителем ОУ (схема на рис. 3.10) действующее значение синусоидальной э. д. с. Е =1 В. Частота  f = 1000 Гц. Найти амплитудное значение напряжения U&_выхи угол сдвига фаз ψмежду этим напряжением и э. д. с. E& .  Параметры элементов ветвей: R₁ =2300 Ом; R₂ =R₁; R = 5100 Ом; С₁ =0,068 мкФ; С₂ =С₁. Операционный усилитель – идеальный. 

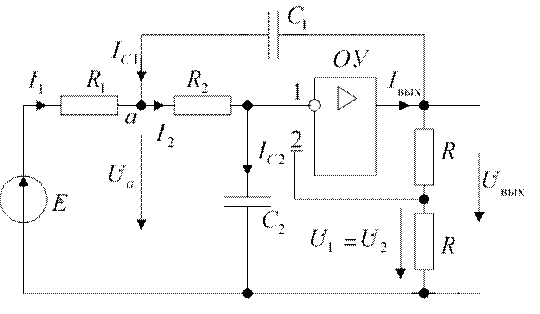
Рис. 3. 10

Решение

Назначаем положительные направления токов ветвей как на  рис. 3.10. Пусть E& = E= 1 В.

Идеальный  ОУ  не потребляет ток по входам 1 и 2, поэтому I^&₂ = I^&_C2 Напряжение U&₁ = U&₂ = U&_вых 2.

Уравнения первого закона Кирхгофа для узлов  а и 1  имеют вид: − I&₁ + I&₂ − I&_C1 = 0 − I&₂ + I&_C2 = 0.

Выражаем токи ветвей через напряжения U^&_a и U&_вых:

I&1 = E& −R1U&a ; I&2 = U&a −RU&2вых 2 ; I&C1 = U&выхZ C−1U&a ; I&C2 = 2U&ZвыхC2 .

Получаем узловые уравнения:

                1 + 1 + 1 U&a − 21R2 + Z1C1 U&вых = RE&1 ;

               R1      R2       Z C1        

 − R1 U&a +  21R2 + 2Z1C2 U&вых = 0.

2

Следует обратить внимание, что в узловых уравнениях  Y₁₂ ≠ Y ₂₁.

Численное решение в пакете Mathcad приводится ниже.

R1     2300   R2     R1   R  5100  C1  0.068 10.        ⁶    ←  Исходные данные.

C2      C1    E     1

rg                                                                     ← Формула перевода из ради¹    zc2 j ._ω¹0.C2 противлений←ан  в Расчетградусы комплексных.  емкостей на  чассо-тоте f.

← Расчет узловых напряжений  U^&_a и U&_вых .

← Расчет U&_вых .

← Расчет начальной фазы выходного напряжения. ← Расчет амплитудного значения выходного напряжения. Комплексное действующее значение

U&_вых = 0,07 − 2,03 j = 2,033e^{− j88o} В.

Амплитудное значение U_m = 2 2,033⋅ = 2,88 В. 

Поскольку E& = 1e ^j0o , то угол сдвига фаз ψ = 0− ( 88 )− ^o = 88^o.

Примечания. Для цепи со схемой рис. 3.10 узловые уравнения можно записать непосредственно по виду схемы:

                1 + 1 + 1 U&a − R12 U&1 − Z1C1 U&вых = RE&1 ;

                R1      R2       Z C1 



− R1₂ U&a + R12 + Z1C2 U&1 = 0;

U&₁ −U&^вых2 = 0, откуда

 1 + 1 + 1 U&a − 21R2 + Z1C1 U&вых = RE&1 ;

         R1    R2      Z C1       



− R1 U&a +  21R2 + 2Z1C2 U&вых = 0.

                         2               

Задача 3.10

Для электрической цепи со схемой рис. 3. 11 найти комплексное действующее значение тока I&.

                                           ^Z         I& ПараметраY _{1 =}0, 02  j  _Омэлементов –1; Z _{2 =} 80ветвей j _Ом; :

Z ₃ = 60 Ом; Z =50 Ом; ³ E& =– 100 В; J& =0,1 j А.

                                                                                                  E^&    Решение

Для расчета тока одной ветви удоб но избрать метод эквивалентного

                                           Рис. 3.11                               генератора.

Определяем э. д. с. эквивалентного генератора. Разрываем ветвь с сопротивлением Z . Рассчитываем напряжение холостого хода U^&₀ (рис. 1.12).

                                      U^&₀      Уравнениедля контура второго, указанного закона на Кирхгофа рис. 3.12,  

Находим:

I&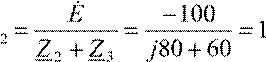e ^j127o А;I&₁ = J& = j 0,1 А;

^o ⋅80 j = 69 + 48 j = 84 e ^j35o В.

Определение  комплексного сопротивления эквивалентного генератора  ZГ поясняет схема рис. 3.13.

                                                                                 Z 3                            ZГ = Y¹ + ZZ 2+ZZ3 3 =

                                                                                                                                        1            2

                                                                                             = 38,4– 21,2 j = 43,86 e^{− j29o} Ом.

                                      Рис. 3.13                                       

Ток I& определяем из уравнения

I& = ZГU&+0 Z = 43,8684e−ejj2935oo + 50 =0,615+0,69j = 0,82e j47,5o А.

Рассчитаем ток I& методом наложения.

В соответствие с методом ток ветви линейной электрической цепи определяется как алгебраическая сумма частичных токов, вызываемых действием каждого источника в отдельности.

Рассчитаем ток  I^&₀₁ от действия источ- Z I&₀₁ ника тока J& (схема рис. 3.14).

Комплексное сопротивление Z 023 = Z + ZZ 2+ZZ3 3 = 

2

= 50 + 38,4 + 28,8j = 88,4 + 28,8j =

Комплексная проводимость                                                Рис. 3.14

Y  = Y _{1 +} ¹ =0, 02 j + 0.0102 – 3.33 ⋅10 ^–3 j  = 0,0102 + 0,017 j =  Z 023

= 0,0196 e ^j58o Ом ^–1.

Ток

I&01 = YZJ&023 = 0,0196e0,j158jo 93e j18o = 0,0535+0,013j А.

Рассчитаем ток  I^&₀₂ от действия источ- Z I^&₀₂ ника тока  J& (схема