Промышленность \ Производственные технологии

Анализ термодинамических процессов и циклов в тепловых двигателях и установках. Определение начальных параметров газа, страница 3

, где: удельная средняя массовая изобарная теплоёмкость, ,

6 Количество теплоты , Дж/ч, отводимое от газа в одной ступени вычисляется по выражению.

, где: - удельная средняя массовая теплоёмкость политропного процесса, ; определяющаяся по выражению

, где: - удельная средняя массовая изохорная теплоёмкость, ,

(воздух)

, следовательно

7 Общее количество теплоты , Дж/ч, отводимое от газа в компрессорной машине

, где: - число промежуточных холодильников

8 Количество охл. воды , прокачиваемой через компрессорную машину, кг/ч,

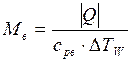, где: - удельная средняя массовая изобарная теплоемкость воды, , принимаем .

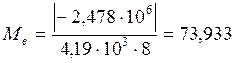
9 Изменение энтропии в процессе политропного сжатия в ступени компрессора, ,

10 Расчетные точки, для построения графика процесса политропного сжатия в координатах

, К	, кДж/К
300	0
315	-0,137
330	-0,267
345	-0,391
360	-0,511
377,75	-0,645

11 Работа , Дж/ч, эквивалентного одноступенчатого компрессора

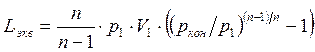
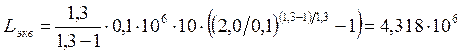
12 Теоретическая мощность , Вт, эквивалентного одноступенчатого компрессора

13 Производительность , м³, эквивалентного компрессора из уравнения

, отсюда выразим

14 Расчетные точки, для построения графика процесса эквивалентного одноступенчатого компрессора в координатах

, МПа	, м³
0,10	10,00
0,40	3,443
0,80	2,020
1,20	1,479
1,60	1,185
2,00	0,998

15 Температура , К, в конце политропного сжатия определится из

, отсюда

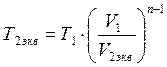
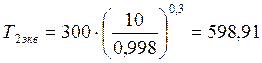
16 Изменение энтропии в многоступенчатом компрессоре,

17 Расчетные точки, для построения графика процесса изобарного охлаждения в многоступенчатом компрессоре в координатах

, К	, кДж/К
377,75	0
360	-0,565
345	-1,064
330	-1,586
315	-2,132
300	-2,705

18 Полное изменение энтропии , , в политропном процессе сжатия в эквивалентном одноступенчатом компрессоре

19 Расчетные точки, для построения графика процесса политропного сжатия в координатах

, К	, кДж/К
300	0
360	-0,511
420	-0,942
480	-1,316
540	-1,646
598,91	-1,936

Задача 3. Для идеального цикла ДВС определить параметры , и во всех характерных точках, количество подведённой и отведённой теплоты, работу цикла, изменение энтропии и термический КПД, если известны начальные параметры , , и безразмерные характеристики , , . Рабочее тело - воздух, процессы сжатия и расширения - политропные с показателями соответственно и (согласно таблице 3), удельные теплоёмкости - независимые от температуры. Для определения термического КПД вывести расчётную формулу. Построить цикл ДВС в и диаграммах в масштабе.