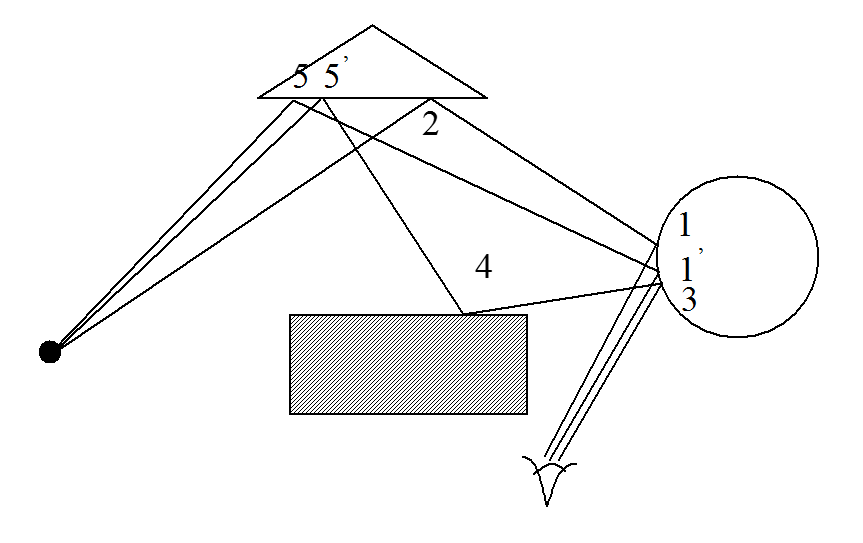
Модель глобального освещения с трассировкой лучей. Сфера, призма, параллелепипед. Алгоритм трассировки лучей

Модель глобального освещения с трассировкой лучей

• В случае глобальной модели учитывается свет, отраженный от поверхности объекта, а также свет, отраженный от других объектов сцены или пропущенный сквозь эти объекты.

Сфера, призма, параллелепипед - непрозрачные, но поверхности их зеркальные. В точке 1 наблюдатель видит не только сферу, но и точку 2 на призме. Хотя призма закрыта от наблюдателя параллелепипедом, тем не менее, она становится видимой из-за отражения ее на сфере.

Точка 5 (5') призмы видна в результате отражения от обратной стороны параллелепипеда в точке 4 к точке 3 на сфере и затем - к наблюдателю. Кроме того, наблюдатель видит точку 5 в точке 1' на сфере после одного отражения на сфере. Таким образом, на сфере находятся 2 изображения призмы. Изображение, расположенное вокруг точки 1, повернуто, так как получается после одного отражения; вокруг точки 3 не повернуто, так как получается после двух отражений. Интенсивность отраженного света в точке 3 меньше.

Кроме того, в сфере отражается обратная сторона параллелепипеда, то есть наблюдатель видит ее, хотя на нее не падает прямой свет источника. Эта сторона освещается рассеянным светом и светом, отраженным от других объектов сцены.   Таки образом, в глобальной модели нельзя отбрасывать задние (невидимые непосредственно) грани объектов. Решение задачи построения глобальной модели освещения требует использования алгоритмов выделения видимых поверхностей, с помощью алгоритмов трассировки лучей.

Алгоритм трассировки лучей

Если отслеживать свет, испускаемый источником, то вычислительный процесс будет малоэффективен, так как только небольшая часть света, испущенного источником, доходит до наблюдателя. Поэтому было предложено отслеживать (трассировать) лучи в обратном направлении от наблюдателя к объекту.   На этой основе были реализованы алгоритмы трассировки лучей с использованием общих моделей освещенности. Эти алгоритмы учитывают эффект отражения изображения одного объекта от поверхности другого, преломления, прозрачности и затенения. В этих алгоритмах предполагается, что сцена преобразована в пространство изображений.

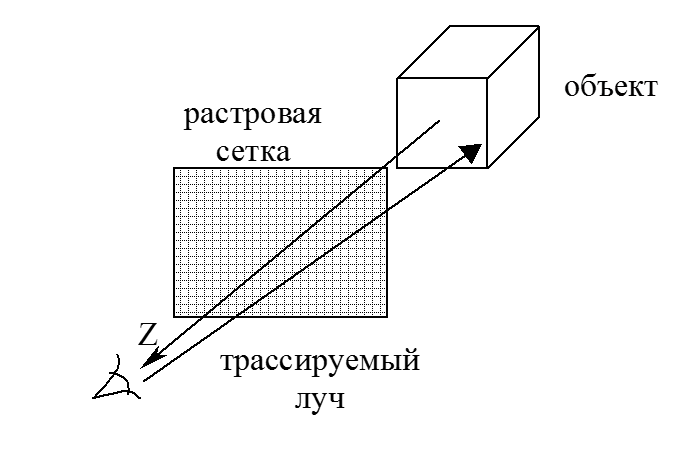
Пусть наблюдатель находится в бесконечности на положительной полуоси z. Каждый луч, исходящий от наблюдателя, проходит через центр пикселя до сцены. Траектория каждого луча отслеживается, чтобы определить, какие объекты сцены пересекаются с данным лучом. Необходимо проверить пересечение каждого объекта сцены с каждым лучом. Если луч пересекает объект, то проверяются все возможные точки пересечения. Можно получить множество пересечений. Эти пересечения упорядочиваются по глубине. Пересечения с максимальным значением z представляют видимую поверхность для данного пикселя. Атрибуты этого объекта используются для определения характеристик пикселя.

Если точка зрения находится не в бесконечности, то алгоритм незначительно усложняется. Наблюдатель по-прежнему находится на положительной полуоси Z. Растр перпендикулярен оси Z и строится одноточечная центральная проекция на растровую сетку.   Нужно учесть, что до 95% времени при реализации алгоритма трассировки лучей уходит на определение пересечений, при этом в состав сцены могут входить любые объекты, для которых можно найти процедуры построения пересечений.

Для сокращения времени поиска пересечений можно рассматривать пересечения луча с объемной оболочкой рассматриваемого объекта. Если луч не пересекает оболочки, то не нужно больше искать пересечений этого объекта с лучом. В качестве оболочки выбирают сферу, параллелепипед и другие объекты простой формы. Проще определить факт пересечения луча в трехмерном пространстве со сферой. Надо найти расстояние от центра сферы до луча и, если оно больше радиуса сферы, то луч не имеет пересечения и с объектом. (Правда, эффективность использования сферы в качестве оболочки может оказаться небольшой).

Формулы для расчетов достаточно просты.   Пусть прямая, проходящая через точки P1(x1, y1, z1) и P2(x2, y2, z2), задана параметрически. P(t) = P1 + (P2 - P1)t, то есть x(t) = x1 + (x2 - x1)t = x1 + at y(t) = y1 + (y2 - y1)t = y1 + bt z(t) = z1 + (z2 - z1)t = z1 + ct

Минимальное расстояние d от этой прямой до точки P0(x0, y0, z0) равно: d2 = (x - x0)2 + (y - y0)2 +(z - z0)2, где параметр t, определяющий ближайшую точку P(t), t = [a(x1 - x0) + b(y1 - y0) + c(z1 - z0)]/( a2 + b2+ c2) Если d2 > R2 (где R - радиус сферической оболочки), то луч не может пересечься с оболочкой.