Реалистические изображения. Принципы создания, модели, алгоритмы. Учет физических и психологических факторов

Реалистические изображения

Принципы создания, модели, алгоритмы

Учет физических и психологических факторов

2 типа рецепторов: палочки и колбочки. Палочки – чувствительны к низким уровням освещенности. Колбочки – различаю цвета и мелкие детали. Предел чувствительности к яркости  1010 Чувствительность к относительной яркости - ~ 100 – 150 (2.2 логарифмической единицы)

Простая модель освещения

Диффузное отражение света

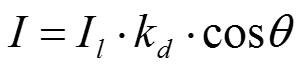
I – интенсивность отраженного света Il – интенсивность точечного источника kd – коэффициент диффузного отражения 0  kd  1  - угол между направлением света и нормалью к поверхности 0    /2

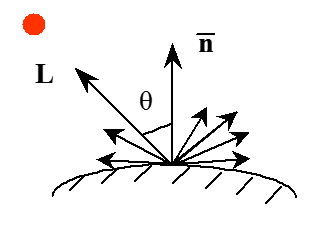
0    /2 Ia- интенсивность рассеянного света ka- коэффициент диффузного отражения рассеянного света 0  ka  1

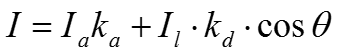
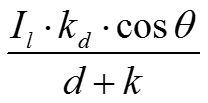
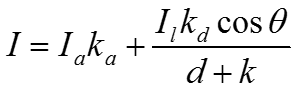
d - расстояния от источника до объекта k – произвольная постоянная

Зеркальное отражение света

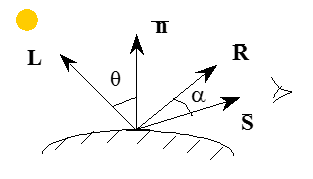
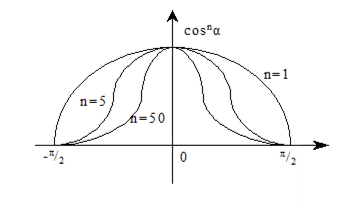
Эмпирическая модель Фонга.

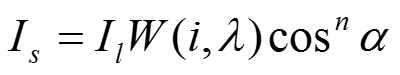
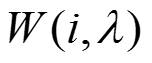
- кривая отражения представляющая отношение зеркально отраженного света к падающему, как функцию угла падения i и длины волны - .

n – степень, аппроксимирующая пространственное распределение зеркально отраженного света

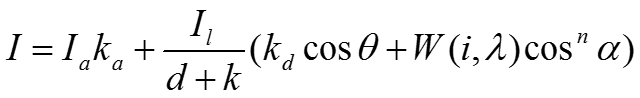
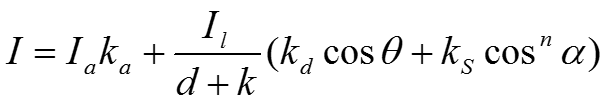
- функция закраски

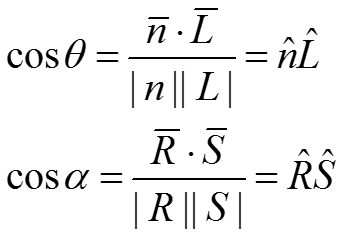
- нормаль к поверхности

- направление на источник

- вектор, определяющий направление отраженного луча

• вектор, определяющий направление наблюдения
• (все векторы единичные)

Тогда модель освещенности для одного источника

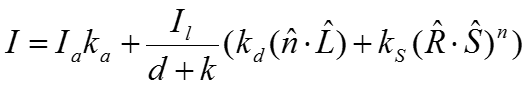
В случае нескольких (m) источников света:

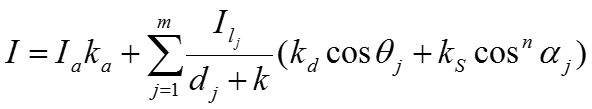
Пример простой модели освещения

Вектор нормали

Вектор падающего света

Вектор наблюдения

Вектор отражения = ?

Анализируем вектор падающего света …

Вектор отражения =

Пусть на сцене находится один объект, d=0, k=1. Интенсивность источника в 10 раз больше, чем рассеянного света, т.е.

Поверхность объекта блестящая металлическая, свет, в основном, отражается зеркально, т.е.

.

.

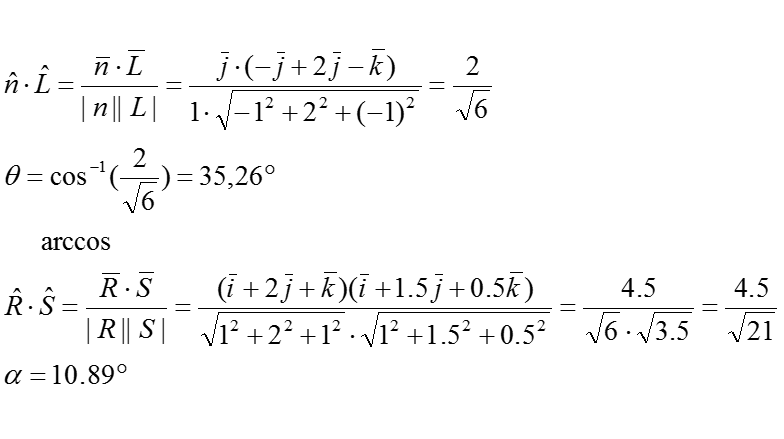
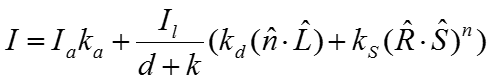
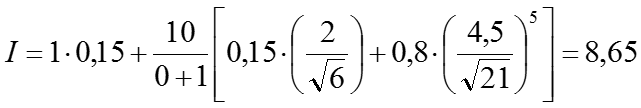
При изменении положения наблюдателя

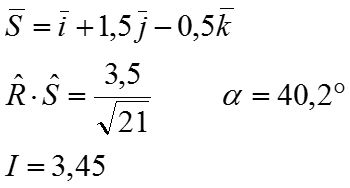
Нахождение нормали к поверхности

• Варианты задания поверхности:
• при аналитическом задании поверхности нормаль вычисляется непосредственно
• во многих задачах поверхность представляется полигональной аппроксимацией, тогда зная уравнение плоскости каждого полигона, можно найти уравнение внешней нормали
• во многих алгоритмах удаления невидимых линий и поверхностей используются только ребра или вершины, тогда находится приближенное значение нормали на ребрах или вершинах

Пусть заданы уравнения плоскостей полигональных граней, тогда нормаль к их общей вершине равна среднему значению нормали по всем многоугольникам, сходящимся в этой вершине.

Возьмем усеченную пирамиду:

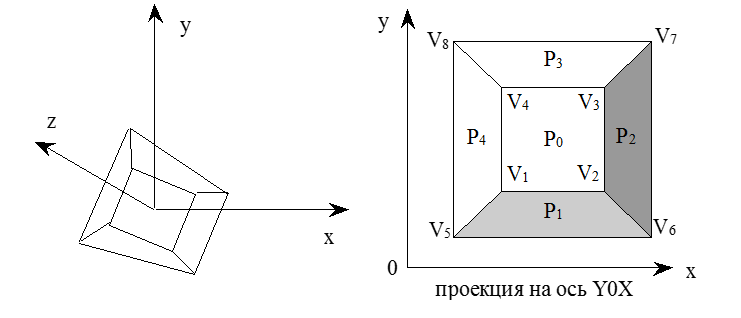
В точке V1 направление приближенной нормали будет определяться уравнениями плоскостей многоугольников , окружающих V1.

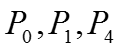
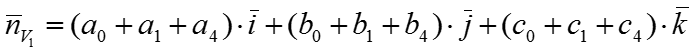
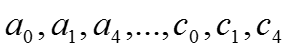
где

- коэффициенты уравнения плоскостей многоугольников

Если уравнения плоскостей не заданы, то нормаль к вершине можно определить, усредняя векторное произведение всех ребер пересекающихся в вершине. Тогда:

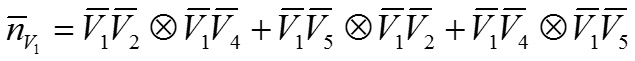
Величина вектора зависит от количества и площади конкретных многоугольников, а также количества и длины конкретных ребер.

Пример.

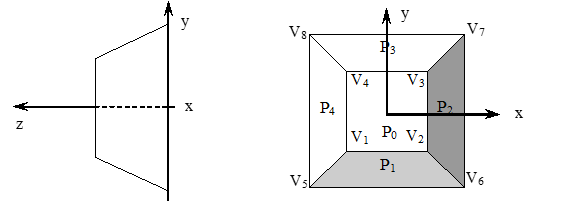
Координаты вершин:

V1 (-1; -1; 1) V2 ( 1; -1; 1) V3 ( 1; 1; 1) V4 (-1; 1; 1) V5 (-2; -2; 0 V6 ( 2; -2; 0) V7 ( 2; 2; 0 V8 (-2; 2; 0)

Запишем уравнения плоскостей для граней P0, P1, P4:

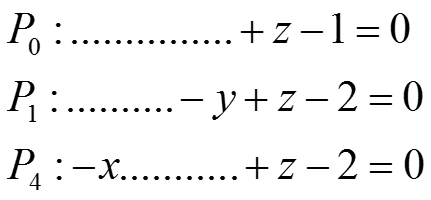
Найдем приближенную нормаль в точке V1, усредняя нормали к окружающим многоугольникам

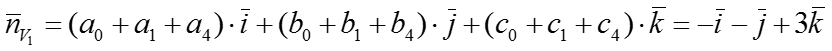
Абсолютная величина нормали может быть записана как

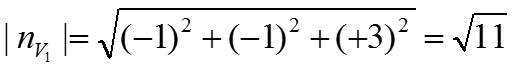
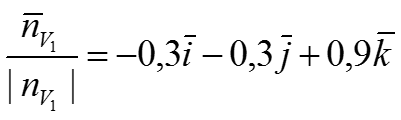
Единичная нормаль

Другой способ: Найдем выражение нормали через векторное произведение ребер, сходящихся в вершине V1.

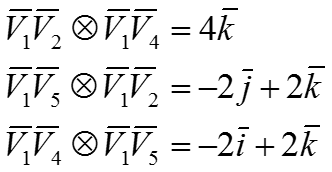
В этом случае, усредняя векторное произведение, получим нормаль в точке V1:

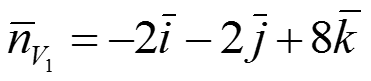
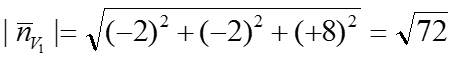
Абсолютная ее величина:

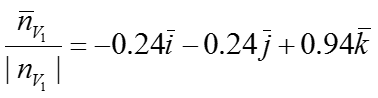
Единичная нормаль:

Т.е. нормали, полученные двумя способами, различны как по величине, так и по направлению, освещение будет отличаться,

результат будет различным.

Определение вектора отражения.

Если свет падает вдоль оси z:

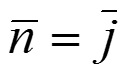
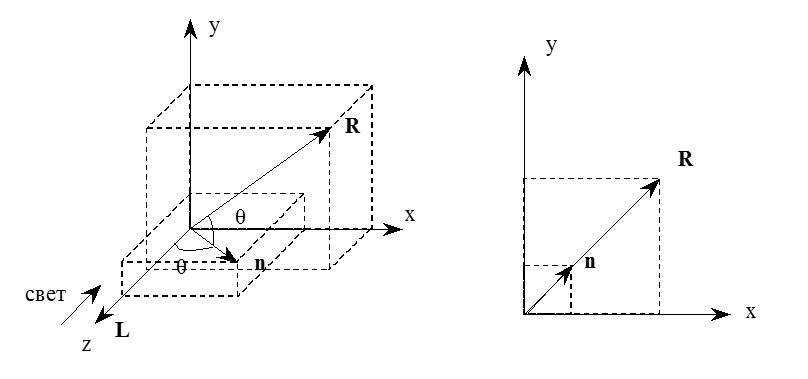
Тогда, - единичная составляющая вектора отражения по оси Х, - единичная составляющая вектора отражения по оси Y, - единичная составляющая вектора нормали по оси Х, - единичная составляющая вектора нормали по оси Y.

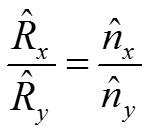
- угол между единичной нормалью и осью Z, то составляющая нормали по оси Z:

Угол между единичным вектором отражения и осью

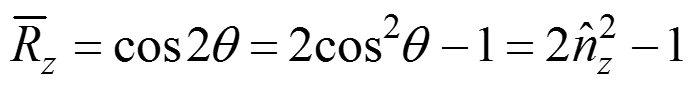
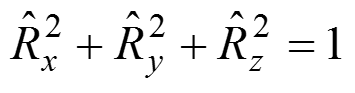
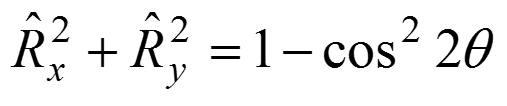
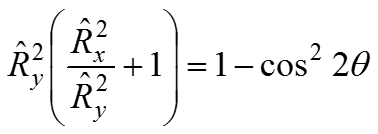
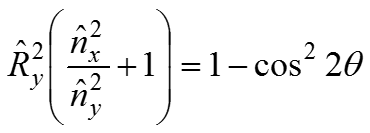
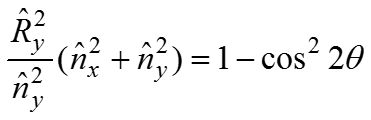
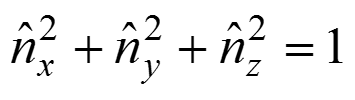
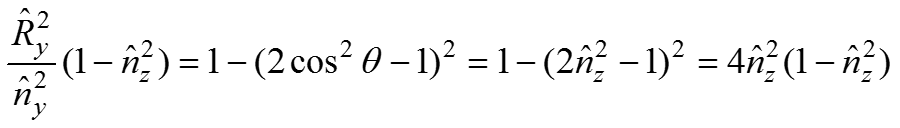
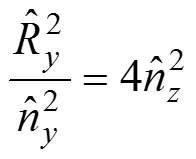
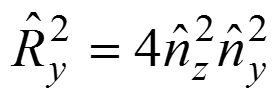
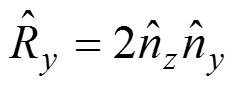
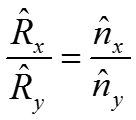
Так как

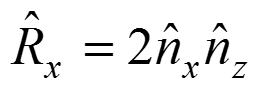
Мы получили составляющие векторы отражения по оси Y через составляющие нормали по оси Y и Z.

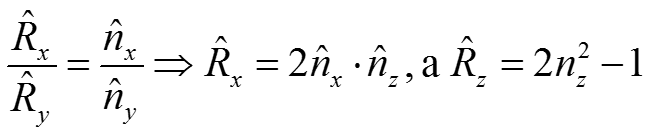
Если свет падает от нескольких источников ………..

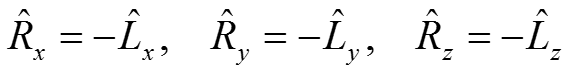
Методы закраски

Закраска методом Гуро.

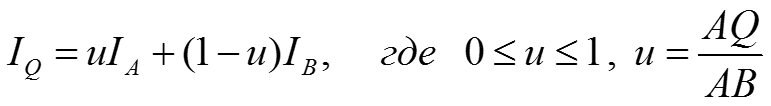
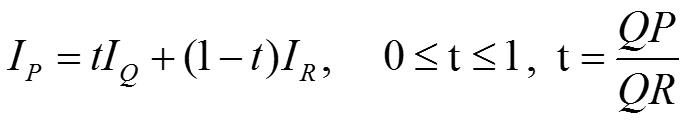
Закраска методом Фонга.

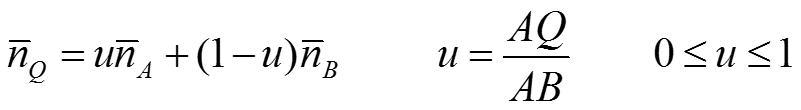
Прозрачность

Преломление рассчитывается по закону Снеллиуса: падающие и преломленные лучи лежат в одной плоскости, а углы падения и преломления связаны формулой:

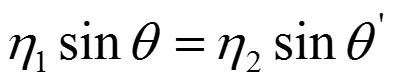
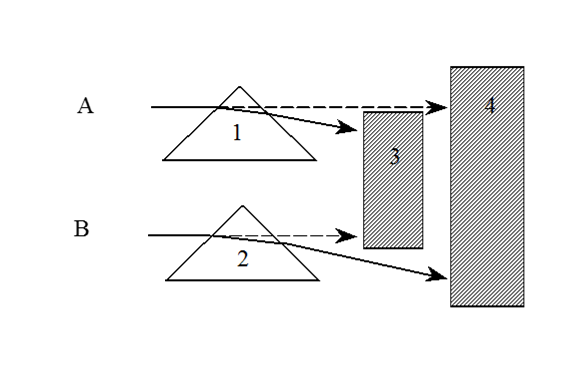
Тени

Тень состоит из 2-х частей: тень и полутень. Тень – центральная резко очерченная темная часть. Полутень – окружающая ее более светлая часть.

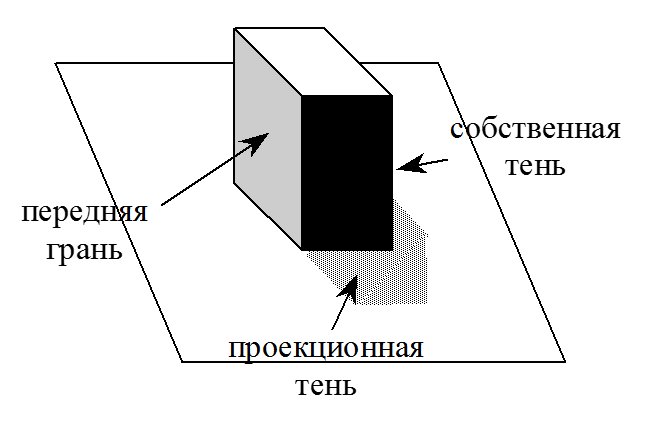
Фактура

ФФактурой называется детализация строения поверхности. ООбычно рассматривается 2 вида детализации: --  на гладкую поверхность наносится заранее заданный узор. При этом поверхность все равно будет казаться гладкой. Наложение узора на гладкую поверхность производится функцией отображения. - 

- на поверхности создаются неровности, шероховатости. Они реализуются путем внесения возмущений в параметры, задающие поверхность.

Задача сводится к преобразованию системы координат.

Если рисунок задан в фактурном пространстве в прямоугольной системе координат ,

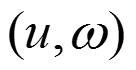
а поверхность в другой прямоугольной системе координат

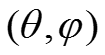
то для нанесения рисунка на поверхность надо найти или задать функцию отображения одного пространства на другое.

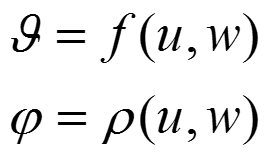
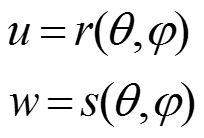
или

Обычно функция отображения линейна:

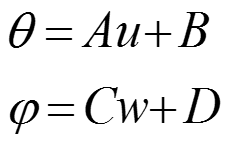
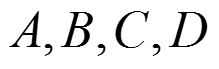
где коэффициенты выводятся из соотношения между двумя известными точками в системе координат.

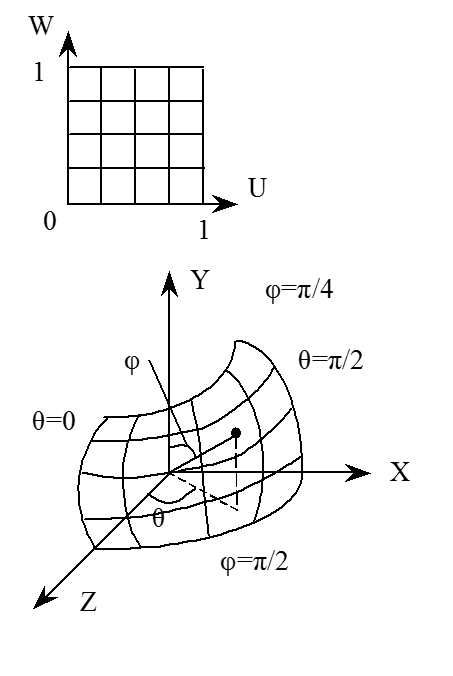
Задача: нанести эту сетку на кусок поверхности, заданный октантом