Другие предметы \ Прикладная механика

Теория механизмов. Планетарные зубчатые механизмы. Ступень с внешним зацеплением. Передаточное отношение всего механизма, страница 3

Передаточное отношение базисного

10

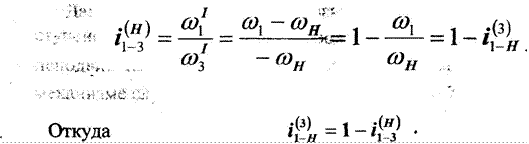
Здесь - передаточное отношение от колеса I к водилу Н при неподвижном колесе З;

- передаточное отношение от колеса 1 к колесу З при остановленном водиле Н (т.е. базисного механизма). Заметим, что верхний индекс в скобках указывает, какое из звеньев остановлено.

Передаточное отношение 4”) базисного механизма может быть вычислено через передаточные числа 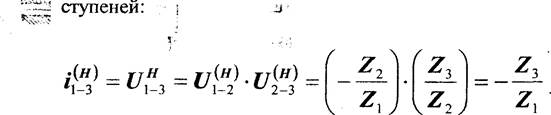ступеней:

Обобщая результат на К— валов, получаем общие формулы для расчета планетарных редукторов:

где п - число внешних зацеплений.

При расчете i(H ) обязательно учитывать знаки. Ошибка в знаке может привести к неправильному результату,

Пример исследования сложного зубчатого механизма

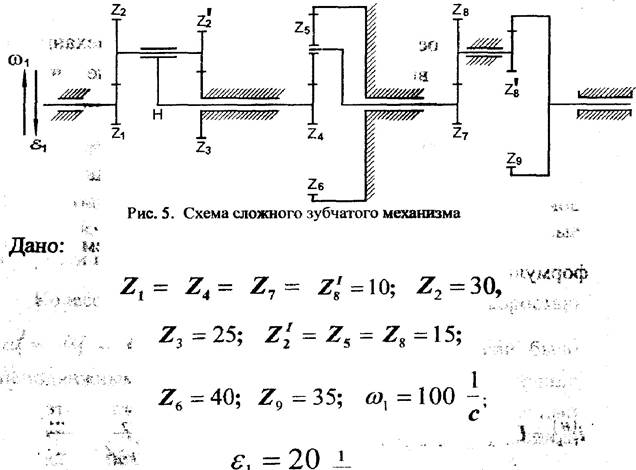
Последовательность анализа сложных зубчатых механизмов удобнее всего проследить на конкретном примере. На рис. 5 изображен зубчатый механизм, для которого необходимо определить все параметры, указанные в условии контрольной работы.

Данный механизм состоит из двух планетарных ступеней (4 — 4) и (Z4 — 4), а также простой ступени с неподвижными осями (4 4). Водилом в первом механизме служит звено 4, а во втором — звено 7.

1.  Передаточное отношение между входным и выходным звеньями равно произведению передаточных отношений составляющих механизмов:

_ Аз)

передаточное отношение первого планетарного редуктора: il_4 1 i(4) =l-Uf 4-4 30-25

4 .73!

Здесь число внешних зацеплений равно двум.

Передаточное отношение второго планетарного редуктора:

=l-i7) =l-d7) =l-d7) .d

Здесь одно внешнее зацепление.

Передаточное отношение ступенчатого редуктора:

4-4 15-35

- -5,25

4.78 10-10

Здесь одна ступень с внешним зацеплением.

Передаточное отношение всего механизма:

 i(3) i(6)      = -4 • 5 .(-5.25) = 105

Знак ”+” говорит о том, что входное и выходное звенья вращаются в одну сторону.

13

2.  Угловую скорость          и угловое ускорение 89

ВЬжОДНОГО звена определяем, используя понятие передаточного отношения:

1

9

100

- 0,952

             [-9       105

                20

0,191    2

105                   С

1-9

З. Движение входного звена замедлено, т.е. 01 и г, направлены в разные стороны.

Время, в течение которого угловая скорость уменьшится до нуля, определяем, используя известное соотношение между о и при замедленном движении:

011 =01 — 81 • t

где 01 — угловая скорость в момент времени с, 01 угловая скорость в начальный момент времени; t — время, в течение которого фиксируется изменение угловой скорости.Время, в течение которого угловая скорость уменьшится до нуля:

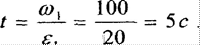
4. Общий коэффициент полезного действия определяется как произведение КПД составляющих механизмов

П =  = 0,45.

14

Контрольная работа

Контрольная работа состоит из одной задачи. Номер варианта схемы механизма выбирается по последней цифре шифра (если эта цифра 0, то выполняется вариант 10), а ЧИСЛОВЫе Данные из соответствующей таблицы по преДпосл@Дней цифре шифра.

Содержание задачи

В зубчатом механизме, показанном на схеме, входное колесо имеет угловую скорость 01 и угловое ускорение , направленное по движению или против движения.

Требуется определить:

1.  Передаточное отношение между входным и выходным звеньями.

2.  Угловую скорость и угловое ускорение выходного звена.

З. Время, в течение которого угловая скорость увеличится в 2 раза (если движение ускоренное) или уменьшится до нуля (если движение замедленное).

4. Общий КПД

В таблице исходных данных 73 - число зубьев колес приводится с индексом, соответствующим его номеру на схеме механизма.

Для расчетов принять следующие значения коэффициентов полезного действия (учитывающие потери и в зацеплении, и в подшипниках): для пары цилиндрических колес = 0,97; для пары конических колес = 0,95; для планетарной передачи с внешними зацеплениями ее колес 0,5; для планетарной передачи, имеющей внутреннее зацепление одной из пар

Скачать файл