Теория механизмов. Планетарные зубчатые механизмы. Ступень с внешним зацеплением. Передаточное отношение всего механизма, страница 2

Требуется найти передаточное отношение it 2 этого редуктора через числа зубьев 4, 732 , Д , 4, а .

1         2               З            4

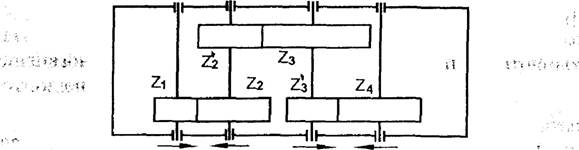
01 02                    03 (04

Рис. 1. Последовательный ряд с кратным зацеплением

Передаточное отношение между валами I и 4 есте отношение их угловых скоростей

4

Знак передаточного отношения пока не фиксируется, т.к. направление 04 по отношению к 01 в принципе не известно.

Вычислим передаточные отношения каждой ступени с учетом знака:

6

1-2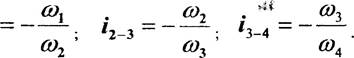

Искомое передаточное отношение l1_4 получим, перемножив эти передаточные отношения:

1-2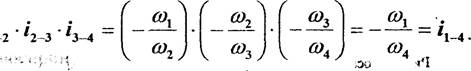

Знак «минус» говорит о том, что валы Ии 4 вращаются в разные стороны.

Используя понятие передаточного числа , получаем:

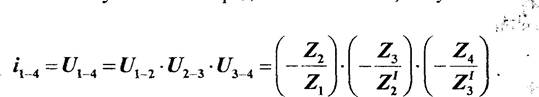
Обобщая результаты на К валов, получим формулу для расчета передаточного отношения многоступенчатого редуктора.

(k-l)-k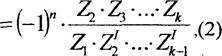

где п - число внешних зацеплений.

Рассмотрим последовательный ряд зубчатых колес (рис. 2), в котором только первое и последнее колеса образуют с соседними по одной зубчатой паре. Промежуточные колеса входят в зацепление одновременно с ДВУМЯ соседними.

1              2                      з                   4

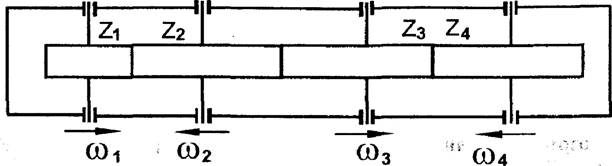
Рис. 2, Последовательный ряд с паразитными Кодрами

При нахождении передаточного отношения этого механизма по выше изложенной методике (формула 2) получаем:

( 4 = Ц 4 = Ul_2 .U2         4

Таким образом, в механизмах подобного типа общее передаточное отношение не зависит от числа зубьев промежуточных (паразитных) колес. Такие схемы применяются, когда необходимо получить нужное направление вращения выходного звена.

Коэффициент  полезного   действия     зубчатых механизмов с неподвижными осями учитывает потери на трение и в зацеплении, и в подшипниках:

 • пап где П - знак произведения; Та - КПД пары подшипников.

8

Планетарные зубчатые механизмы

Планетарными зубчатыми механизмами называются такие механизмы, которые имеют по крайне мере одно звено с подвижной осью относительно стойки.

Водилом Н называется звено, несущее подвижные оси колес (сателлитов). Колеса, оси вращения которых совпадают с осью вращения водила, называются  центральными (солнечными). Центральные колеса и водило являются крайними или основными звеньями. Они воспринимают внешние нагрузки.

На рис. З(а) показан механизм с тремя крайними подвижными звеньями: центральными колесами 7,| и 7-з и водилом н. Этот механизм называется дифференциальным.

 Из дифференциального механизма можно получить планетарный редуктор, если сделать неподвижным одно из центральных колес (7-з на рис. 3(6)).

Как видно из рис. З(а, б), дифференциальный механизм и планетарный редуктор отличаются по структуре от ступенчатого соосного редуктора лишь тем, какие звенья обращены в стойку. Путем закрепления центрального колеса 7,з дифференциал обращается в планетарный редуктор, а при закреплении водила Н — в редуктор с неподвижными осями (рис. 3 в) .

а                                           6                                        В

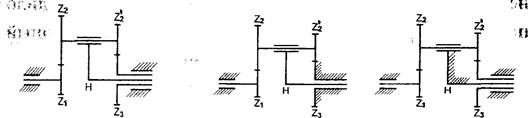
Рис. З. Варианты передач, полученных с помощью остановки различных звеньев; а — дифференциал; б — планетарный редуктор; в редуктор с неподвижными осями

9

Кинематика планетарных механизмов      

Рассмотрим планетарный редуктор Джемса (рис. 4), в котором ведущим является центральное колесо , ведомым — водило Н, а второе центральное колесо Z3 ;неподвижно.

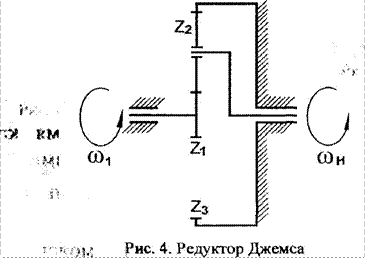
н»

, ' ЭОН

Для нахождения передаточного отношения редуктора „(н)1-3 применим метод обращения движения (инверсии). Мысленно сообщим всем звеньям дополнительное вращение с угловой скоростью - он . В результате угловые скорости всех звеньев изменятся на величину - он .

Колесо Z1 будет вращаться с угловой скоростью

— ^ОТ, колесо 4, которое до инверсии было неподвижным, с угловой скоростью о он . Водило при этом остановится, и механизм обратится в обычный редуктор с неподвижными осями , относительно водила (базисный механизм).