Исследование влияния параметров системы (регулятора) на устойчивость и качество регулирования

Министерство образования и науки Российской Федерации Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

ИССЛЕДОВАНИЕ линюйН0й СИСТЕМЫ

АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ п-РАЗБИЕНИЙ

Методические указания к выполнению лабораторной работы по дисциплине

«Теория автоматического управления» для студентов специальности 220201.65 всех форм обучения

Одобрено  реДакционно-изДательским советом

Балаковского института техники, технологии и управления

Балаково 2010

Цель работы:

1. Исследование влияния параметров системы (регулятора) на устойчивость и качество регулирования.

2. Освоение методики построения кривой Dразбиения в плоскости 2-х параметров.

ОСНОВНЫЕ ПОНЯТИЯ

Устойчтвость системы автоматического регулирования (САР) является необходимьпи условием ее работоспособности. Переходный процесс в линейной системе описывается выражением:

п 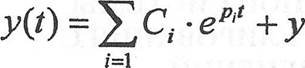уст = Уд (t) +ууст ,       (1)

где уд (О - переходная составляющая;

ууст - вынужденная составляющая;

Pi - корни характеристического уравнения системы; Ci - постоянные интегрирования.

Система называется устойчивой, если ее переходная составляющая стремится со временем к нулю: lim уп (О = О    (2)

Для устойчивости системы необходимо и достаточно, чтобы корни ее характеристического уравнения имели отрицательные вещественные части. Устойчивость системы зависит от коэффициентов ее характеристического уравнения. Коэффициенты характеристического уравнения в свою очередь зависят от параметров системы, например, от коэффициентов Ко и kl регулятора.

Область изменения параметров, при которых система устойчива, называется областью устойчивости системы. Для выделения области устойчивости может использоваться метод Тразбиения.

Пусть дано характеристическое уравнение п-ой степени:

                  А(р) = рп + ап_1рп-1 + +                           (3)

При заданном значении коэффициентов уравнения в общем случае оно имеет т корней в правой полуплоскости и (п-т) корней в левой полуплоскости. При изменении коэффициентов уравнения корни его также изменяются и, следовательно, перемещаются в плоскости корней, описывая определенную кривую. При некотором значении коэффициентов один из действительных корней характеристического уравнения попадает на мнимую ось и становится равным 0, а при выходе на мнимую ось двух комплексных сопряженных корней характеристического уравнения имеет два чисто мнимых корня ± jw. Значения этих коэффициентов удовлетворяют уравнению:

^l+.. .+ao=O      (4) Уравнение (4) в (п-1) мерном пространстве коэффициентов, по осям которого отложены коэффициенты ао, щ, ф, ап соответствует точка при данном значении частоты w. При изменении w от (— оо;+оо) получаем поверхность A(jw)=O. Если перемещаться в пространстве уравнения, т.е. менять коэффициенты уравнения, то при некотором их значении мы пересечем поверхность A(jw)=0 и следовательно пара или один корень будет переходить из правой (левой) полуплоскости корней в левую (правую). рЗ+чр2+щр+ао=0  (5)

Каждому из коэффициентов ао, щ, ф, ап в трехмерном пространстве соответствует точка. Этому значению коэффициентов уравнения соответствует определенное расположение корней в плоскости корней.

При некоторых значениях коэффициентов некоторые корни окажутся на мнимой оси, т.е. корни будут иметь вид (0± jWl ), следовательно, соответствующая точка в пространстве будет удовлетворять уравнению:

                               (6)

Рисунок 1. Расположение корней характеристического уравнения

Уравнению (6) при изменении частоты от — до 00 соответствует поверхность S в пространстве коэффициентов. При изменении коэффициентов характеристического уравнения его корни изменяются и попадают на мнимую ось только тогда, когда точка в пространстве коэффициентов попадает на поверхность S.

 а)

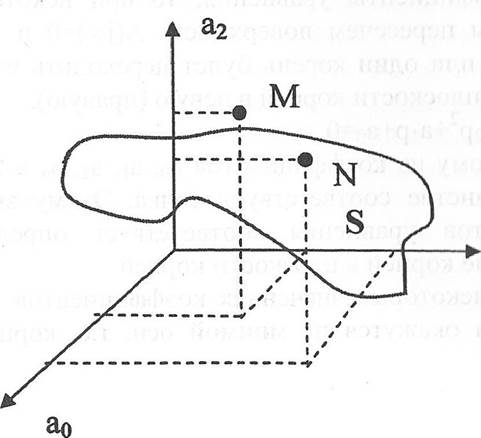
Точке М соответствуют — т], п», тз.

Точке — пь п2, пэ.

Рисунок 2. Поверхность S в пространстве коэффициентов Тразбиение в плоскости 2-х параметров.

При пересечении точкой поверхности корни переходят из одной полуплоскости в другую, следовательно, поверхность S разделяет пространство коэффициентов на области, каждой точке которой соответствует полином третей степени, имеющей определенное количество корней в правой и левой части плоскости корней.

Рассмотрим процедуру построения области устойчивости в плоскости параметров Ко и kl ПИ-регулятора. Передаточная функция ПИ-регулятора имеет вид: ко

                           wp(p) = + —                                                 (7)

Пусть объект регулирования описывается передаточной функцией вида: