Исследование зависимости величины относительного времени безотказной работы иерархической ИИС от величины коэффициента

этом условии трехступенчатая иерархическая система может находиться в семи состояниях.

Тогда время Т₁ безотказной работы системы для этих семи состояний можно определить по формулам:

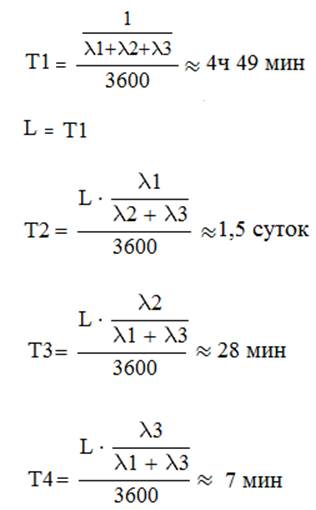
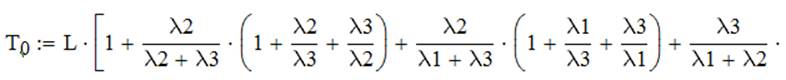
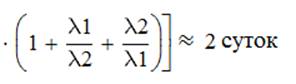
Центральный орган управления представляет собой III ступени иерархии и более надежен, чем объекты нижестоящих ступеней.

Полагаем, что λ₁=аλ₂, λ₂=аλ₃, λ_уо=λ₃ формула имеет вид:

График зависимости относительного времени безотказной работы иерархической ИИС от значения коэффициента а, представлен на рис.4.

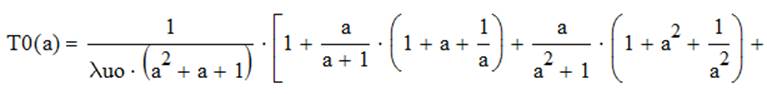
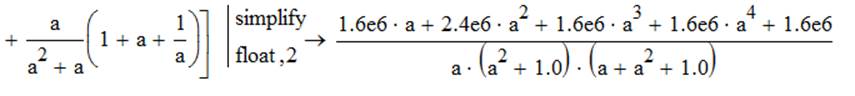
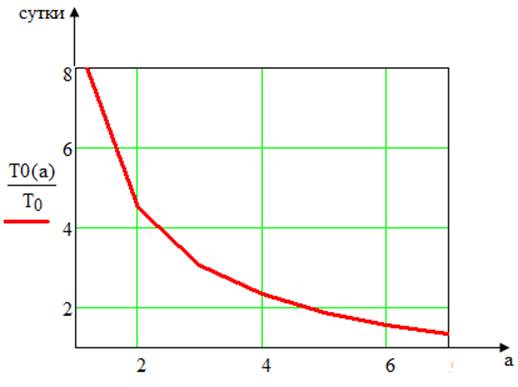
Рис.4. График зависимости относительного времени безотказной работы иерархической ИИС от значения коэффициента а.

Из графика видно, что в промежутке возрастания отказов 1,5>a>2,5, время безотказной работы ИИС снижается в 3 раза. При а>5 время безотказной работы снижается незначительно.

5. Оценка эффективности иерархической ИИС.

Для оценки эффективности иерархической структуры сравним надежность этой структуры с надежностью централизованной системы.

В качестве показателя надежности принимаем вероятность безотказной работы:

где λ – интенсивность отказов системы.

Если в системе имеется n_i объектов управления I ступени, то центральная система содержит n_i линий связи и ЦОУ. Надежность работы этой системы:

где -вероятность безотказной работы ЦОУ;

 - вероятность безотказной работы линий связи.

Иерархическая структура содержит n_по промежуточных объектов и n_пл промежуточных линий связи. Надежность ее работы оценивается выражением:

P_и(t) = P_цо(t)·P_пл^{n пл}(t)·P^{п по}_по(t)

Формально по критерию надежности иерархическая структура эффективна при выполнении условия:

Определим показатели элементов иерархической структуры, при которых условие будет выполняться.

Количество промежуточных линий связи:

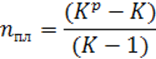
Наибольшей надежностью обладает ЦОУ, поэтому принимается допущение , т.е. интенсивность отказов промежуточных объектов в а раз больше интенсивности отказов ЦОУ.

Из условия  определяются требования к надежности промежуточных объектов и линий связи иерархической структуры:

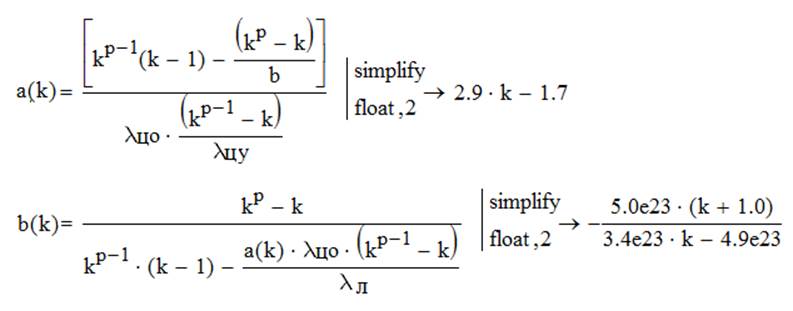
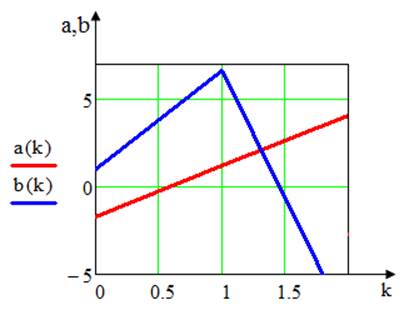
Рис.5. Графики зависимости а=f(k), b=f(k)

Анализ графиков показывает, что при увеличении коэффициента ветвления иерархической структуры параметр a(k) изменяется линейно, а с увеличением числа ступеней р>1  надежность b(k) уменьшается.

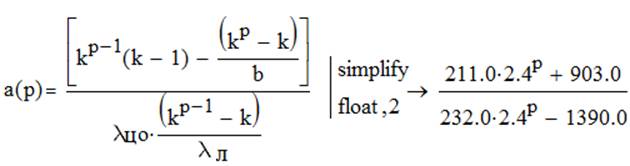
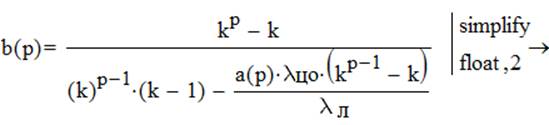
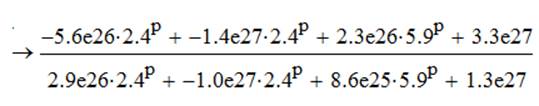
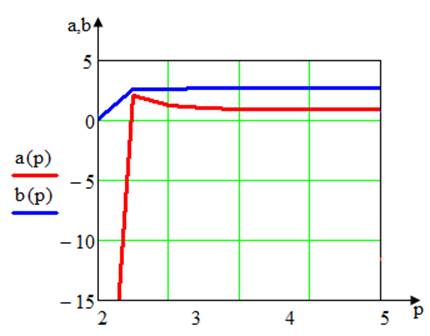
Рис.6. Графики зависимости а=f(p), b=f(p)

Анализ графиков показывает, что при увеличении коэффициента ветвления иерархической структуры снижение требований к надежности промежуточных объектов и линий связи не происходит, а с увеличением числа ступеней надежность промежуточных объектов и линий связи не изменяется.

Заключение

В курсовой работе представленная топология типа ячеистая. Этот тип ячеистой топологии по-прежнему обеспечивает защиту от сбоев для серверов с важной информацией, но не добавляет защиты для отдельных клиентов сети. Гибридная ячеистая топология должна стоить меньше, чем сеть, полностью построенная на ячеистой топологии, но будет не столь защищенной от сбоев. Проведя исследование зависимости величины относительной суммарной длины линий связи от взаимного расположения объектов i и  j ступеней, видно, что для минимизации общей длины связи иерархическая структура, объекты второй ступени должны располагаться как можно ближе к объектам первой ступени.

Заметное возрастание общей длины линий связи начинается при I₂/I₃.

Из графика на рис.3. L(p)/Lm=f(p) видно, что уже четырехступенчатая иерархическая структура дает существенный выигрыш в сокращении суммарной длины линий связи. Дальнейшее увеличение числа ступеней p>4 приводит к возрастанию общего количества узлов, следовательно, снизится надежность ИИС.

Из графика видно, что в промежутке возрастания отказов 1,5>a>2,5, время безотказной работы ИИС снижается в 3 раза. При а>5 время безотказной работы снижается незначительно.

Анализ графиков a(k), b(k) показывает, что при увеличении коэффициента ветвления иерархической структуры параметр a(k) изменяется линейно, а с увеличением числа ступеней р>1  надежность b(k) уменьшается.

Анализ графиков a(p), b(p) показывает, что при увеличении коэффициента ветвления иерархической структуры снижение требований к надежности промежуточных объектов и линий связи не происходит, а с увеличением числа ступеней надежность промежуточных объектов и линий связи не изменяется.

Список используемой литературы

1. Исомин Б.П., Неклюдов С.Ю., Черткова А.А. Вычистительные сети, системы и телекоммуникации: учебник