Построение графика функции по точкам. Построение нескольких графиков в одной системе координат, страница 3

Примечание 3. Функции Im(...) и Re(...) возвращают мнимую и действительную часть комплексного числа соответственно

Примечание 4.  Переменная N  в первой формуле — заданное по варианту количество элементарных RLC-звеньев.

На основе АЧХ можно определить такой параметр как полоса пропускания ЛС. Это непрерывный диапазон частот, внутри которого мощность выходного сигнала не уменьшается ниже некоторого предела. Часто граничными  являются частоты, на которых мощность входного сигнала в два раза превышает мощность выходного (т.е. частоты, где значение АЧХ равно SQRT(0.5)=0.7). Этим критерием мы и будем руководствоваться в лабораторной работе.

При передаче цифровой информации помимо термина «ширина полосы пропускания» используется также термин «пропускная способность линии связи». Эти термины НЕ ВЗАИМОЗАМЕНЯЕМЫ !!!  Основное различие  в том, что «ширина полосы пропускания» ЛС определяется исключительно электротехническими параметрами самой ЛС и не зависит от принятого способа цифрового кодирования. На пропускную же способность, помимо характеристик линии влияет способ физического кодирования передаваемой информации.

Наиболее простым примером иллюстрирующим различия этих терминов служит телефонная линия. При одной и той же полосе пропускания,  физическое кодирование выполняемое модемами для коммутируемых линий обеспечивает пропускную способность не более 100Кбит/с, кодирование выполняемое ADSL-модемами позволяет достичь пропускной способности до нескольких Мбит/с.

Как известно, любой периодический сигнал может быть представлен в виде бесконечной суммы синусоид, частоты которых кратны частоте анализируемого сигнала. Такие  составляющие принято называть гармониками. Амплитуды гармоник дают представление о спектре сигнала.  Чем большее число гармоник делает значительный вклад в форму сигнала, тем более широкой полосой пропускания должна обладать линия связи, чтобы пропустить сигнал без значительных искажений.

Для любого периодического сигнала с периодом 2*T справедливо следующее выражение:

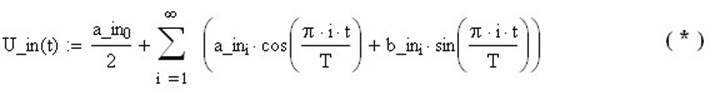
где

i- номера гармоник

a₀ — Величина постоянной составляющей в сигнале

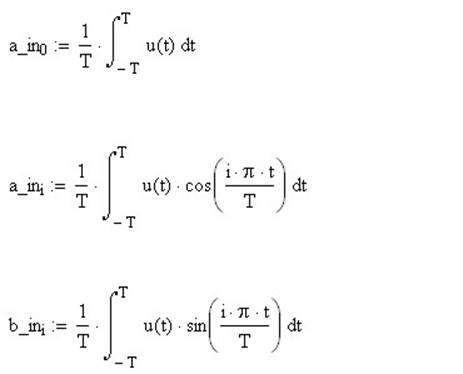
u(t)- функция, описывающая форму сигнала, генерируемого передатчиком.

Примечание 1.  Если функция является кусочно-непрерывной, то либо, интеграл следует брать по каждому участку в отдельности, либо задавать функцию как показано в графике с примером. Поскольку интеграл все равно будете брать не Вы, а программа Mathcad, не стоит бояться громоздкости формул и  расчетов .

Примечание 2.  На практике в формуле (*) рассчитывают не все гармоники, а только первые 10-15 наиболее значимых (у Вас число рассчитываемых гармоник определится в процессе выполнения работы.)

Формула (*) описывает разложенный в ряд Фурье исходный сигнал (т. е. Сигнал, оправленный передатчиком). Сигнал на конце линии связи (т. е. сигнал, принятый приемником) будет искажен в соответствии с параметрами АЧХ и ФЧХ. В частности,  амплитуды i-ой гармоники на выходе ЛС составят:

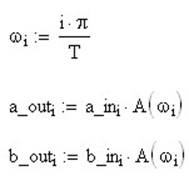
где

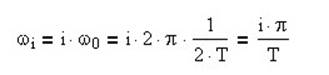
круговая частота i-й гармоники.

Кроме того, в формуле (*) к аргументу синусов и косинусов добавится сдвиг фазы, определяемый по ФЧХ. Соответственно, для выхода ЛС формула (*) примет вид:

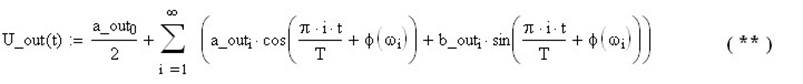
Построив в одной системе координат графики (*) и (**) можно получить наглядное представление об искажении формы сигнала в ЛС с заданными RLC-параметрами.

            2.2.2      Порядок выполнения второй части работы.

•  Создайте новый документ Mathcad (иначе Вам будут серьезно мешать переменные и значения с которыми Вы работали в первой части).