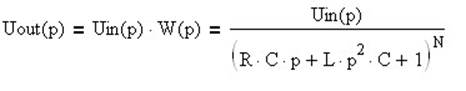
где
Uout(p) - сигнал на выходе ЛC
Uin(p) - сигнал на входе ЛC
N- количество элементарных звеньев цепи (задается вариантом во ВТОРОЙ части лабораторной работы, в первой N=1 для всех вариантов).
Запишите формулу (2) на рабочем листе Mathcad. (“толстый” знак равенства / «булево равно» ставится комбинацией клавиш
Ctrl=
Теперь вам следует получить изображение входного сигнала ()
Скопируйте отдельно выражение для U1(t), выделите в рамку курсора независимую переменную, и выберите пункт меню "Symbolics->Transform->Laplace Transform”.
Ниже выражения для U1(t) во временнОй области Mathcad поместит данное выражение записанное в области операторов Лапласа:
f
![]() (
p2+ f 2)
(
p2+ f 2)
Примечание: В зависимости от версии Mathcad`a оператор Лапласа может быть также обозначен через переменную s. В этом случае Вы должны поправить запись для правильности дальнейших расчетов (и просто ради соблюдения единообразия).
Присвойте в документе Mathcad заданные вам по варианту значения R,L,C.
Переместитесь ниже по документу и скомбинируйте (с помощью операций копированиявставки) последние выражения. У вас получится приблизительно следующая формула:
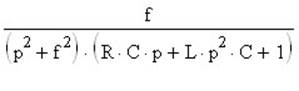
подсветите курсором переменную р (ИСКЛЮЧИТЕЛЬНО ЕЁ!!!) и выберите пункт меню "Symbolics->Transform-> Inverse Laplace Transform” через 3-5 секунд компьютер выдаст Вам выражение, которое будет описывать сигнал на выходе заданной цепи. Поместите его в буфер, а затем определите функцию
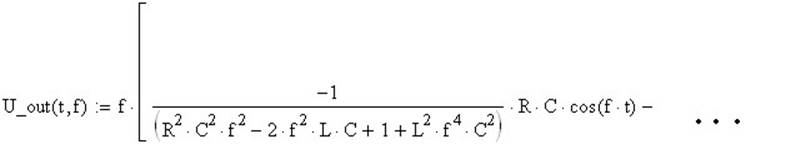
Вставив правую её часть из буфера.
Постройте в одной системе координат два графика U1(t,f) (он же U_in(t,f)) и U_out(t,f). Оцените (визуально) величину затухания и сдвига по фазе (определение точных значений — задача второй части лабораторной работы).
Добавьте в ваш документ Mathcad еще одну систему координат и ней постройте в ней графики: U_out(t,0.125*f), U_out(t,0.25*f), U_out(t,0.5*f), U_out(t,f), U_out(t,2*f), U_out(t,3*f).
Сформулируйте вывод об изменении величины затухания в зависимости от частоты сигнала.
2.2. Анализ изменения импульса заданной формы
Перед выполнением второй части лабораторной работы рекомендуется повторить раздел математики, связанный с рядами Фурье (или хотя бы не полениться и прочитать п.2.2.1.)
2.2.1 Некоторые сведения из теории
В данной лабораторной работе вам предстоит оценить, какой из двух предложенных по варианту способов цифрового кодирования больше подходит для ЛС с заданными RLCпараметрами (а следовательно АЧХ и ФЧХ). Критерием качества линии будет служить рассчитанная Вами пропускная способность.
АЧХ (амплитудно-частотная характеристика) это функция показывающая во сколько раз изменяется амплитуда выходного сигнала ЛС (относительно входного) в зависимости от частоты.
ФЧХ (фазочастотная характеристика) показывает величину сдвига фазы выходного сигнала ЛС (относительно входного) в зависимости от частоты.
АЧХ и ФЧХ очень просто получить из передаточной функции. Для этого следует заменить в ней оператор Лапласа на

|
показатель???? |
После подобной замены у нас получится функция комплексной переменной, АЧХ представляет собой модуль этой функции, ФЧХ —этой функции.
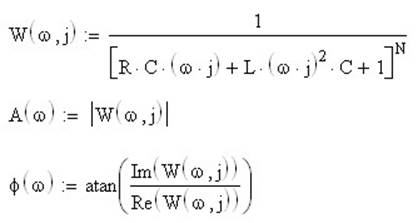
Примечание 1. Разумеется, с точки зрения математики, во всех трёх формулах в правой части в скобках аргументы должны быть записаны в виде произведения, запись их через запятую объясняется особенностями синтаксиса Mathcad.
Примечание 2. Операция взятия модуля записывается в Mathcad с помощью вертикальной черты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.