Строим график "Образцовой" функции. Диапазон изменения времени. Действительный и мнимый спектры сигнала и шума

ПРИМЕР ВЫПОЛНЕНИЯ  ЛАБОРАТОРНОЙ РАБОТЫ №3.

ВНИМАНИЕ!

Комментарии написанные мелким курсивным шрифтом в отчете  присутствовать не должны. Они либо  являются ультрапрописными истинами, либо описывают последовательность действий по выполнению работы.

Задаем начальные условия для выполнения работы:

T := 20 10⋅ ^{− 5}      Uplus := 2       Uminus := −3

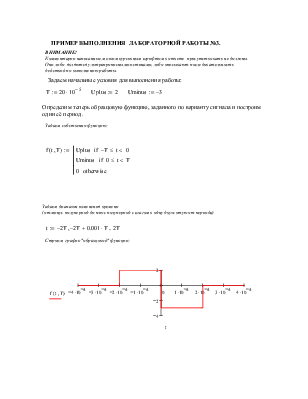
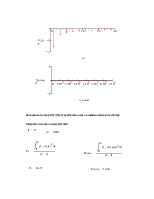
Определим теперь образцовую функцию, заданного по варианту сигнала и построим один её период.

Задаем собственно функцию:

     f t T( ,   ) :=Uplus if −T ≤ t < 0

Uminus if 0 ≤ t < T

0 otherwise

Задаем диапазон изменения времени

(от минус полупериод до плюс полупериод с шагом в одну двухсотую от периода)

t := −2T,−2T + 0.001 ⋅ T.. 2T

Строим  график "образцовой" функции:

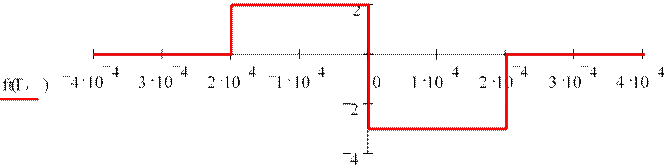
t

Зададим число отображаемых гармоник сигнала U_in,

Gmax := 20         i := 0.. Gmax

Запишем формулы для расчёта коэффициентов этих гармоник.

При этом обратим внимание на справедливость следующих выражений

где

a и  b  - произвольные числа т.е. При симметричных пределах интегрирования коэффициенты при гармониках не будут зависеть от численного значения периода сигнала.

Поскольку Mathcad определенные интегралы берёт численными методами, нам удобнее задать условный полупериод Т1, и интегрировать пределах. от -Т1 до Т1

В противном случае могут возникнуть сложности с расчетом коэффициентов гармоник с большими номерами

T1 := 1

1

a_in0 := T1 ⋅ ⌠⌡−T1 f t T1( ,            ) dt      a_ini := 1 ⋅ ⌠T1  f t T1( ,  ) ⋅ cosi⋅T1π ⋅ t dt

T1                                         T1

⌡− T1

⌠T1

b_ini :=  ¹ ⋅ ^     f t T1( ,          ) ⋅ _sin_ ⁱ⋅T1π ⋅ ^t dt T1

⌡− T1

Маткад их уже подсчитал. Выводить их на экран мы не будем.

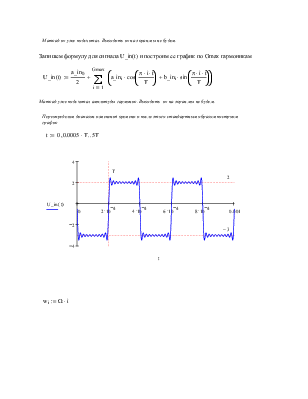
Запишем формулу для сигнала U_in(t) и построим ее график по Gmax гармоникам

Gmax

U_in(t) := a_in0 + ∑ a_ini ⋅ cos π ⋅ i⋅ t + b_ini ⋅ sin π ⋅ i⋅ t

2                  T   T  i = 1

Маткад уже подсчитал амплитуды гармоник. Выводить  их на экран мы не будем.

Переопределим диапазон изменения времени и после этого стандартным образом построим график t := 0 0.0005, ⋅ T.. 5T

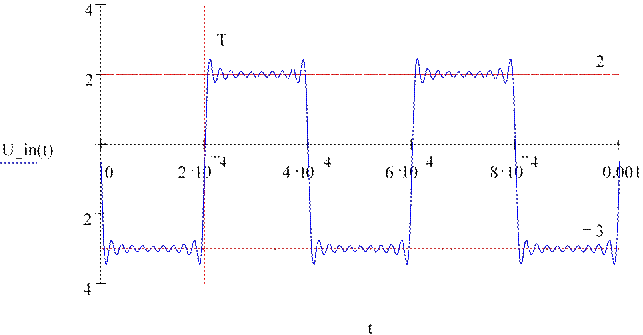
w_i := Ω ⋅ i

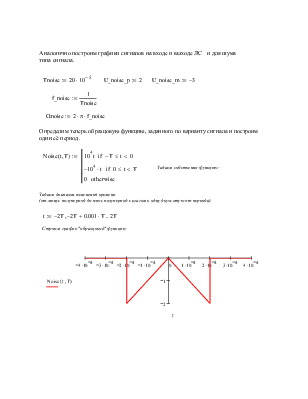
Аналогично построим графики сигналов на входе и выходе ЛС   и для шума типа сигнала.

Tnoise := 20 10⋅  ^{− 5}        U_noise_p := 2       U_noise_m := −3

f_noise := ¹

Tnoise

Ωnoise := 2 ⋅ π ⋅ f_noise

Определим теперь образцовую функцию, заданного по варианту сигнала и построим один её период.

Noise t T( ,    ) :=10⁴t if −T ≤ t < 0

−10⁴ ⋅ t if 0 ≤ t < T               Задаем собственно функцию:

0 otherwise

Задаем диапазон изменения времени

(от минус полупериод до плюс полупериод с шагом в одну двухсотую от периода)

t := −2T,−2T + 0.001 ⋅ T.. 2T

Строим  график "образцовой" функции:

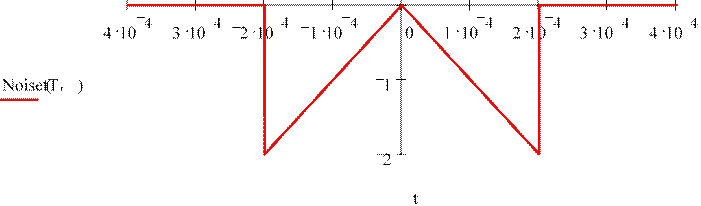
¹           ⌠Tnoise a_noise0 := ⋅      Noise t Tnoise( ,        ) dt

Tnoise   ^⌡− Tnoise

⌠Tnoise

1      

a_noisei := ⋅           Noise t Tnoise( , ) ⋅ cosTnoisei⋅ π ⋅ t  dt

Tnoise ⌡− Tnoise

Tnoise

¹ ⌠^ Noise t Tnoise( , ) ⋅ sin^{ i}⋅ π ⋅ ^t ^ dt b_noise_i := Tnoise ⋅ ⌡− Tnoise _Tnoise

Запишем формулу для сигнала U_noise(t) и построим ее график по 20 гармоникам

Gmax

U_noise(t) := a_noise⁰ + ∑ a_noise_i ⋅ _cos π ⋅ ⁱ⋅ ^t  + _{b_noisei} ⋅ _sin π ⋅ ⁱ⋅ ^t 

2       Tnoise     Tnoise

i = 1

Маткад уже подсчитал амплитуды гармоник. Выводить  их на экран мы не будем.

w_noisei := Ωnoise i⋅

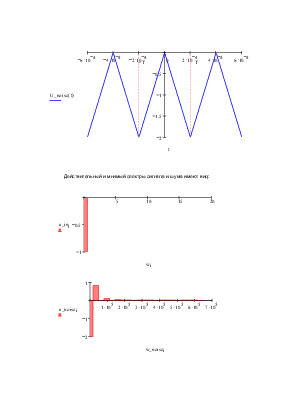
Переопределим диапазон изменения времени и после этого стандартным образом построим график t := −3Tnoise,−3Tnoise + 0.0005 ⋅ Tnoise.. 3Tnoise

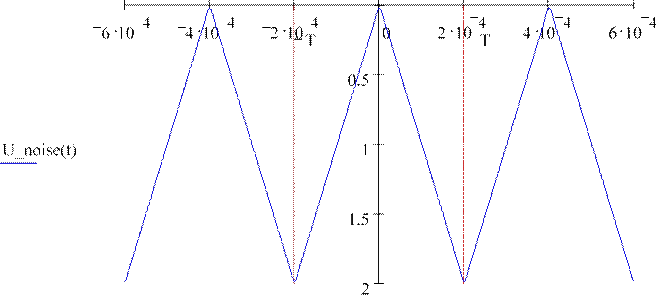
t

Действительный и мнимый спектры сигнала и шума имеют вид:

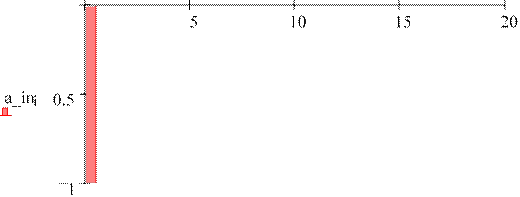
wi

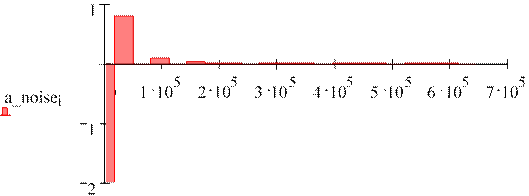
w_noisei

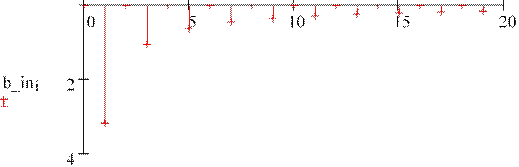
wi

Как видим в сигнале отсутствует действительная, а в шуме мнимая часть спектра