Теория графов – это математический язык для формализации понятий, связанных с анализом и синтезом структур объектов, систем и процессов.
Теория графов – самостоятельный раздел дискретной математики, который включает алгебру графов, алгоритмическую теорию графов (построение различных объектов на графе), прикладную теорию графов (применение теории графов для решения конкретных задач).
Возникновение теории графов принято датировать 1936 годом, когда появилась книга Денеша Кёнига «Теория конечных и бесконечных графов». Однако отдельные задачи по теории графов возникали и решались много раньше, например, Леонард Эйлер (1707 – 1782) в 1736 году сформулировал задачу о Кенигсбергских мостах:
Можно ли обойти все участки суши и вернуться к исходной точке, пройдя один раз по каждому мосту? (Два острова, семь мостов.)
 С
С А D
B
Области применения теории графов: Химия. Химическая информатика. Электротехника. Электроника. Молекулярная биология (ДНК). Психология. Социология. Программирование. Информатика и многие многие другие.
Классификация графов
|
Признак классификации |
Графы |
|
Ориентация (может быть или нет) |
– орграф – неорграф – смешанный граф |
|
Взвешенность: структурная или функциональная |
– взвешенный функцией – невзвешенный граф – частично взвешенный |
Виды весов: Тип взвешенности:
–арифметические числа – реберная
–функции – вершинная
–логические – смешанный вариант
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
![]() X – множество вершин графа, |X| = n,
X – множество вершин графа, |X| = n,
E – множество ребер графа, |E| = m. E: X![]() X.
X.
![]() Совокупность
множества Х вершин и множества Е связей между ними называется графом и обозначается
G(X,E).
Совокупность
множества Х вершин и множества Е связей между ними называется графом и обозначается
G(X,E).
Пример: Все графы на 4 вершинах. G(X, E), где |X|=4.
Если у какой-либо вершины в графе нет ребер, то это граф с изолированной вершиной.
(Обратите внимание на обозначения C4, P4, K4 – цикл, цепь, полный граф с четырьмя вершинами)!!!
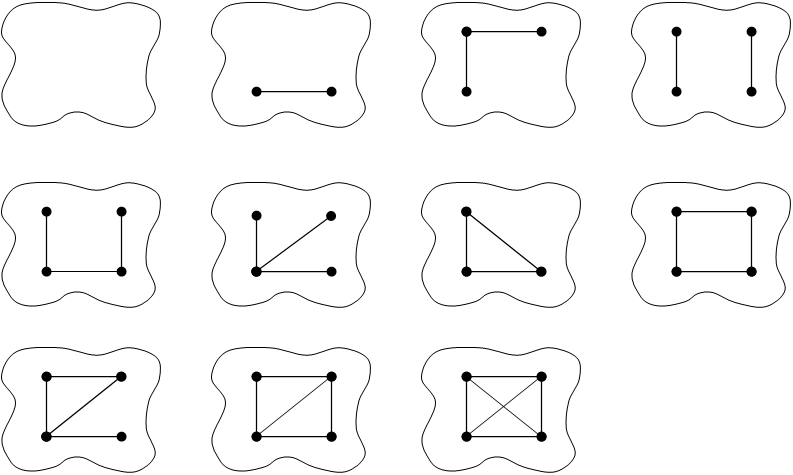
1 2 1 2
3 4
G1(4,0) G2 G3 G4
G5 цепь P4 G6 G7 G8 (4,4) цикл C4
G9 G10 G11
полный граф K4
![]()

 x1
x1
![]() e4 G(4,6)
e4 G(4,6)
e2

![]() x4
x4
![]()
 x2 e6
x2 e6
![]()
e5 e3 x2
![]() Если связь
имеет направление, то она называется дугой, в противном случае – ребром.
Если связь
имеет направление, то она называется дугой, в противном случае – ребром.
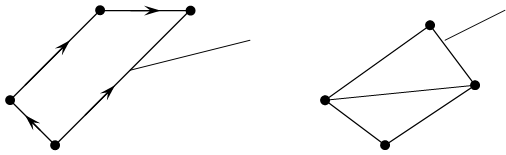 ребро e
ребро e
дуга e
![]() Граф,
у которого все связи являются ребрами, называется неографом.
Граф,
у которого все связи являются ребрами, называется неографом.
 e4
e4
e6 e1
e5
e3 e2
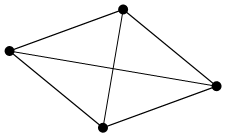
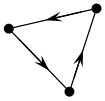
![]() Граф
с дугами называется ориентированным графом (орграфом).
Граф
с дугами называется ориентированным графом (орграфом).
e3
 |
e2 e1
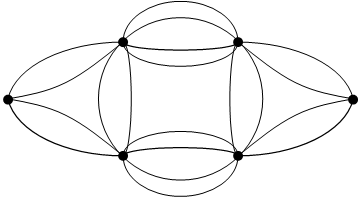
![]() Если
у графа существуют кратные ребра, т.е. несколько ребер, соединяющих одну и туже
пару вершин, то такой граф называются мультиграфом.
Если
у графа существуют кратные ребра, т.е. несколько ребер, соединяющих одну и туже
пару вершин, то такой граф называются мультиграфом.
![]() e1
e1
![]() а в e2
а в e2
![]() мультиграф
G(6,20)
мультиграф
G(6,20)
 e3
e3
e4
а, в – 2 вершины графа;
e1,e2,e3,e4 – кратные ребра, соединяющие вершины а и в.
![]() Ребро,
оба конца которого связаны с одной и той же вершиной, называется петлей.
Ребро,
оба конца которого связаны с одной и той же вершиной, называется петлей.
 Петля
Петля
![]()
![]() Вершина
Вершина
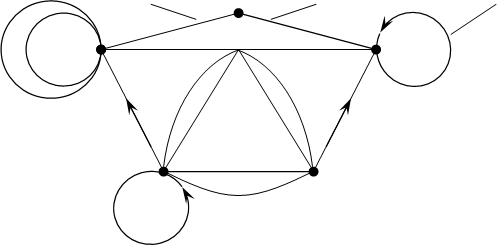
![]() Граф
называется псевдографом, если множество Е включает ребра, дуги, петли и все они
могут быть кратными.
Граф
называется псевдографом, если множество Е включает ребра, дуги, петли и все они
могут быть кратными.
дуга e9 дуга e8 петля e1
 |
![]() ребро e5 ребро
e6
ребро e5 ребро
e6
 |

![]() дуга e3
дуга e3
![]()
![]()
![]() петля e6
дуга e2
петля e6
дуга e2
 петля e7
петля e7
![]()
 дуга
e4 кратные
дуга
e4 кратные
![]()
 ребро e3
ребро e3
![]() ребро e4 ребро
e2
ребро e4 ребро
e2
![]() петля e5 ребро e2 кратные
петля e5 ребро e2 кратные
![]() Две
вершины называются смежными, если они соединяются некоторым ребром (дугой)
графа, и два различные ребра (дуги) смежны, если они имеют общую вершину.
Две
вершины называются смежными, если они соединяются некоторым ребром (дугой)
графа, и два различные ребра (дуги) смежны, если они имеют общую вершину.
a e1 b
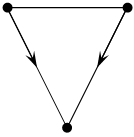 |
e3 e2
c
![]() Вершина
хi инцидентна дуге (ребру) еij,
если она является началом или концом дуги (ребра).
Вершина
хi инцидентна дуге (ребру) еij,
если она является началом или концом дуги (ребра).
1 e12 2
х1 инцидентна дуге е12, так как х1 начало е12.
х2 инцидентна дуге е12, так как х2 конец е12.
![]() Дуга
(ребро) еij инцидентна вершине xi, если она выходит из этой вершины или входит в нее.
Дуга
(ребро) еij инцидентна вершине xi, если она выходит из этой вершины или входит в нее.

 x1
x1
e12 инцидентна xi.
e12
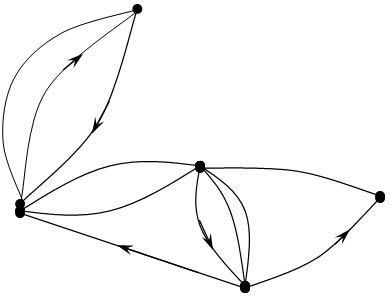
![]() Число
ребер (дуг), инцидентных некоторой вершине хi, называют
степенью вершины (обозначение deg(xi)).
Число
ребер (дуг), инцидентных некоторой вершине хi, называют
степенью вершины (обозначение deg(xi)).
 x5
x5
e11
e10
e9
e7 x1 e5
e8 x4
e2 e1
e6
e4
x2
Например степень вершины: x1:6;
(ребра е7, е8, е2, е1, е5, дуга е7), степень вершины X5:3;
(ребро e11, дуга e7 и т.д.)
![]() Для
неорграфа сумма степеней вершин равна удвоенному числу его ребер:
Для
неорграфа сумма степеней вершин равна удвоенному числу его ребер: 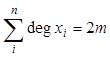 .
.
x1 e1 x2 Ст. свободы x1: 2
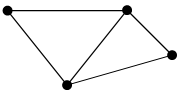 Ст.
свободы x2:
3
Ст.
свободы x2:
3
e4 e2 Ст. свободы x3: 2
e5 x3 Ст. свободы x4: 3
e3
x4
Неорграф G(4,5)
Сумма степеней вершин: S=2+3+2+3=10. Количество ребер n=5 (e1, e2, e3, e4, e5). S=2n=2∙5=10.
![]() Для
орграфа вводится понятие полустепени исхода (deg+) и полустепени захода (deg-) вершины, что соответствует числу выходящих и
входящих дуг соответственно.
Для
орграфа вводится понятие полустепени исхода (deg+) и полустепени захода (deg-) вершины, что соответствует числу выходящих и
входящих дуг соответственно.
полустепень исхода вершины е: 1
(одна выходящая дуга 10)
полустепень захода вершины е: 3
(3 входящие дуги :4,7,9)
полустепень исхода вершины а: 2
(2 выходящие дуги: 1, 2)
полустепень захода вершины а: 1
(одна заходящая дуга 10)
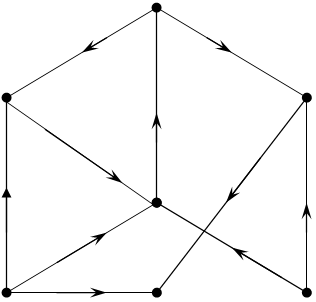 a
a
1 2 Орграф G(7,10)
g b
10
9
8 e
5 3
7
4
f 6 d c
![]() Граф, в котором
перемещаясь от вершины к вершине по дугам, можно попасть в каждую вершину,
называется связным, в противном случае граф называется несвязным.
Граф, в котором
перемещаясь от вершины к вершине по дугам, можно попасть в каждую вершину,
называется связным, в противном случае граф называется несвязным.
 а b b c
а b b c

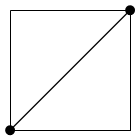

 a d
a d
f e
d c
Связный граф G1(4,5) Несвязнй граф G2(6,4)
Несвязный граф G2(6,4) состоит из двух компонент.
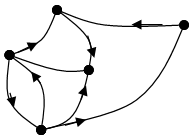
![]() Маршрутом
в графе называют чередующуюся последовательность вершин и ребер (дуг), которая
начинается и заканчивается вершиной.
Маршрутом
в графе называют чередующуюся последовательность вершин и ребер (дуг), которая
начинается и заканчивается вершиной.
e
 e6 d
e6 d
b e4 e5
e3 c
e2 e8 e7
e1
a
G(5, 8)
Маршрут из точки “a” в “b” (а – начальная вершина, b – конечная вершина): последовательность дуги e7, вершины d, дуги e6, вершины e, дуги e5, вершины c, дуги e3.
Маршрут называется цепью, если все его ребра (дуги) различны и простой цепью, если все его вершины различны.
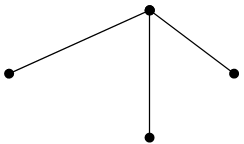
![]() Замкнутый
маршрут называется циклом (контуром), если все его вершины и ребра (дуги)
различны и его длина l>2. Цикл (контур) называется простым, если
все его вершины различны.
Замкнутый
маршрут называется циклом (контуром), если все его вершины и ребра (дуги)
различны и его длина l>2. Цикл (контур) называется простым, если
все его вершины различны.
b
 |
e4 e1

 a e5 c
a e5 c
e3 e2
d
Маршрут b–e1–c–e2–d–e5–b является замкнутым и его вершины (b,c,d) и ребра (e1, e2, e5) различны, а длина маршрута равна l=3, следовательно данный маршрут можно назвать простым циклом.
![]() Вершина
графа, после удаления которой увеличивается число компонент
Вершина
графа, после удаления которой увеличивается число компонент
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.