УДК ???.???
Чирков А.В. Компьютерная графика. Учебное пособие. Часть II. – М.: МГАПИ, 2005. – 21 с.; ил.
Настоящее учебное пособие предназначено для подготовки студентов III – V курсов различных форм обучения по специальности 22.01 «Вычислительные машины, комплексы, системы и сети» по дисциплине «Компьютерная графика». Пособие может использоваться студентами при выполнении лабораторных и практических работ.
Рецензент: ?????????????
Учебное пособие одобрено на заседании кафедры ИТ-4 «___» января 2005 г., протокол № ____.
Зав. каф. ИТ-4 д.т.н., профессор __________
ÓМГАПИ, 2005
СОДЕРЖАНИЕ
ВВЕДЕНИЕ..................................................................................... 5
1. РАСТРОВЫЕ АЛГОРИТМЫ ВЫВОДА ПРИМИТИВОВ НА ЭКРАН...................................................................................................... 6
1.1. Растровые алгоритмы.......................................................... 6
1.2 Вывод на экран произвольной точки................................... 6
1.3 Растровое представление отрезка. Алгоритм Брезенхейма 6
1.4 Алгоритм построения однородного треугольника............. 7
2. РАСЧЁТ ОСВЕЩЁННОСТИ. МОДЕЛИ ЗАЛИВКИ ПОВЕРХНОСТИ. МЕТОД ГУРО............................................................ 9
2.1 Расчет освещенности............................................................ 9
2.2 Растровые алгоритмы закрашивания треугольника. Закраска треугольника методом Гуро................................................. 9
3. НАЛОЖЕНИЕ ТЕКСТУР НА ПОВЕРХНОСТЬ.................... 12
4. ПАРАЛЛЕЛЬНАЯ И ПЕРСПЕКТИВНАЯ ПРОЕКЦИИ. РАБОТА С ПРОИЗВОЛЬНОЙ КАМЕРОЙ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ................................................................................... 14
4.1 Параллельная проекция...................................................... 14
4.2 Перспективная проекция.................................................... 14
4.3 Работа с произвольной камерой......................................... 14
4.4 Алгоритм художника.......................................................... 17
5. ОТСЕЧЕНИЯ НЕВИДИМЫХ ГРАНЕЙ................................. 19
5.1. Отброс нелицевых граней................................................. 19
5.2 Расчет нормали к объекту.................................................. 19
5.3 Удаление невидимых граней. Метод z-буфера................. 20
СПИСОК ЛИТЕРАТУРЫ............................................................ 22
Преобразование идеального объекта в растровое представление одна из наиболее важных задач, которые приходится решать в компьютерной графике. Простейшим примитивом в данном случае является точка, которую необходимо вывести на экран. Экран, в свою очередь, в современных устройствах графического отображения информации представлен в виде линейного участка оперативной памяти, заданного своими размерами и глубиной цвета. В первом разделе студент знакомится с выводом как простейших двумерных примитивов, таких как точка и отрезок, так и более сложных, представляющих собой однородные замкнутые контуры.
В современной компьютерной графике, кроме работы с двумерными примитивами, всё чаще применяется трехмерное изображение, состоящее из совокупности трехмерных объектов, объединённых в сцену. Для придания им реалистичности применяются специальные методы расчёта освещённости граней и придания им вида реальных объектов засчёт использования текстур. Этим вопросам посвящены второй и третий разделы учебного пособия.
Современное аппаратное обеспечение обогатилось засчёт использования трехмерных дисплеев и проекторов, но в настоящее время парк двумерных дисплеев составляет наибольшую часть, используемых устройств отображения. Для вывода на двумерные дисплеи трехмерных сцен используются методы параллельного и перспективного проецирования. Их использованию посвящён четвёртый раздел учебного пособия.
Пятый раздел учебного пособия знакомит студентов с методами отсечения невидимых граней, которые применяются для ускорения вывода трехмерной сцены и вывода объектов в правильном порядке.
Предлагаемое учебное пособие ориентировано на проведение экспериментов с использованием ЭВМ и требует от студентов наличия навыков программирования на языках высокого уровня.
В подавляющем большинстве графические устройства являются растровыми, т.е. изображение представляет собой прямоугольную матрицу (сетки, целочисленной решетки) точек (растра), поэтому возникает необходимость в растровых алгоритмах.
Хотя большинство графических библиотек содержат внутри себя достаточное количество простейших растровых алгоритмов, таких как:
· переведение идеального объекта (отрезка, окружности и др.) в их растровые образы;
· обработка растровых изображений, тем не менее, часто возникает необходимость явного построения растровых алгоритмов.
Растровое представление экрана представляет собой сетку размером SizeX точек по горизонтали и SizeY точек по вертикали. Мы будем рассматривать дисплей, каждая точка которого состоит из трех цветов (Red, Green, Blue), где каждая компонента цвета может иметь 256 градаций яркости (от 0 до 255) и занимает 1 байт. Т.о. одна точка занимает 3 байта. Объем памяти, занимаемый изображением равен X*Y*3.
При разрешении 640*480 мы имеем изменение по горизонтали от 0 до 639 и по вертикали от 0 до 479. Чтобы нарисовать произвольную точку, необходимо использовать следующую формулу:
p = (SizeX*Y + X)*3, где X, Y – координаты рисуемой точки;
p – смещение точки в памяти.
В 1965 году Брезенхеймом был предложен простой
целочисленный алгоритм для растрового построения отрезка, первоначально
предназначенный для использования в графопостроителях.
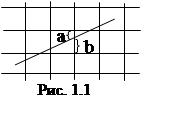
При построении растрового изображения отрезка всегда выбирается ближайшая по вертикали точка. При этом из двух точек A(x1, y1) и B(x2, y2) (рис. 1) выбирается та, которая ближе к исходной прямой (в данном случае выбирается точка A, т.к. a < b). Для этого вводится число d, равное (x2 – x1)*(b - a).
В случае d > 0 значение y от предыдущей точки увеличивается
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
