


Часть 2. Дифференцирование.
Контрольная работа
№2. Цель данной контрольной
работы помочь студентам в овладении навыками нахождения производных функций
одной переменной. Операция нахождения производной называется дифференцированием
функции. Производная функции y=f(x) обозначается либо ![]() ,
либо
,
либо ![]() .
.
Сформулируем основные правила дифференцирования и приведем формулы производных основных элементарных функций:
1. ![]() 10.
10. ![]()
2.![]() 11.
11. ![]()
3. 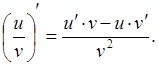 12.
12. 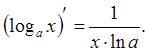
4. ![]() 13.
13. 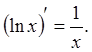
5. ![]() 14.
14. 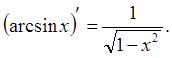
6. ![]() 15.
15. 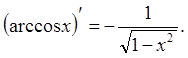
7. ![]() 16.
16. 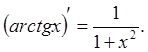
8. 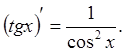 17.
17. 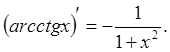
9. 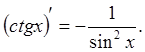
Отметим, что полезно запомнить частный случай формулы 5
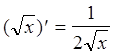 .
.
Большое значение для вычисления производных различных функций имеет следующая теорема:
Теорема о
производной сложной функции.
Пусть ![]() где
где ![]() ,
тогда
,
тогда
![]()
или эта формула записывается в виде
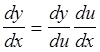
Так, например, если ![]() , то формулы 5, 6, 10, 13
принимают вид:
, то формулы 5, 6, 10, 13
принимают вид:
5а. ![]()
6а. ![]()
10а. ![]()
13а. 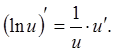
Задача 1a.
Основная цель данной задачи проверить навыки дифференцирования сложной функции. Рассмотрим примеры.
Найти ![]() , где
, где ![]() .
.
Приведем подробное решение этой задачи. (Мы предполагаем, что студенты к моменту выполнения контрольной работы изучили таблицу производных основных элементарных функций.)
Функция имеет вид ![]() , где
, где ![]() .
.
Воспользуемся формулой производной сложной функции. Тогда
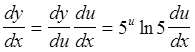 , где
, где ![]() .
Функция u(x) имеет вид
.
Функция u(x) имеет вид ![]() , где
, где ![]() . Получаем
. Получаем 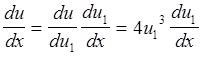 . Функция
. Функция ![]() имеет вид
имеет вид ![]() , где
, где ![]() . Получаем
. Получаем 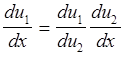 =
=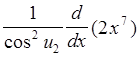 =
=
=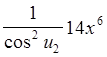 .
.
Теперь можем записать окончательный ответ
Ответ: ![]() =
=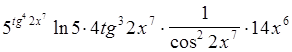 .
.
Отметим, что нет необходимости (если вы уверенно владеете техникой дифференцирования) при выполнении контрольной работы столь подробно проводить все выкладки.
Задача. Найти ![]() , где
, где ![]() .
.
Используя последовательно формулы 10, 5, 6, 4 и 5, а также правило дифференцирования сложной функции, получим:
![]() =
=![]()
=![]() .
.
Отметим, что все производные по промежуточным аргументам можно выполнять в уме и непосредственно давать готовый ответ.
Задача. Найти ![]() , где
, где ![]() .
.
Ответ: 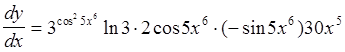 .
.
Задача 1б.
Целью данной задачи является закрепления навыков нахождения производной произведения функций.
Задача. Найти ![]() , если
, если ![]() .
.
Используя формулу производной произведения, получаем
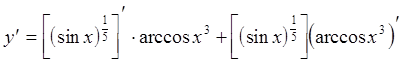 .
.
Далее воспользуемся формулой производной сложной функции. Получаем
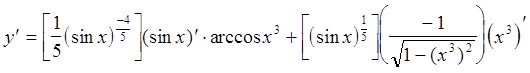 .
.
Вычисляя табличные производные, получаем ответ.
Ответ:
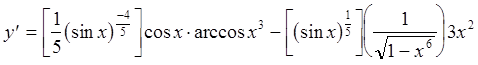 .
.
Как мы уже упоминали ранее, при уверенном владении техникой дифференцирования в контрольной работе нет необходимости приводить столь подробное описание.
Рассмотрим еще один пример.
Задача. Найти ![]() , если
, если ![]()
Сначала воспользуемся формулой производной произведения, а затем формулой дифференцирования сложной функции:
![]() =
=![]() =
=
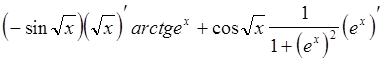 =
=
=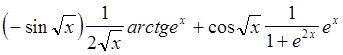 .
.
Приведем решение еще одного примера, где все промежуточные рассуждения проведены в уме.
Задача. Найти ![]() , если
, если ![]() .
.
![]() =
=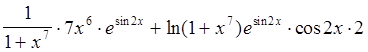
Задача 1в.
Целью данной задачи является закрепления навыков нахождения производной частного.
Задача. Найти ![]() , если
, если 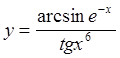 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.