Задача 1
1. Составьте таблицу истинности, СДНФ и СКНФ функции трех переменных, заданной номерами единичных наборов, получите минимальные ДНФ и КНФ этой функции двумя способами:
а) используя законы и тождества булевой алгебры;
б) используя карту Карно.
Номер строки варианта функции выбирается по номеру в журнале группы.
2. Реализуйте функцию п. 1 на элементах: а) И, ИЛИ, НЕ; б) И–НЕ;
в) ИЛИ–НЕ.
3. Проверьте правильность работы полученных схем моделированием.
|
№ |
Вариант 1 |
Вариант 2 |
№ |
Вариант 1 |
Вариант 2 |
|
|
1 |
0156 |
0134 |
16 |
0457 |
1234 |
|
|
2 |
0124 |
0157 |
17 |
1245 |
1256 |
|
|
3 |
0135 |
0146 |
18 |
1267 |
1235 |
|
|
4 |
0125 |
0147 |
19 |
1246 |
1257 |
|
|
5 |
0137 |
0126 |
20 |
1236 |
0167 |
|
|
6 |
0136 |
0127 |
21 |
1237 |
1345 |
|
|
7 |
0234 |
0245 |
22 |
1356 |
1367 |
|
|
8 |
0256 |
0267 |
23 |
1346 |
3457 |
|
|
9 |
0235 |
3467 |
24 |
1347 |
1356 |
|
|
10 |
0257 |
0236 |
25 |
1367 |
3456 |
|
|
11 |
0247 |
0237 |
26 |
1456 |
1467 |
|
|
12 |
0345 |
0567 |
27 |
1457 |
2345 |
|
|
13 |
0367 |
0346 |
28 |
2356 |
2367 |
|
|
14 |
0357 |
0347 |
29 |
2346 |
2357 |
|
|
15 |
0456 |
0467 |
30 |
2347 |
2456 |
Задача 2
Разработайте и проверьте моделированием логическую схему для реализации частично определенной логической функции F четырех аргументов, заданной номерами единичных и нулевых наборов.
Вариант выбирается по номеру в журнале группы.
|
Группа 1 |
Группа 2 |
|||||
|
№ |
Наборы |
№ |
Наборы |
|||
|
единичные |
нулевые |
единичные |
нулевые |
|||
|
1 |
3,6,7,9,11 |
1,2,4,8,12 |
1 |
2,8,9,10,13 |
0,5,6,7,12 |
|
|
2 |
2,4,6,7,15 |
0,5,8,10,13 |
2 |
0,4,5,13,15 |
1,2,7,10,11 |
|
|
3 |
2,3,6,12,14 |
1,4,7,9,13 |
3 |
0,1,4,12,14 |
3,6,7,11,15 |
|
|
4 |
2,3,7,8,10, |
0,5,6,12,13 |
4 |
2,3,6,9,11 |
1,4,7,12,13 |
|
|
5 |
1,9,11,14,15 |
0,3,4,6,10 |
5 |
0,8,10,14,15 |
1,2,5,7,11 |
|
|
6 |
5,10,13,14,15 |
0,1,2,7,11 |
6 |
4,11,12,14,15 |
0,1,3,6,10 |
|
|
7 |
4,10,11,12,14 |
1,3,5,6,15 |
7 |
5,10,11,13,15 |
0,2,4,7,14 |
|
|
8 |
0,8,10,11,15 |
2,4,5,6,14 |
8 |
1,9,10,11,14 |
3,4,5,6,15 |
|
|
9 |
1,4,5,9,11 |
0,3,6,10,14 |
9 |
0,4,5,8,10, |
1,2,7,11,15 |
|
|
10 |
0,4,5,13,15 |
1,2,7,10,11 |
10 |
1,4,5,12,14 |
0,3,5,10,11 |
|
|
11 |
0,1,4,12,14 |
3,6,7,11,15 |
11 |
0,1,5,13,15 |
2,4,7,10,14 |
|
|
12 |
0,1,4,12,14 |
2,4,7,14,15 |
12 |
0,1,4,9,11, |
3,5,6,14,15 |
|
|
13 |
3,9,11,12,13 |
1,2,4,6,8, |
13 |
3,6,7,9,11 |
1,2,4,8,12 |
|
|
14 |
7,8,12,13,15 |
0,2,3,5,9 |
14 |
2,4,6,7,15 |
0,5,8,10,13 |
|
|
15 |
6,8,9,12,14 |
0,1,4,7,13 |
15 |
2,3,6,12,14 |
1,4,7,9,13 |
|
|
16 |
2,3,7,13,15 |
0,5,6,8,12 |
16 |
2,6,7,8,10 |
0,3,5,9,13 |
|
|
17 |
2,6,7,8,10 |
0,3,5,9,13 |
17 |
3,6,7,12,14 |
1,2,4,8,9 |
|
|
18 |
3,6,7,12,14 |
1,2,4,8,9 |
18 |
2,3,7,13,15 |
0,5,6,8,12 |
|
|
19 |
2,3,7,13,15 |
0,5,6,8,12 |
19 |
1,4,5,12,14 |
0,3,5,10,11 |
|
|
20 |
2,3,6,9,11 |
1,4,7,12,13 |
20 |
0,1,5,13,15 |
2,4,7,10,14 |
|
|
21 |
0,8,10,14,15 |
1,2,5,7,11 |
21 |
2,6,7,8,10, |
0,3,5,9,13 |
|
|
22 |
4,11,12,14,15 |
0,1,3,6,10 |
22 |
3,6,7,12,14 |
1,2,4,8,9 |
|
|
23 |
5,10,11,13,15 |
0,2,4,7,14 |
23 |
2,3,7,13,15 |
0,5,6,8,12 |
|
|
24 |
1,9,10,11,14 |
3,4,5,6,15 |
24 |
0,8,10,11,15 |
2,4,5,6,14 |
|
|
25 |
0,4,5,8,10, |
1,2,7,11,15 |
25 |
0,1,4,12,14 |
2,4,7,14,15 |
|
|
26 |
1,4,5,12,14 |
0,3,5,10,11 |
26 |
3,9,11,12,13 |
1,2,4,6,8, |
|
|
27 |
0,1,5,13,15 |
2,4,7,10,14 |
27 |
2,3,7,8,10, |
0,5,6,12,13 |
|
|
28 |
0,1,4,9,11, |
3,5,6,14,15 |
28 |
1,9,11,14,15 |
0,3,4,6,10 |
|
|
29 |
2,6,7,8,10, |
0,3,5,9,13 |
29 |
5,10,13,14,15 |
0,1,2,7,11 |
|
|
30 |
3,6,7,12,14 |
1,2,4,8,9 |
30 |
4,10,11,12,14 |
1,3,5,6,15 |
|
|
31 |
2,3,7,13,15 |
0,5,6,8,12 |
31 |
2,3,6,9,11, |
1,4,7,12,13 |
|
Задача 3
Разработайте и проверьте моделированием логическую схему, реализующую систему трех логической уравнений F1, F2, F3 четырех аргументов, заданных номерами единичных наборов.
Вариант выбирается по номеру в журнале группы.
|
СИНТЕЗ МНОГОВЫХОДНЫХ КОМБИНАЦИОННЫХ СХЕМ |
|||
|
Группа 1 |
|||
|
Вариант |
F1(x4,x3,x2,x1) |
F2(x4,x3,x2,x1) |
F3(x4,x3,x2,x1) |
|
1 |
0,1,2,3,6,8,9,14 |
0,1,4,6,8,9,15 |
0,2,8,9,10,15 |
|
2 |
1,2,4,5,8,12,13 |
0,3,7,8,9,12,13 |
1,4,5,8,10,11 |
|
3 |
0,1,3,4,6,9,11,14 |
1,3,9,11,12,13,14 |
0,1,8,10,12,13 |
|
4 |
0,1,6,7,8,9,12,14 |
2,6,7,10,11,12,14 |
0,1,5,6,12,14 |
|
5 |
1,3,4,7,8,12,14,15 |
2,4,7,8,10,12,15 |
2,4,8,10,12,14 |
|
6 |
3,4,5,7,8,10,11,15 |
0,1,4,5,8,10,13 |
0,1,6,8,10,13 |
|
7 |
2,3,6,7,9,11,12,13 |
0,1,2,3,9,11,12 |
0,1,6,7,9,12,13 |
|
8 |
0,2,5,6,7,8,10,15 |
5,6,7,8,9,12,15 |
5,6,7,9,11,13 |
|
9 |
2,3,5,7,10,11,12,14 |
0,2,3,4,8,10,11 |
0,5,7,8,12,14 |
|
10 |
0,2,3,4,6,8,11,13 |
0,2,3,6,11,12,14 |
0,3,4,6,9,11 |
|
11 |
2,3,4,5,12,13,14,15 |
2,3,4,5,8,9,13 |
0,4,5,8,9,11 |
|
12 |
0,1,5,10,11,12,14,15 |
4,8,10,11,12,14,15 |
0,1,8,10,12,14 |
|
13 |
0,2,3,4,5,10,12,13 |
4,5,9,10,11,12,13 |
2,3,6,10,14,15 |
|
14 |
1,4,5,6,8,9,10,11 |
1,4,5,6,8,9,12 |
1,5,8,9,12,14 |
|
15 |
1,2,3,4,10,13,14,15, |
0,2,4,10,13,14,15 |
1,2,4,10,13,15 |
|
16 |
4,5,6,7,8,9,12,15 |
0,1,2,4,8,9,12 |
0,3,4,5,6,12 |
|
17 |
0,1,4,5,10,12,14,15 |
0,1,4,5,9,12,14 |
4,5,10,12,14,15 |
|
18 |
1,2,5,6,9,10,13,14 |
0,3,4,7,11,12,15 |
0,4,11,12,13,15 |
|
19 |
1,3,4,7,8,10,12,13 |
0,1,3,4,7,9,15 |
0,5,8,10,12,13 |
|
20 |
0,2,5,6,7,8,12,13 |
0,2,4,6,8,12,13 |
0,2,4,8,12,13 |
|
21 |
0,4,7,8,11,12,14,15 |
0,3,4,7,8,12,15 |
0,3,4,5,7,12 |
|
22 |
1,3,4,6,8,11,12,14 |
0,1,4,6,8,12,14 |
0,1,3,8,9,11 |
|
23 |
1,3,5,7,9,10,12,13 |
1,3,4,5,7,8,12 |
0,2,9,10,12,13 |
|
24 |
0,2,4,7,9,11,14,15 |
0,2,5,8,9,14,15 |
4,5,7,8,9,11 |
|
25 |
0,1,5,7,9,10,13,14 |
2,3,4,6,9,12,13 |
0,5,7,9,10,14 |
|
26 |
0,1,6,7,9,11,14,15 |
2,6,7,8,10,14,15 |
2,3,4,5,9,11 |
|
27 |
1,5,7,8,10,12,13,15 |
0,1,2,5,7,13,15 |
0,2,8,10,12,13 |
|
28 |
0,2,4,5,9,11,13,15 |
0,4,5,8,9,12,13 |
0,2,4,5,12,14 |
|
29 |
1,3,4,5,8,11,12,13 |
0,2,4,5,11,12,13 |
0,2,3,11,13,15 |
|
30 |
0,2,4,6,9,10,11,12 |
0,2,4,5,8,13,15 |
2,3,6,8,9,12 |
|
СИНТЕЗ МНОГОВЫХОДНЫХ КОМБИНАЦИОННЫХ СХЕМ |
|||
|
Группа 2 |
|||
|
Вариант |
F1(x4,x3,x2,x1) |
F2(x4,x3,x2,x1) |
F3(x4,x3,x2,x1) |
|
1 |
0,1,2,5,7,13,15 |
1,5,7,8,10,12,13,15 |
0,2,8,10,12,13 |
|
2 |
0,4,5,8,9,12,13 |
0,2,4,5,9,11,13,15 |
0,2,4,5,12,14 |
|
3 |
0,2,4,5,11,12,13 |
1,3,4,5,8,11,12,13 |
0,2,3,11,13,15 |
|
4 |
0,2,4,5,8,13,15 |
0,2,4,6,9,10,11,12 |
2,3,6,8,9,12 |
|
5 |
0,2,3,6,11,12,14 |
0,2,3,4,6,8,11,13 |
0,3,4,6,9,11 |
|
6 |
2,3,4,5,8,9,13 |
2,3,4,5,12,13,14,15 |
0,4,5,8,9,11 |
|
7 |
4,8,10,11,12,14,15 |
0,1,5,10,11,12,14,15 |
0,1,8,10,12,14 |
|
8 |
4,5,9,10,11,12,13 |
0,2,3,4,5,10,12,13 |
2,3,6,10,14,15 |
|
9 |
1,4,5,6,8,9,12 |
1,4,5,6,8,9,10,11 |
1,5,8,9,12,14 |
|
10 |
0,1,4,6,8,9,15 |
0,1,2,3,6,8,9,14 |
0,2,8,9,10,15 |
|
11 |
0,3,7,8,9,12,13 |
1,2,4,5,8,12,13 |
1,4,5,8,10,11 |
|
12 |
1,3,9,11,12,13,14 |
0,1,3,4,6,9,11,14 |
0,1,8,10,12,13 |
|
13 |
2,6,7,10,11,12,14 |
0,1,6,7,8,9,12,14 |
0,1,5,6,12,14 |
|
14 |
2,4,7,8,10,12,15 |
1,3,4,7,8,12,14,15 |
2,4,8,10,12,14 |
|
15 |
0,3,4,7,8,12,15 |
0,4,7,8,11,12,14,15 |
0,3,4,5,7,12 |
|
16 |
0,1,4,6,8,12,14 |
1,3,4,6,8,11,12,14 |
0,1,3,8,9,11 |
|
17 |
1,3,4,5,7,8,12 |
1,3,5,7,9,10,12,13 |
0,2,9,10,12,13 |
|
18 |
0,2,5,8,9,14,15 |
0,2,4,7,9,11,14,15 |
4,5,7,8,9,11 |
|
19 |
2,3,4,6,9,12,13 |
0,1,5,7,9,10,13,14 |
0,5,7,9,10,14 |
|
20 |
0,2,4,10,13,14,15 |
1,2,3,4,10,13,14,15, |
1,2,4,10,13,15 |
|
21 |
0,1,2,4,8,9,12 |
4,5,6,7,8,9,12,15 |
0,3,4,5,6,12 |
|
22 |
0,1,4,5,9,12,14 |
0,1,4,5,10,12,14,15 |
4,5,10,12,14,15 |
|
23 |
0,3,4,7,11,12,15 |
1,2,5,6,9,10,13,14 |
0,4,11,12,13,15 |
|
24 |
0,1,3,4,7,9,15 |
1,3,4,7,8,10,12,13 |
0,5,8,10,12,13 |
|
25 |
0,1,4,5,8,10,13 |
3,4,5,7,8,10,11,15 |
0,1,6,8,10,13 |
|
26 |
0,1,2,3,9,11,12 |
2,3,6,7,9,11,12,13 |
0,1,6,7,9,12,13 |
|
27 |
5,6,7,8,9,12,15 |
0,2,5,6,7,8,10,15 |
5,6,7,9,11,13 |
|
28 |
0,2,3,4,8,10,11 |
2,3,5,7,10,11,12,14 |
0,5,7,8,12,14 |
|
29 |
0,2,4,6,8,12,13 |
0,2,5,6,7,8,12,13 |
0,2,4,8,12,13 |
|
30 |
2,6,7,8,10,14,15 |
0,1,6,7,9,11,14,15 |
2,3,4,5,9,11 |
Комбинационная схема с m выходами описывается системой m логических уравнений. (Для каждого выхода – свое уравнение.)
Простейший подход к синтезу таких схем – реализация каждого уравнения системы в отдельности, но получаемый результат будет далеко не лучшим. При решении задачи оптимального синтеза многовыходных схем возникает много трудностей, не преодоленных до сегодняшнего дня. Существует несколько, достаточно общих, методов синтеза многовыходных комбинационных схем. В основе всех этих способов лежит идея использования одной функции или ее части для получения других функций. Например, пусть заданы функции:
![]()
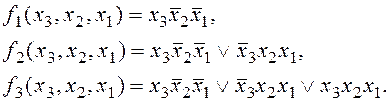
Вполне очевидно, что при синтезе можно использовать соотношения:
![]()
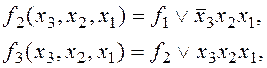
что значительно сократит объем необходимого оборудования.
Удобным и наглядным для синтеза многовыходных схем является способ с использованием карт Карно.
Применение этою способа покажем на примере.
Пусть даны три функции:
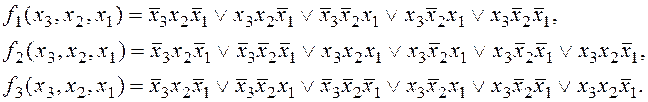
Составим для этих функций карты Карно (рис, 2.7).
|
f1 |
f2 |
f3 |
||||||||||||||||
|
x3\x2x1 |
00 |
01 |
11 |
10 |
x3\x2x1 |
00 |
01 |
11 |
10 |
x3\x2x1 |
00 |
01 |
11 |
10 |
||||
|
0 |
0 |
|
0 |
1* |
0 |
1 |
0 |
0 |
1* |
0 |
1 |
1 |
0 |
1* |
||||
|
1 |
1* |
1* |
0 |
1* |
1 |
1* |
1* |
1 |
1* |
1 |
1* |
1* |
0 |
1* |
||||
При сравнении карт легко видеть, что функции имеют четыре общих минтерма (эти минтермы отмечены звездочкой), которые можно выразить некоторой функцией
![]() .
.
С учетом этого выражения функции f1, f2, f3 можно представить следующим образом
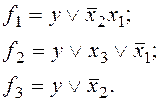
Теперь эти функции можно реализовать обычным образом (не забыв
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.