Уравнение плоскости. Уравнение прямой в пространстве. Виды уравнения плоскости. Общее уравнение плоскости, страница 4

2(3t-2)+(-t+2)+3(2t-1)-8=0

6t-4-3t+6+6t-3-8=0

9t-9=0

t=1

тогда координаты искомой точки

искомая точка пересечения имеет координаты (1;1;1).

Пример 9:

Найти уравнение плоскости проходящей через параллельные прямые.

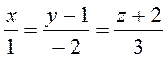
Решение:

Сделаем схематический чертёж (Рис 5.9)

 

Рис 5.9

Из заданных уравнений прямых  и  определяем проекции направляющих векторов этих прямых   . Найдём проекции вектора , лежащего в плоскости Р, а точки и берём из канонических уравнений прямых М₁ (1,-1,2) и М₂ (0,1,-2).

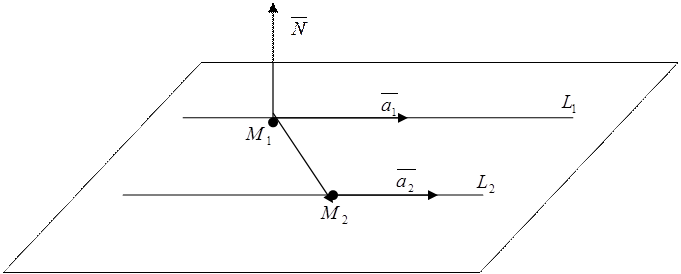Таким образом, имеем два неколлинеарных вектора  и принадлежащих искомой плоскости Р. Вектор являющийся векторным произведением этих векторов, можно взять в качестве направляющего вектора

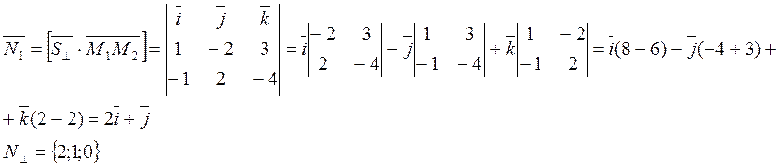Теперь у нас есть вектор перпендикулярный плоскости и точка лежащая в плоскости. Тогда искомое уравнение плоскости имеет вид:

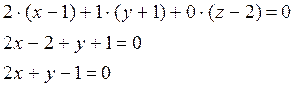
Пример 10:

Найти расстояние между двумя заданными параллельными прямыми.

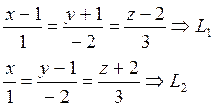
Решение:

Сделаем схематический чертёж (Рис 5.10)

 

p

M₁              S₁          L₁

M₂                      L₂

		Рис 5.10

 

Для решения этой задачи найдём уравнение вспомогательной плоскости Р перпендикулярной параллельным прямым L₁ и L₂ и проходящей через точку М₁ (1,-1,2) лежащую на прямой L₁. В качестве направляющего вектора  этой плоскости может быть взять направляющий вектор прямой L₁ . Тогда уравнение плоскости Р

1(х-1)-2(у+1)+3(z-2)=0

х-1-2у-2+3z-6=0

х-2у+3z-9=0

Найдём точку пересечения прямой L₂ и плоскости Р, для этого уравнение прямой L₂ представим в параметрическом виде:

x=t;      y=-2t+1;     z=3t-2

Находим значение параметра t соответствующее точке пересечения прямой L₂ и плоскости Р, точка М₂

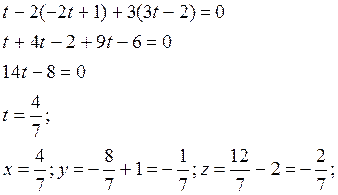
таким образом координаты точки М₂

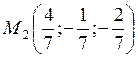
Найдём расстояние между двумя точками М₁ и М₂ это и будет расстояние между параллельными прямыми L₁ и L₂.

Задачи для самостоятельного решения

1.  Проверить проходит ли плоскость 3х-5у+2z-17=0 через точки А(4,1,2); В(2,-1,3); С(7,1,2)

2.  Найти на плоскости, заданной уравнением у+z-2=0, такую точку Р, чтобы прямая ОР составляла с осями ОY и oz углы 60⁰.

3.  Даны две точки А(-7,2,-1) и В(3,4,10). Найти уравнение плоскости проходящей через точку В перпендикулярную и отрезку АВ.

4.  Найти уравнение плоскости проходящей через ось ОХ и через точку (3,2,-7).

5.  Найти угол между плоскостями х+у-11=0 и 3х+8=0.

6.  Найти уравнение плоскости проходящей через начало координат и перпендикулярной плоскостям:  х-у+z-7=0; 3х+2у-11z+5=0.

7.  Определить расстояние от точки А(1,2,1) до плоскости х+2у+2z-10=0.

8.  Найти расстояние между параллельными плоскостями: 3х+2у-6z-56=0; 3х+2у-6z-35=0.

9.  Определить лежат ли точки А(5,-2,-3) и В(8,3,1) на прямой заданной пересечением двух плоскостей:

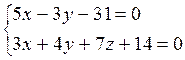
10.  Привести уравнение прямой, заданной пересечением двух плоскостей к каноническому виду:

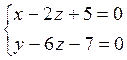
11.  Проверить лежат ли прямые в одной плоскости.

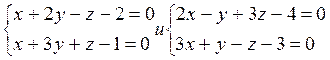
12.  Найти угол между прямой и плоскостью, если прямая задана как пересечение двух плоскостей: 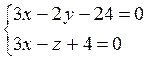, а уравнение плоскости имеет вид: 6х+15у-10z+31=0.

13.  Найти уравнение плоскости проходящей через точку      (-1,-2,-3) и параллельно прямым

14.  Составить уравнение плоскости проходящей через прямую, заданную пересечением двух плоскостей: 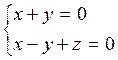 и параллельно прямой х=у=z.

15.  Решить задачу, рассмотренную в примере 11 без составления уравнения вспомогательной плоскости.