Уравнение плоскости. Уравнение прямой в пространстве. Виды уравнения плоскости. Общее уравнение плоскости, страница 2

Пусть заданы две точки М₁ (x₁,y₁,z₁) и М₂ (x₂,y₂,z₂). Уравнения прямой, проходящей через две заданные точки получаются так же, как аналогичное такое уравнение на плоскости. Поэтому сразу приведём вид этого уравнения.

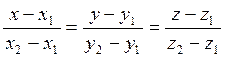
5.3.4 Прямая на пересечении двух плоскостей. Общее уравнение прямой в пространстве.

Если рассмотреть две не параллельные плоскости, то их пересечением будет прямая.

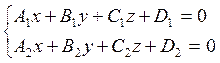
Если нормальные вектора  и  неколенеарны.

Ниже при рассмотрении примеров мы покажем способ преобразования таких уравнений прямой к каноническим уравнениям.

5.4 Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых.

Углом между двумя прямыми в пространстве будем называть любой из углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть две прямые заданны своими каноническими уравнениями.

За угол между двумя прямыми примем угол между направляющими векторами.

 и

Условие перпендикулярности двух прямых сводится к условию перпендикулярности их направляющих векторов  и , то есть к равенству нулю скалярного произведения:  или в координатной форме:  .

Условие параллельности двух прямых сводится к условию параллельности их направляющих векторов  и

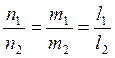
5.5 Взаимное расположение прямой и плоскости.

Пусть заданы уравнения прямой:

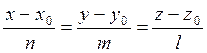
и плоскости . Углом  между прямой и плоскостью будем называть любой из двух смежных углов, образованных прямой и ее проекцией на плоскость (Рис 5.5).

 

Рис 5.5

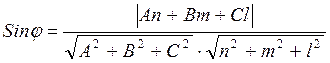
В случае перпендикулярности прямой к плоскости направляющий вектор прямой и нормальный вектор к плоскости коллинеарны. Таким образом, условие перпендикулярности прямой и плоскости сводится к условию коллинеарности векторов

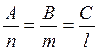
В случае параллельности прямой и плоскости их указанные выше вектора взаимно перпендикулярны. Поэтому условие параллельности прямой и плоскости сводится к условию перпендикулярности векторов ; т.е. их скалярное произведение равно нулю  или в координатной форме: .

Ниже рассмотрены примеры решения задач, связанных с темой главы 5.

Пример 1:

Составить уравнение плоскости, проходящей через точку А (1,2,4) перпендикулярную прямой, заданной уравнением:

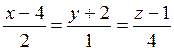
Решение:

Воспользуемся уравнением плоскости проходящей через заданную точку перпендикулярную заданному вектору.

А(х-х₀)+В(у-у₀)+С(z-z₀)=0

В качестве точки возьмём точку А (1,2,4), через которую проходит по условию плоскость.

Зная канонические уравнения прямой, мы знаем вектор, параллельный прямой .

В силу того, что по условию прямая перпендикулярна искомой плоскости, направляющий вектор может быть взят в  качестве нормального вектора плоскости.

Таким образом уравнение плоскости получим в виде:

2(х-1)+1(у-2)+4(z-4)=0

2х+у+4z-16=0

2х+у+4z-20=0

Пример 2:

Найти на плоскости 4х-7у+5z-20=0 такую точку Р, для которой ОР составляет с осями координат одинаковые углы.

Решение:

Сделаем схематический чертёж. (Рис. 5.6)

z

 

                                                          Р

0

                                                                                              у х

Рис 5.6

Пуст точка Р имеет координаты . Так как вектор  составляет одинаковые углы с осями координат, то направляющие косинусы этого вектора равны между собой

Найдём проекции вектора:

тогда легко находятся направляющие косинусы этого вектора.

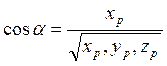
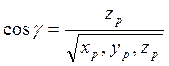
Из равенства направляющих косинусов следует равенство:

х_р=у_р=z_р

так как точка Р лежит на плоскости, то подстановка координат этой точки в уравнение плоскости обращает его в тождество.

4х_р-7х_р+5х_р-20=0

2х_р=20

х_р=10

Соответственно: у_р=10; z_р=10.

Таким образом искомая точка Р имеет координаты Р(10;10;10)

Пример 3: