Уравнение плоскости. Уравнение прямой в пространстве. Виды уравнения плоскости. Общее уравнение плоскости, страница 3

Даны две точки А (2,-1,-2) и В (8,-7,5). Найти уравнение плоскости, проходящей через точку В, перпендикулярную отрезку АВ.

Решение:

Для решения задачи воспользуемся уравнением плоскости, проходящей через заданную точку перпендикулярную заданному вектору.

А(х-х₀)+В(у-у₀)+C(z-z₀)=0

В качестве точки используем точку В (8,-7,5), а в качестве вектора, перпендикулярного плоскости вектор . Найдём проекции вектора :

тогда уравнение плоскости получим в виде:

6(х-8)-6(у+7)+7(z-5)=0

6х-48-6у-42+7z-35=0

6х-6у+7z-35=0

6х-6у+7z-125=0

Пример 4:

Найти уравнение плоскости, параллельной оси ОY и проходящей через точки К(1,-5,1) и М(3,2,-2).

Решение:

Так как плоскость параллельна оси ОY, то воспользуемся неполным уравнением плоскости.

Ax+Cz+D=0

В силу того, что точки К и М лежат на плоскости, получим два условия.

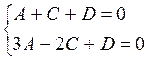
Выразим из этих условий коэффициенты А и С через D.

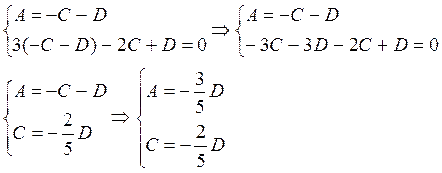
Подставим найденные коэффициенты в неполное уравнение плоскости:

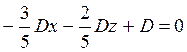
так как , то сокращаем D:

Пример5:

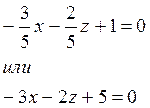
Найти уравнение плоскости проходящей через три точки М(7,6,7), К(5,10,5), R(-1,8,9)

Решение:

Воспользуемся уравнением плоскости проходящей через 3 заданные точки.

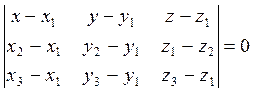
подставляя координаты точек М,К,R как первой, второй и третьей получим:

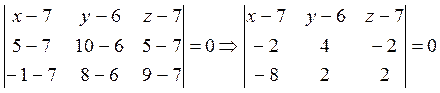
раскроем определитель по 1^ой строке.

Пример 6:

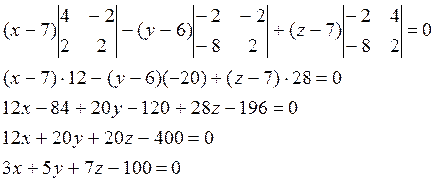
Найти уравнение плоскости, проходящей через точки М₁ (8,-3,1); М₂ (4,7,2) и перпендикулярно плоскости 3х+5у-7z-21=0

Решение:

Сделаем схематический чертёж (Рис 5.7)

 

Рис 5.7

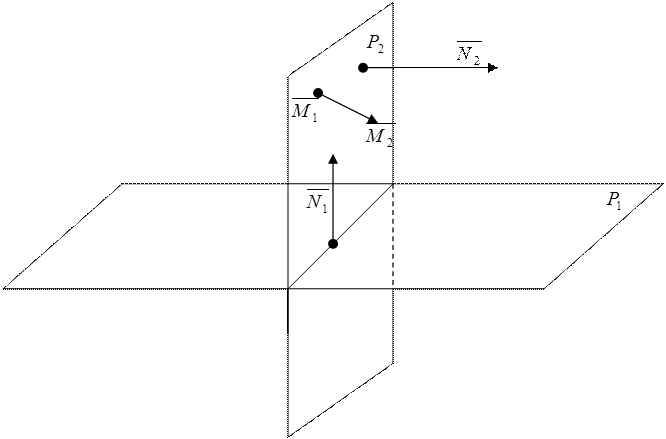Обозначим заданную плоскость Р₁ а искомую плоскость Р_2.. Из уравнения заданной плоскости Р₁ определяем проекции вектора ,   перпендикулярного плоскости Р_1.

Вектор путём параллельного переноса может быть перемещён в плоскость Р₂, так как по условию задачи плоскость Р₂ перпендикулярна плоскости Р₁ , а это значит вектор  параллелен плоскости Р_2.

Найдём проекции вектора лежащего в плоскости Р₂:

теперь мы имеем два вектора  и , лежащих в плоскости Р₂. очевидно вектор , равный векторному произведению векторов  и будет перпендикулярен плоскости Р₂, т. к. он перпендикулярен  и , поэтому его нормального вектора плоскости Р_2.

Векторы  и  заданы своими проекциями поэтому:

Далее, используем уравнение плоскости, проходящей через заданную точку перпендикулярную вектору. В качестве точки можно взять любую из точек М₁ или М₂, например М₁(8,-3,1); В качестве нормального вектора к плоскости Р₂ берём .

74(х-8)+25(у+3)+50(z-1)=0

3(х-8)+(у-3)+2(z-1)=0

3х-24+у+3+27-2=0

3х+у+2z-23=0

Пример 7:

Прямая  задана пересечением двух плоскостей. Найти канонические уравнения прямой.

 

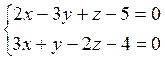
                                                              Рис 5.8

Решение:

Имеем уравнение в виде:

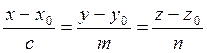
Надо найти точку (х₀,у₀,z₀), через которую проходит прямая и направляющий вектор .

Выберем произвольно одну из координат. Например,  z=1, тогда получим систему двух уравнений с двумя неизвестными:

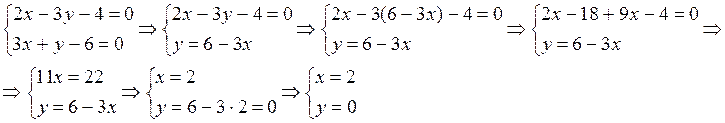
Таким образом, мы нашли точку лежащую на искомой прямой (2,0,1).

В качестве направляющего вектора  искомой прямой возьмём векторное произведения векторов  и , являющихся нормальными векторами т.к. , а значит параллельно искомой прямой.

Таким образом, направляющий вектор прямой имеет проекции . Используя уравнение прямой проходящий через заданную точку параллельно заданному вектору:

Итак искомое каноническое уравнение имеет вид:

Пример 8:

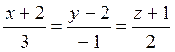Найти координаты точки пересечения прямой  и плоскости 2x+3y+3z-8=0

Решение:

Запишем заданное уравнение прямой в параметрическом виде.

х=3t-2;          y=-t+2;       z=2t-1

каждой точке прямой соответствует единственное значение параметра t. Для нахождения  параметра t соответствующего точке пересечения прямой и плоскости подставим в уравнение плоскости выражение х, у, z через параметр t.