






Определение 1: Матрицей называется прямоугольная таблица вида:
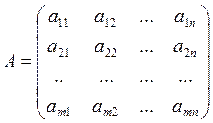
числа строк – m и число столбцов – n, называют размерами матрицы.
Определение 2: Суммой матриц А и В одинаковой
размерности ![]() называется матрица C
той же размерности
называется матрица C
той же размерности ![]() такая, что
такая, что
Сij=aij+bij для всех ij.
Определение 3: Произведением матрицы А на число ![]() называется матрица
называется матрица ![]() А элементами которой
являются
А элементами которой
являются ![]() аijдля всех i и j.
аijдля всех i и j.
Определение 4: Пусть матрица А имеет размерность ![]() , а матрица В имеет размерность
, а матрица В имеет размерность ![]() . Произведением матрицы А
и матрицы В называется матрица С=АВ размерности
. Произведением матрицы А
и матрицы В называется матрица С=АВ размерности ![]() такая, что
такая, что
Сij=ai1b1j+ai2b2j+…+ainbkj
Определение 5: Матрица называется квадратной если число ее строк равно числу столбцов.
Определение 6: Квадратная матрица вида:
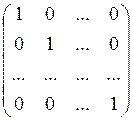
называется единичной матрицей Е.
Свойства операции умножения матриц.
1. А(ВС)=(АВ)С – ассоциативность.
2. А(В+С)=АВ+АС – дистрибутивность.
3. (А+В)С=АС+ВС - дистрибутивность.
4.
![]() - где
- где ![]() - число.
- число.
5. Если Е единичная матрица то АЕ=А и ЕВ=В.
Следует отметить, что операция умножения матриц не обладает свойством коммутативности.
![]()
6.
Любой матрице А
размером ![]() можно сопоставить матрицу АT
(матрица транспортированная к А) размером
можно сопоставить матрицу АT
(матрица транспортированная к А) размером ![]() .
Строки матрицы АT – это столбцы матрицы А с сохранением
их порядка. Причем операция умножения матриц обладает следующим свойством.
.
Строки матрицы АT – это столбцы матрицы А с сохранением
их порядка. Причем операция умножения матриц обладает следующим свойством.
![]()
Если матрица квадратичная то можно вычислить определитель такой матрицы. Причём с определителем матрицы тесно связано понятие невырожденной матрицы.
Определение 7: Квадратная матрица А называется невырожденной если ее определитель не равен нулю.
Даем еще одно очень важное свойство матриц. Оно касается обратных матриц.
Определение 8: Квадратная матрица В размерности ![]() называется обратной, если АВ=ВА=Е,
где Е – единичная матрица. Обозначается обратная матрица А-1
то есть В=А-1. Следующая теорема позволяет установить один
из способов нахождения обратных матриц.
называется обратной, если АВ=ВА=Е,
где Е – единичная матрица. Обозначается обратная матрица А-1
то есть В=А-1. Следующая теорема позволяет установить один
из способов нахождения обратных матриц.
Для всякой невырожденной квадратной матрицы А существует обратная матрица причём она вычисляется по следующему правилу.
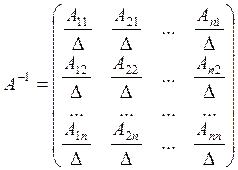
где ![]() -
определитель n- ого порядка квадратной матрицы А размерности
-
определитель n- ого порядка квадратной матрицы А размерности ![]() .
.
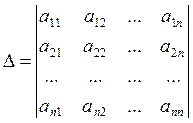
Аij – алгебраические дополнения к элементам определителя, причём следует отметить, что алгебраические дополнения вычисленные к элементам строки определителя располагаются в обратной матрице в соответствующем столбце.
Существует еще один алгоритм вычисления обратной матрицы, приведём его здесь:
1.
Приписать справа к матрице
А единичную матрицу соответствующих размеров ![]() .
.
2.
Элементарными
преобразованиями строк матрицу ![]() преобразовать
к виду
преобразовать
к виду ![]() .
.
3. Получившаяся в первой половине матрица В и будет обратной для матрицы А то есть В=А-1.
Ниже будет рассмотрен пример применения этого алгоритма.
Рассмотрим примеры решения задач по теме главы 6.
Найти матрицу С, являющуюся суммой двух матриц А и В.
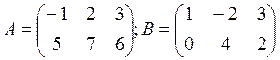
Решение:
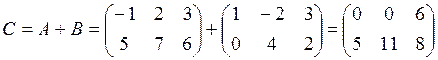 .
.
Пример 2:
Найти произведение матрицы А на число ![]() , если:
, если:
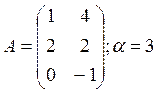
Решение:
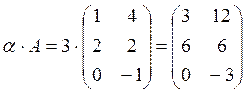 .
.
Пример 3:
Некоторая фирма занимается реализацией товара в трёх
районах. Данные об уровне продаж товаров по районам образуют матрицу А
размерности ![]() ,строки матрицы соответствуют
районам, а столбцы – видам товара. Цены на реализуемые товары образуют матрицу С
столбец размерности
,строки матрицы соответствуют
районам, а столбцы – видам товара. Цены на реализуемые товары образуют матрицу С
столбец размерности ![]() .
.
Найти матрицу Р характеризующую суммарную продажу по районам, если :
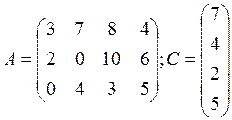
Объемы продаж заданы в тыс. штук. Цены в тыс.руб/тыс.штук.
Для нахождения матрицы Р, необходимо матрицу А
размером ![]() умножить на матрицу С
размером
умножить на матрицу С
размером ![]() . Проверяем соответствие
размерностей перемножаемых матриц, количество столбцов матрицы А равно
количеству строк матрицы. Такие матрицы можно перемножать. Размерность
результирующей матрицы Р получится
. Проверяем соответствие
размерностей перемножаемых матриц, количество столбцов матрицы А равно
количеству строк матрицы. Такие матрицы можно перемножать. Размерность
результирующей матрицы Р получится ![]() .
.
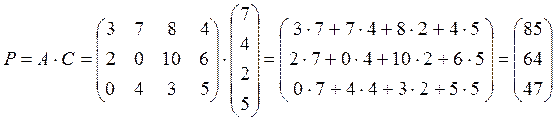
Таким образом искомая матрица Р характеризующая суммарную продажу по районам имеет вид:
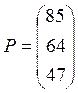 .
.
Пример 4:
Даны две матрицы А размерности ![]() и
В размерности
и
В размерности ![]() . Найти произведение
матриц А.В и В.А если:
. Найти произведение
матриц А.В и В.А если:
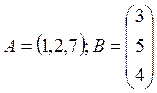
Решение:
Найдём произведение матриц А.В. Проверяя
соответствие размерностей матрицы А ![]() и
матрицы В
и
матрицы В![]() мы выделим, что
перемножение матриц возможно, причём в результате мы получаем матрицу размером
мы выделим, что
перемножение матриц возможно, причём в результате мы получаем матрицу размером ![]() , то есть матрицу, содержащую
только один элемент.
, то есть матрицу, содержащую
только один элемент.
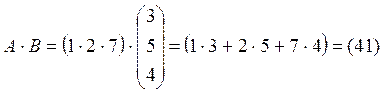
Теперь найдём произведение матриц В.А.
Произведение таких матриц тоже возможно, так как размерность матрицы В ![]() , а матрицы А
, а матрицы А ![]() , причем результирующая матрица
имеет размерность
, причем результирующая матрица
имеет размерность ![]()
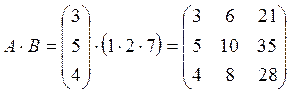
Пример 5:
Найти обратную матрицу для заданной матрицы С если:
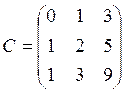
Решение:
1й способ:
Прежде чем находить С-1 определим, является ли матрица С невырожденной. Для этого найдём определитель матрицы С.
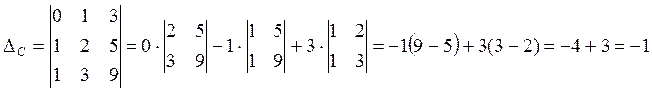
![]() матрица
является невырожденной поэтому существует обратная матрица С-1.
матрица
является невырожденной поэтому существует обратная матрица С-1.
Для того чтобы воспользоваться теоремой о нахождении обратной матрицы найдём алгебраические дополнения ко всем элементам определителя.
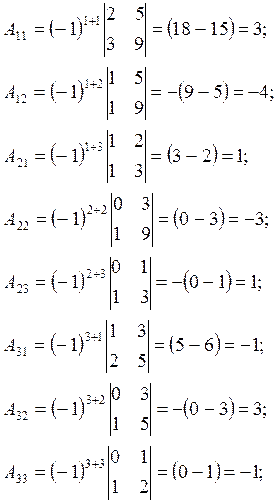
Зная алгебраические дополнения и определитель матрицы запишем обратную матрицу С-1.
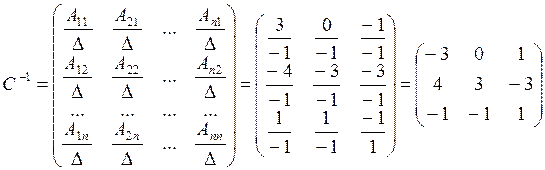
Правильность вычислений легко можно проверить
если найти произведение матриц ![]() должна
получится единичная матрица Е.
должна
получится единичная матрица Е.
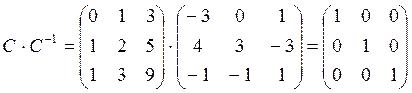
таким образом вычисления проведены верно.
2й способ:
Найдём обратную матрицу с помощью алгоритма нахождения обратной матрицы.
Задана матрица С
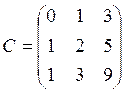
припишем справа единичную матрицу Е
размером ![]() получим:
получим:
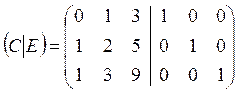
осуществляем элементарные преобразования строк, чтобы преобразовать матрицу к виду
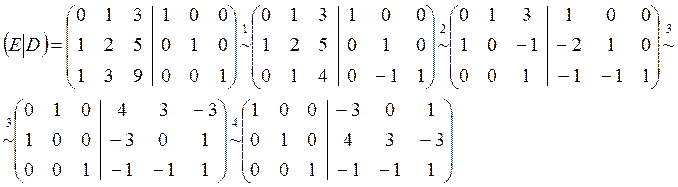
Полученная матрица D является обратной к матрице С, то есть:
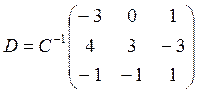
В процессе преобразования матрицы были выполнены следующие элементарные преобразования:
1. Из третьей строки вычли вторую строку и результат записали на место третьей строки.
2. а) Первую строку умножили на (-2) и сложили со второй строкой, результат записали на место второй строки.
б) Первую строку умножили на (-1) и сложили с третьей строкой, результат записали на место третьей строки.
3. а) Третью строку сложили со второй строкой, результат записали на место второй строки.
б) Третью строку умножили на (-3) и сложили с первой строкой, результат записали на место первой строки.
4. Поменяли местами первый и второй столбцы.
Задачи для самостоятельного решения
1. Найти произведение матриц АВ и ВА если заданы матрицы А и В.
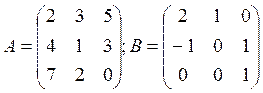
2. Найти сумму матриц А и В если:
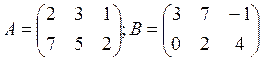
3.
Предприятие выпускает три
вида продукции П1,П2,П3 используя два вида
сырья S1,
S2.
нормы расхода сырья заданы матрицей А размером ![]() . Где столбцы характеризуют виды
продукции, а строки виды сырья. План выпуска продукции задан матрицей столбцом С
размером
. Где столбцы характеризуют виды
продукции, а строки виды сырья. План выпуска продукции задан матрицей столбцом С
размером ![]() . Стоимость каждого из видов
сырья в расчёте на единицу сырья заданы матрицей строкой Р размером
. Стоимость каждого из видов
сырья в расчёте на единицу сырья заданы матрицей строкой Р размером ![]() . Найти реализации данного плана
если:
. Найти реализации данного плана
если:
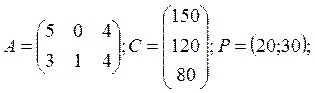
4.
Для матрицы 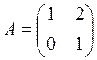 вычислить матрицы А2=А.А;
А3=А2.А;
В=Е-2А+А2, где Е единичная матрица.
вычислить матрицы А2=А.А;
А3=А2.А;
В=Е-2А+А2, где Е единичная матрица.
5. При каком соотношении между параметрами k и l будет справедливо равенство АВ=ВА если:
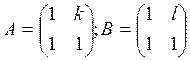
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.