



В этом приложении приведём разбор аудиторной контрольной работы, которая даётся студентам первого курса и является обязательным контрольным мероприятием. Контрольная состоит из 5 задач.
Задача1:
Решить неравенство
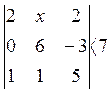
Решение:
Вычислим определитель третьего порядка раскрываем его по первой строке.
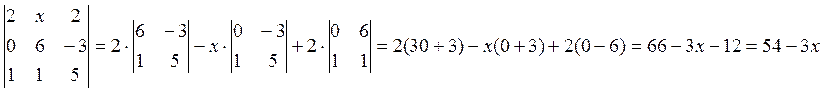 тогда неравенство преобразуется
к виду
тогда неравенство преобразуется
к виду
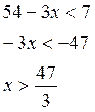
Ответ: 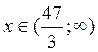
а) угол между векторами ![]() и
и![]()
б) площадь треугольника АВС
с) Объём пирамиды АВСD.
Решение:
а) Для
нахождения угла между векторами ![]() и
и ![]() найдём проекции этих векторов
найдём проекции этих векторов
![]() ;
; ![]()
Далее используем формулу нахождения угла между векторами заданными
своими проекциями. Обозначим искомый угол ![]() .
.
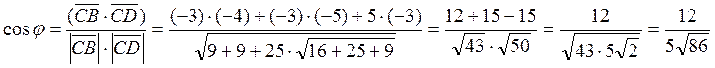
Зная 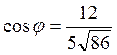 по таблицам
находим угол
по таблицам
находим угол ![]() .
.
б) Для нахождения площади треугольника АВС найдём проекции
векторов ![]() и
и ![]()
![]()
Известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах.
Тогда площадь треугольника АВС будет равна половине площади параллелограмма. Таким образом.
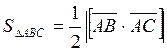
Найдём векторное произведение векторов ![]() и
и ![]() заданных
своими проекциями
заданных
своими проекциями
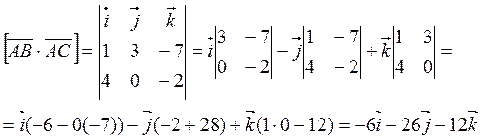
Таким образом, проекции вектора векторного произведения будут: (-6: -26: -12)
Тогда легко находим модуль векторного произведения:
![]()
Отсюда: 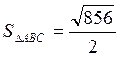 ед. кв.
ед. кв.
в) Для нахождения объёма пирамиды АВСD необходимо знать проекции векторов ![]()
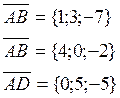
из векторной алгебры известно, что объем пирамиды может быть вычислен с помощью смешанного произведения векторов образующих пирамиду
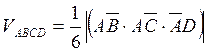
Найдём смешанное произведение векторов заданных своими проекциями
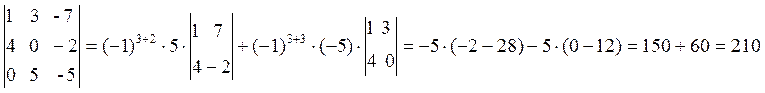
тогда искомый объем пирамиды
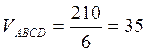 куб. ед.
куб. ед.Найти вектор![]() , если
известно, что
, если
известно, что ![]()
причем проекции векторов ![]() заданы:
заданы:
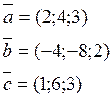
Решение:
Обозначим проекции вектора ![]() тремя
неизвестными х, у, z, то есть
тремя
неизвестными х, у, z, то есть ![]()
Зная проекции векторов ![]() запишем
скалярное произведение векторов заданных своими проекциями.
запишем
скалярное произведение векторов заданных своими проекциями.
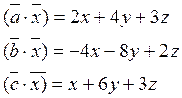
используя заданные начальные условия, получим систему с тремя неизвестными:
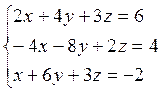
Решая эту систему, получаем:
x=4; у=-2; z=2;
таким образом, искомый вектор ![]() имеет
проекции:
имеет
проекции:
![]()
Даны две вершины треугольника А(-6;2) В(2;-2) и точка Н(1;2) пересечения его высот. Вычислить координаты третьей вершины С.
|
|
|
|
|
|
Найдём уравнение стороны треугольника АС используя уравнение прямой проходящей через заданную точку перпендикулярно заданному вектору: А(х-х0)+В(у-у0)=0.
В качестве вектора перпендикулярного АС возьмем вектор ![]() , лежащий на высоте
треугольника, проведённая из вершины В к стороне АС
, лежащий на высоте
треугольника, проведённая из вершины В к стороне АС
![]()
В качестве точки, через которую проходит прямая координаты точки А, тогда имеем уравнение АС.
-1(х+6)+4(у-2)=0
-х-6+4у-8=0
-х+4у-14=0
х-4у+14=0
Аналогично найдём уравнение стороны треугольника ВС. Вектор
перпендикулярный к ВС вектор ![]() :
:
![]() (7;0)
(7;0)
Точка, через которую проходит ВС – точка В (2;-2)
7(х-2)+0(у+2)=0
7х-14=0
х-2=0
Имеем уравнения двух прямых, которые пересекаются в точке С. Для нахождения координат точки С решим систему уравнений
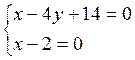
таким образом некоторые координаты С(2;4)
Вычислить расстояние между параллельными плоскостями заданными уравнениями
x-2у+3z=0 и х-2у+3z-5=0
Обозначим Р1 плоскость х-2у+3z=0, а Р2 плоскость х-2у+3z-5=0.
Найдём точку припадающую плоскости Р1. Для этого положим две координаты х=0 и у=0, тогда имеем 0-2*0+3z=0 => z=0. То есть плоскость Р1 проходит через начало координат, таким образом точка (0,0,0) принадлежит плоскости Р1. Найдём расстояние от этой точки до плоскости Р2 . Это и будет искомое расстояние между параллельными плоскостями Р1 и Р2. Для этого воспользуемся формулой расстояния от заданной точки до заданной плоскости:
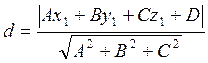
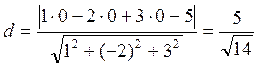
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.