Расчёт статически-неопределимых систем методом сил. Общие понятия о статически-неопределимых системах, страница 3

Для решения уравнений (6.5.) можно воспользоваться различными математическими методами (например, метод Гаусса) или готовыми компьютерными программами для решения систем  линейных уравнений.

7.4. Техника вычисления коэффициентов канонических уравнений

В предыдущей лекции было показано, что для вычисления перемещений удобно пользоваться правилом Верещагина. Для этой цели от нагрузки, а также от всех единичных значений неизвестных рекомендуется построить эпюры моментов, продольных и поперечных сил. Для систем рамного типа, элементы которых в основном работают на изгиб, учитывается, как правило, только один член формулы Мора, зависящий от моментов, поэтому обычно строятся только эпюры моментов. 

Рассмотрим технику вычислений коэффициентов канонических уравнений на примере. На рис. 6.5. а  показана трижды статически неопределимая рама с равномерно распределенной нагрузкой на горизонтальном элементе q = 2Кн/м. Основная система изображена на рис. 6.5. б. Отметим, что заранее нельзя предугадать направление действия реакций. Однако в этом нет необходимости, так как направления действия неизвестных можно принимать произвольно. В случае ошибки коррективу внесут окончательные результаты вычислений. Если некоторые из неизвестных окажутся отрицательными, то это означает, что их истинные направления противоположны принятым в начале расчета.

В рассматриваемой раме стойки имеют жесткость EI, а горизонтальный стержень -  2EI  . Как увидим в последующем, абсолютное значение жесткости задавать нет необходимости, так как оно войдет во все коэффициенты уравнений и затем сократится.  

Эпюра моментов в основной системе от нагрузки  M_P  и три эпюры от единичных неизвестных  M₁ , M₂  и M₃  показаны на рис. 6.6. Все ординаты эпюр отложены со стороны растянутого волокна.

 

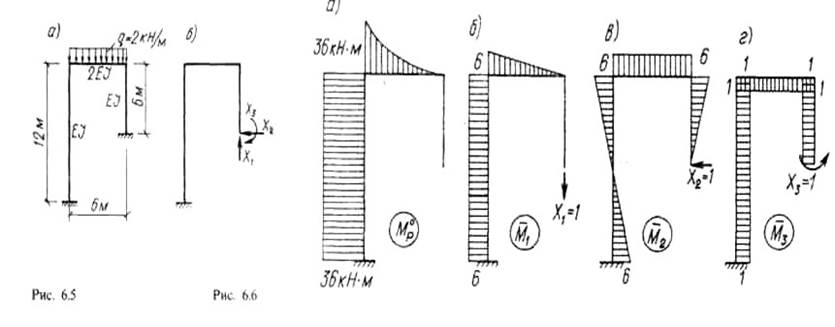
Пользуясь правилом Верещагина, по которому интегралы Мора находятся путем перемножения эпюр, найдем все необходимые коэффициенты канонических уравнений. Термин «перемножение» эпюр (или «сопряжения» эпюр) является условным. Напомним, что по правилу Верещагина каждый из интегралов Мора подсчитывается умножением площади одной эпюры на ординату другой эпюры. Ордината второй эпюры берется в месте расположения центра тяжести площади первой эпюры. Вначале вычислим главные перемещения от единичных неизвестных:

       d₁₁ = MEI₁²ds = 6EI12( )6 + 12 (26EI6)Ł 32 6ł+ 0 = 468EI                                            

                             M22ds = 2Ø1 6 6     2    ø

d22 =        EI  Œº2 (2EI)Ł 36łœß+ 26EI6 ( )6 + 12 (26EI6)Ł 326ł= 324EI

       d₃₃ = MEI₃²ds = 1EI12( )1 + (₂1_EI6 )( )1 + (1_EI6)( )1 = _EI21

Вычислим побочные перемещения от единичных неизвестных:

            d12 =d21 = M1EIM2ds = 0+ 12 (26EI6)( )6 + 0 = EI54

            d13 =d31 = M₁EIM₃ds =- 6EI12( )1 - 12 (₂6_EI6)( )1 + 0 =- _EI81

            d23 =d32 =   M₂EIM₃ds = 0 - 26EI6 ( )1 - 12 (6_EI6)( )1 = - _EI36

Теперь найдем перемещения от нагрузки (площади берутся в эпюре  M_P )

D1P =	M1 MPds = 36 12( )6 + 1 (362EI6)Ł 436ł+ 0 = 2754EI ;          EI               EI            3
D2P =	M2 MPds = 0 + 1 (36 6)( )6 + 0 = 216 ;

                                                     EI                   3 2EI                  EI

            D3P =   M₃ M_Pds = - 36 12( )1 - 1 (36 6)( )1 + 0 =- 468 .

                                                     EI                  EI            3 2EI                    EI

            Дадим некоторые пояснения к проведенным вычислениям:

1)  каждое из перемещений состоит из трех слагаемых: первое слагаемое     относится к левой стойке, второе - к горизонтальному элементу, третье -     к правой стойке;

2)  ординаты в местах расположения центров тяжести взяты в круглые скобки;

3)  знаки минус в выражениях d₁₃, d₂₃ и D_зр приняты потому, что сопрягаемые эпюры отложены в разные стороны.

Подставим полученные результаты в систему канонических уравнений и получим 

                    468Х₁ +54Х₂ – 81Х₃ + 2754 = 0

            54Х₁ + 324Х₂ – 36Х₃ + 216  = 0

                 - 81Х₁ - 36Х₂ + 21Х₃ – 468  = 0

Решив эту систему уравнений любым известным вам способом, получаем значения неизвестных Х₁ = -5,92562,  Х₂ = 0,31818,   Х₃ = -0,02479. 

Вычисления показали, что одно лишнее неизвестное Х₂ является положительным числом, а два других Х₁ и Х₃   оказались отрицательными. Это свидетельствует о том, что назначенное в основной системе направление Х₂ совпало с истинным направлением, а два других неизвестных в действительности направлены в противоположную сторону.

          Таким образом, при выборе основной системы можно принимать произвольное направление лишних неизвестных. В конце расчета будет выявлено их действительное направление.