Расчёт статически-неопределимых систем методом сил. Общие понятия о статически-неопределимых системах

Лекция 7

Расчёт статически-неопределимых систем методом сил

7.1. Общие понятия о статически-неопределимых системах.

В предыдущих лекциях рассматривались методы расчета статически определимых систем, в которых опорные реакции и все внутренние силовые факторы определялись с помощью только уравнений равновесия или выполнялись расчёты с помощью таблиц. На практике встречаются системы, расчет которых нельзя осуществить с помощью одних уравнений статики. Приходится составлять дополнительные уравнения, учитывающие некоторые особенности деформации системы.

Проведем анализ изгиба балки на трех опорах, расположенных в точках а, b и с (рис. 6.1). Первая опора в точке а шарнирно-неподвижная, а две другие опоры в точках b и с шарнирно-подвижные. Число опорных реакций, возникающих от произвольной нагрузки, равно четырем, а независимых уравнений статики, которые можно составить для данной системы, равно трем. Таким образом, число неизвестных превышает число уравнений статики.

Такие системы, в которых число неизвестных превышает число независимых уравнений статики, называются статически неопределимыми. Поясним вначале понятие «независимые» уравнения статики. Из теоретической механики известно, что для системы, находящейся в равновесии, сумма моментов  всех  сил относительно  любой точки равна нулю. Если для данной системы выбрать п точек (k₁, k₂, ... ,k_n) и для каждой из них составить уравнение моментов SМ _ki = 0 (i = 1, 2, ..., n), то получим п уравнений, из которых только три будут независимыми, а все остальные будут являться какой-либо комбинацией этих трех уравнений (например, сумма двух уравнений совпадает с одним из основных уравнений).

В рассматриваемом примере (см. рис. 6.1) число неизвестных реакций (H, A, В и С) на единицу превышает число уравнений статики, поэтому система называется однажды статически неопределимой. Наряду с такими системами имеются дважды, трижды и nраз статически неопределимые системы. Число п называется степенью статической неопределимости системы.

Отбросим в рассматриваемой балке одну из опор (например, среднюю), а ее реакцию заменим пока неизвестной некоторой силой X(рис. 6.2). Превратив реакцию во внешнюю силу X, вместо двух пролетной балки получим простую (однопролетную) балку. Сила оказалась как бы лишней по отношению к числу возможных уравнений статики; ее принято называть лишним неизвестным. В общем случае число лишних неизвестных совпадает со степенью статической неопределимости.

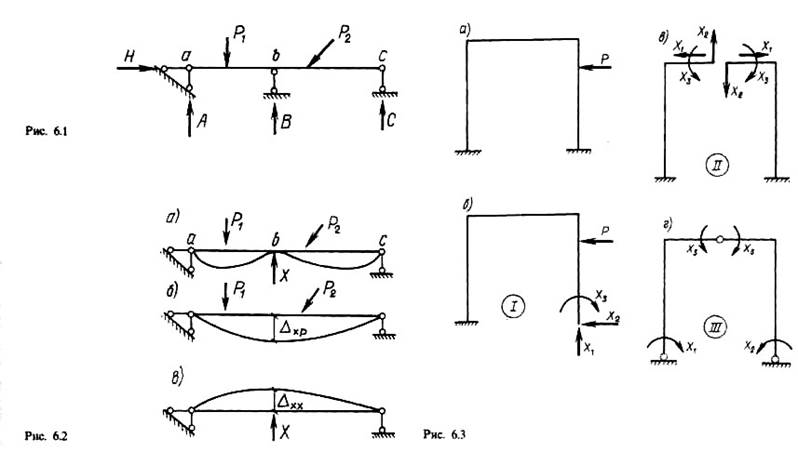
Так как в заданной системе прогиб балки над средней опорой равен нулю, то сумма перемещений этой точки от сил Р и от силы X будет равна нулю, поэтому условием для определения величины силы будет служить уравнение

                                               D_xx + D_xP = 0

Предположим, что Х=1, тогда перемещение по направлению единичной силы в соответствии с обозначениями, принятыми в гл. 5, будет d_xx , а перемещение от силы Х будет отличаться от  d_xx  во столько раз, во сколько Х отличается от единицы, поэтому D_хх = d_xx Х . Подставляя это значение в уравнение

(6.1.), получим

                                      d_xxX +D_xP = 0

Определив перемещения  d_xx и D_хР по формуле Мора (5.24.), найдем из (6.2.) значение лишнего неизвестного.

Теперь задача решается просто. Необходимо вместо средней опоры приложить найденную силу Х и рассматривать ее как внешнюю нагрузку. Вместе с заданной нагрузкой получится система внешних сил, действующих на простую балку. Расчет на действие полученной внешней нагрузки затруднений не вызывает.

            7.2. Понятие об основной системе

Основной системой называется статически определимая и геометрически неизменяемая расчётная схема, полученная из заданной. Путём отбрасывания «лишних» неизвестных. Такими «лишними» неизвестными могут быть как усилия в опорных закреплениях, шарнирных соединениях, так и внутренние усилия в сечениях. На рис. 6.3., а показана рама с двумя заделанными стойками, к которой приложена сила Р. Требуется установить степень статической неопределимости рамы и выбрать основную систему. Для этой цели необходимо путем отбрасывания связей превратить заданную систему в простую статически определимую систему. Можно составить несколько вариантов основной системы. На рис. 6.3. б, показана система, которая получена из заданной рамы путем отбрасывания заделки у правой стойки. Полученная статически определимая система представляет собой ломаный стержень, заделанный на левом конце. Вместо заделки на правом конце приложены три внутренних силовых фактора: Х₁ (продольная сила), Х₂ (поперечная сила) и Х₃ (изгибающий момент), которые являются лишними неизвестными, поэтому сама заданная система трижды статически неопределима.