ЛЕКЦИЯ 6
ПРЕДЕЛЬНЫЕ СОСТОЯНИЯ И РАСЧЕТ КОНСТРУКЦИЙ
Предельное состояние и расчет растянутых элементов
Работа центрально-растянутого элемента наглядно характеризуется диаграммой растяжения стального стандартного образца (рис. 2.1). Предельное состояние первой группы для элементов, испытывающих осевое растяжение, проверяется расчетом на прочность:
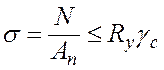 , (6.1)
, (6.1)
где N - осевое
усилие, возникающее от расчетных нагрузок; Аn - площадь сечения
с учетом ослабления; Ry - расчетное сопротивление,
установленное по пределу текучести; ![]() - коэффициент
условия работы.
- коэффициент
условия работы.
Если мы имеем дело со сталями, у которых значение
предела прочности ![]() намного больше предела
текучести
намного больше предела
текучести ![]() , а значит, имеется протяженная область
упругопластической работы (участок «в – г», рис. 2.1), целесообразно
использовать эту область работы стали, допуская развитие напряжений, превышающих
предел текучести. Исходя из этого при выполнении условия
, а значит, имеется протяженная область
упругопластической работы (участок «в – г», рис. 2.1), целесообразно
использовать эту область работы стали, допуская развитие напряжений, превышающих
предел текучести. Исходя из этого при выполнении условия ![]() , где Ru -
расчетное сопротивление, установленное по пределу прочности;
, где Ru -
расчетное сопротивление, установленное по пределу прочности; ![]() - коэффициент надежности,
принимаемый 1,3, нормы проектирования разрешают эксплуатацию растянутых
элементов после достижения металлом предела текучести (работа в упругопластической
области) и рекомендуют рассчитывать их по формуле
- коэффициент надежности,
принимаемый 1,3, нормы проектирования разрешают эксплуатацию растянутых
элементов после достижения металлом предела текучести (работа в упругопластической
области) и рекомендуют рассчитывать их по формуле
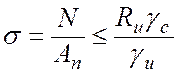 . (6.2)
. (6.2)
1. Расчет при работе в упругой стадии.
Если по условиям работы изгибаемого элемента допускается только упругая стадия, за предельное состояние принимается момент достижения максимальными напряжениями значений предела текучести.
Прочность таких элементов при изгибе в одной плоскости проверяется по формуле:
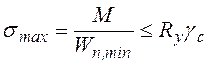 , (6.3)
, (6.3)
где М - изгибающий момент, вычисленный
по расчетным нагрузкам; ![]() - минимальный
момент сопротивления сечения с учетом ослабления.
- минимальный
момент сопротивления сечения с учетом ослабления.
Прочность изгибаемых элементов в месте действия максимальной перерезывающей силы проверяется по формуле:
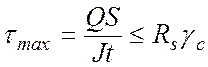 , (6.4)
, (6.4)
где Q - перерезывающая сила, вычисленная по расчетным нагрузкам; S - статический момент сдвигающейся части сечения относительно нейтральной оси; J - момент инерции сечения элемента; t - ширина сечения в месте действия максимальных касательных напряжений; Rs - расчетное сопротивление стали срезу, Rs = 0,58Rу.
Если в одном и том же сечении одновременно действуют изгибающий момент и поперечная сила, прочность изгибаемого элемента в этом сечении проверяется по формуле:
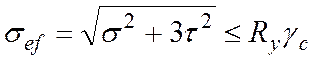 , (6.5)
, (6.5)
где ![]() - приведенное
напряжение (см. лекцию 4);
- приведенное
напряжение (см. лекцию 4); ![]() и
и ![]() - соответственно нормальное и
касательное напряжение, вычисленные для наиболее опасного места сечения.
- соответственно нормальное и
касательное напряжение, вычисленные для наиболее опасного места сечения.
2. Расчет при работе в упругопластической стадии.
Рис. 6.1. Образование шарнира пластичности при изгибе:
а – эпюры нормальных напряжений в упругой стадии работы материала;
б – то же, в упругопластической стадии; в – эпюра напряжений,
соответствующая образованию шарнира пластичности
После исчерпания упругой работы (рис. 6.1, а) в элементах из пластичных сталей пластические деформации начинают распространяться в глубь сечения (рис. 6.1, б) и в предельном состоянии пронизывают все сечение
(рис. 6.1, в).
Образуется так называемый шарнир пластичности. В сечении с шарниром
пластичности все фибры находятся в стадии текучести (верхняя часть сечения
равномерно сжата напряжениями, равными ![]() ,
нижняя - растянута), что выражается в нарастании деформаций, в результате
которых балка получает угол перелома и поворачивается вокруг нейтральной оси сечения
как вокруг оси шарнира. Однако в отличие от обычного шарнира момент в пластическом
шарнире не равен нулю, а поворот возможен лишь в одном направлении.
,
нижняя - растянута), что выражается в нарастании деформаций, в результате
которых балка получает угол перелома и поворачивается вокруг нейтральной оси сечения
как вокруг оси шарнира. Однако в отличие от обычного шарнира момент в пластическом
шарнире не равен нулю, а поворот возможен лишь в одном направлении.
Очевидно, что после появления в сечении балки шарнира пластичности дальнейшая эксплуатация ее не представляется возможной, а эпюра (рис. 6.1, в) соответствует предельному состоянию при работе балки в упруго-пластической стадии.
Величина момента внутренних сил в сечении с шарниром пластичности определяется из выражения
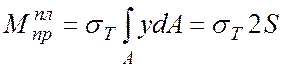 , (6.6)
, (6.6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.