Предельные состояния и расчет конструкций. Предельное состояние и расчет растянутых элементов. Образование шарнира пластичности при изгибе, страница 2

где dA - бесконечно малая площадь сечения; у - ее ордината; A - полная площадь сечения; S - статический момент половины сечения относительно нейтральной оси.

Выразим значение предельного момента, ограничивающего упругую работу изгибаемого элемента (эпюра «а» на рис. 6.1).

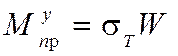                                       .                                                (6.7)

Приведем к такому же виду предельный момент, отвечающий шарниру пластичности,

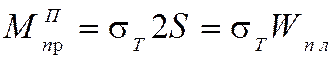                                       .                       (6.8)

Здесь 2S играет роль пластического момента сопротивления  .

Пластический момент сопротивления больше упругого. Например, для прямоугольного сечения ; для двутавров при изгибе в плоскости стенки  и т.д.

В общем виде можно записать: , где c> 1.

Как уже отмечалось, при образовании шарнира пластичности в сечении элемента происходит неограниченный (если не учитывать работу материала в стадии самоупрочнения) рост пластических деформаций и нарастание прогиба балки. Однако исчерпание несущей способности конструкции наступает еще раньше, так как, если разгрузить балку до образования шарнира пластичности, остаточные деформации ее оказываются столь большими, что конструкция становится непригодной к дальнейшей эксплуатации, т.е. имеет место предельное состояние первой группы.

В качестве критерия предельного состояния по непригодности к эксплуатации принята ограниченная пластическая деформация в сечении. Нормы проектирования для практических расчетов предусматривают предельную относительную пластическую деформацию

                                       _ост=_ост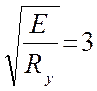.                                           (6.9)

Поэтому расчет изгибаемых элементов с учетом развития пластических деформаций выполняется по расчетному пластическому моменту сопротивления, величина которого определяется по формуле

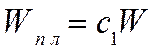                                       ,                                                   (6.10)

где с₁ вычисляется из условия _ост= 3, значение с₁ всегда меньше с.

Учет пластической работы стали допускается в балках сплошного сечения,  несущих статическую нагрузку, а также при выполнении других условий, оговоренных в нормах проектирования. Проверка прочности таких балок выполняется по формуле

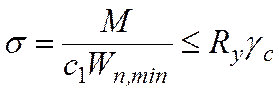                                       .                               (6.11)

При совместном действии  и  условия образования шарнира пластичности таковы, что предельная несущая способность примерно на 15 % выше, чем при упругой работе. Прочность балки в сечении, где действуют и момент, и поперечная сила, проверяется по формуле

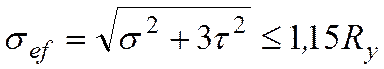                                       .              (6.12)

3. Проверка общей устойчивости балки.

Потеря несущей способности балки может произойти из-за потери устойчивости. Под нагрузкой, действующей в плоскости главной оси, балка сначала изгибается в своей плоскости, а затем, при достижении нагрузкой критического значения, начинает закручиваться и выходить из плоскости изгиба. Наступает потеря общей устойчивости балки (рис. 6.2).

Рис. 6.2. Общая потеря устойчивости двутавровой балки

Напряжения в сечении балки в момент потери устойчивости называются критическими. Величина их зависит от положения нагрузки на балке: нагрузка, приложенная к верхнему поясу балки, увеличивает скручивание, расположенная по нижнему поясу - уменьшает его, поэтому расположение нагрузки по верхнему поясу значительно опаснее.

Проверка общей устойчивости сводится к сравнению возникающих напряжений  с критическими значениями .

Наибольшие краевые напряжения в сжатом поясе балки

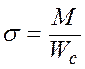                                                 ,                                                      (6.13)

где  - момент сопротивления для краевого сжатого волокна сечения балки.

Критические напряжения потери устойчивости балки

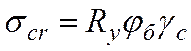                                                 ,                                    (6.14)

- коэффициент, понижающий расчетное сопротивление до значений критических напряжений потери устойчивости. Величина  зависит от типа сечения балки и места приложения нагрузки и определяется по таблицам, приведенным в нормах проектирования.

Таким образом, проверку общей устойчивости балки можно записать:

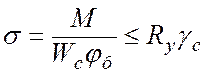                                                 .                                  (6.15)

4. Проверка упругих деформаций балки (расчет по второй группе предельных состояний)