Расчёт и конструирование сборной ребристой плиты перекрытия. Расчет прочности нормальных сечений. Расчёт прогиба панели

Министерство образования и науки РФ

Федеральное агентство по образованию

Дальневосточный Государственный Технологический Университет

( ДВПИ им. В.В. Куйбышева )

Строительный институт

Кафедра строительных конструкций и материалов

Пояснительная записка к курсовому проекту по курсу:

Железобетонные конструкции

Выполнил: студент

Гр. С-2932

Проверил: преподаватель

Владивосток 2005г.

Содержание:

1.    Расчёт и конструирование сборной ребристой плиты перекрытия. - 3 1.1       Определение нагрузок на перекрытие. - 3 1.2       Определение усилий в сечении панели перекрытия. - 4 1.3       Расчет прочности нормальных сечений. - 6 1.4       Расчет прочности наклонных сечений. - 7 1.5       Расчет  полки  плиты на местный изгиб. - 8 1.6       Расчеты плиты по 2-ой группе предельных состояний. - 9 1.6.1        Определение геометрических характеристик приведённого сечения. - 9 1.6.2        Определение потерь предварительного напряжения в арматуре. - 10 1.6.3        Расчёт на образование нормальных трещин. - 12 1.6.4        Расчёт прогиба панели. - 12 -

2.    Проектирование ригеля. - 14 2.1       Сбор нагрузок и определение усилий в сечении ригеля. - 14 2.2       Расчет прочности нормальных сечений. - 16 2.3       Расчёт прочности наклонных сечений. - 17 -

3.    Проектирование колонны подвала. - 19 3.1       Определение усилий в колонне подвала у обреза фундамента. - 19 3.2       Расчёт прочности нормальных сечений. - 20 3.3.      Проектирование консоли колонны. - 22 3.4.      Расчет стыка колонн. - 23 -

4.    Проектирование фундамента под колонну. - 25 4.1.      Определение размеров подошвы в плане. - 25 4.2       Проверка высоты фундамента из расчёта на продавливание. - 25 4.4       Расчёт арматуры у подошвы фундамента. - 26 -

5.    Расчет и конструирование монолитное ребристого перекрытия. - 28 5.1.      Компоновка перекрытия. - 28 5.2.      Расчет плиты перекрытия. - 28 5.2.1.       Расчетная схема, пролет, усилия. - 28 5.2.2.       Подбор арматуры плиты. - 29 5.3.      Расчет второстепенной балки. - 30 5.3.1.       Расчетная схема, пролет, усилия. - 30 5.3.2.       Расчет прочности нормальных сечений. - 31 5.3.3.       Расчет прочности наклонных сечений. - 33 -

Список использованной литературы. - 35 -

Приложение. - 36 -

1.     Расчёт и конструирование сборной ребристой плиты перекрытия

Исходные данные

Материалы панели:

бетон:

класс – В30;

расчетное сопротивление осевому сжатию R_b=17 МПа;

расчетное сопротивление осевому растяжению R_bt=1,2 МПа;

модуль упругости бетона E_b=32,5·10³ МПа;

коэффициент условий работы бетона γ_b2=0,9

арматура:

в продольных ребрах используется предварительно напряженная арматура класса А-ΙV

расчетное сопротивление растяжению арматуры R_s=510 МПа;

нормативное сопротивление R_sn=590 МПа;

модуль упругости стали арматуры E_s=190·10³ МПа;

1.1     Определение нагрузок на перекрытие

Вид нагрузки	Нормативная нагрузка, кН/м2	Коэффициент надёжности по нагрузке γf	Расчетные нагрузки, кН/м2
Постоянные: собственный вес Вес пола: керамическая плитка цементная стяжка	2,5 0,3 0,44	1,1 1,1 1,2	2,75 0,33 0,53
ИТОГО g Временная V Полная q1=g+V	7	- 1,2	3,61 8,4 12,01

1.2     Определение усилий в сечении панели перекрытия

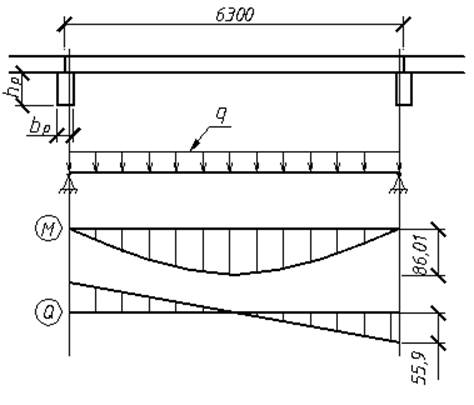a=7,2 м

L_p=7,2 м                                                            

b_p=0,3 м

Расчётный пролёт панели:

L₀=a-b/2=7,2-0,01=7,19 м

Равномерная распределённая нагрузка на перекрытие:

q=q₁·b_n=12,01·1,8=21,618 кН/м

Усилия от расчётной нагрузки:

Максимальный момент:

M_max=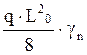==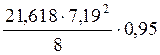132,71 кН·м²

Максимальное поперечное усилие:

Q_max=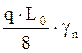==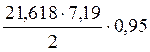73,83 кН

Размеры сечения плиты

h=42 см

b_кон=b_н -5 (ширина шва)=180-5=175 см

b'_f = b_кон-4=175-4=171 см

b_ср=(10+12)/2= 11 см

b=2·11=22 см – расчётная ширина ребра

h₀=h-a=42-4=38 см - рабочая высота сечения

h'_f =5 см – толщина верхней сжатой полки таврового сечения

Определение расчётной ширины полки b_f^’

1)   

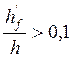
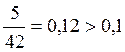 - условие выполнено

2) b_свеса=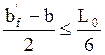       

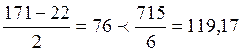 - условие выполнено

Оба условия выполнены, в расчет принимаем всю ширину полки

b_f’=b_кон=171 см

1.3     Расчет прочности нормальных сечений

Панель, предварительно напряженная, с одиночным армированием. Далее подбираем диаметр и количество стержней рабочей продольной арматуры.

α_m=M_max/(γ_b2·R_b·b'_f ·h₀²)=132,71·10³ /(0,9·17·171·38)=0,03

Зная α_m по таблице принимаем ξ=0,03, ζ=0,985

Проверяем условие ξ ≤ ξ_R

Задаёмся σ_sp

σ_sp+p ≤ R_sn

σ_sp-p ≥ 0,3·R_sn

 

R_sn=590 МПа

p=30+360/L=30+360/(7,15+0,5)=78,32 МПа

Принимаем σ_sp=472 МПа

Определяем предельное отклонение предварительного напряжения Δγ_sp:

Δγ_sp=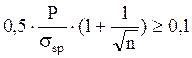, где n – количество стрежней продольной арматуры

Δγ_sp=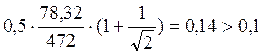

ω=0,85-0,008·R_b·γ_b2=0,85-0,008·17·0,9=0,73

ξ_R=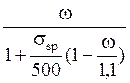==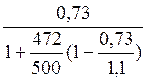0,712

ξ=0,03 < ξ_R=0,712 – условие выполняется

Коэффициент точности натяжения γ_sp=1-Δγ_sp=1-0,14=0,86

Определяем коэффициент условий работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести:

γ_s6=η-(η-1)(2ξ/ξ_R-1)=1,2-(1,2-1)(2·0,03/0,712-1)=1,11<1,2

здесь η=1,2 для арматуры класса АΙV

Находим требуемую площадь сечения растянутой арматуры :

A_SР=M/(ζ·R_S·γ_S6·h₀)=132,71·10³ /(0,985·510·1,11·38)=6,44 см²

По таблице подбираем ближайшую площадь A_SР=7,6 см², которую составляют 2 стержня диаметром 22 мм каждый.

1.4     Расчет прочности наклонных сечений.

Усилие обжатия:

N=P=A_sр·σ_sp

здесь:                   A_SР=7,6см²

                              σ_sp=0,8·R_sn=0,8·590=472 МПа

P=7,6·472=35,872 кН

Определяем коэффициент φ_n учитывающий влияние продольных сил:

φ_n=0,1·P/(R_bt·b·h₀)=0,1·3578,2/(1,2·22·38)=0,36<0,5 –условие выполняется

φ_f=0,75·15·5/(22·38)=0,07<0,5

h=1+ φ_n+ φ_f=1+0,36+0,07=1,43

, где

– для тяжёлого бетона

, где

– для тяжёлого бетона

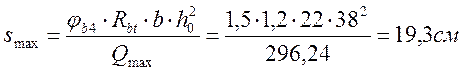>S

S=15 – на приопорных участках; S=30 – на средине пролёта

Принимаем поперечную арматуру класса В-I:   R_sw=260 МПа

d=5 мм

A _sw=0,392

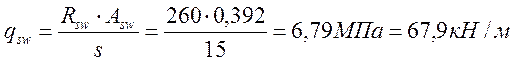
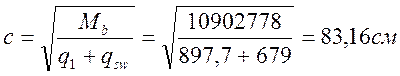
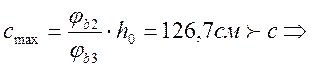
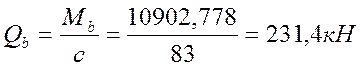
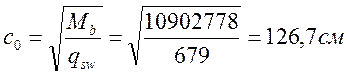
принимаем

Проверка:

– условие выполняется

, где

,где,

1.5     Расчет  полки  плиты на местный изгиб

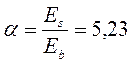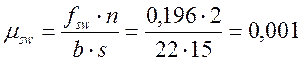
Плита работает по балочной схеме на изгиб только в одном направлении, т.е. в коротком. Расчетный пролет L₁=151 см

Нагрузка на 1м² полки может быть принята такой же, как и для плиты:

q = 9,4кН/м

Изгибающий момент для полосы шириной 1 м определяют с учетом частичной заделки в ребрах:

M=9,4·1,51²/11=1,95 кН·м

Принимаем арматуру класса Вр-I: Rs=365МПа, Es=170000МПа

α_m=M/R_b·γ_b2·b·h_o²=1950/(17·0,9·100·3,5²)=0,104

принимаем ζ=0,945

A_s=M/R_s·ζ·h_o=1950/365·3,5·0,945=1,64см² - 10Ø5 Bp-1 с As=1,96 см². Принимаем сетку  с поперечной рабочей арматурой Ø5 Bp-1 S=300 мм

1.6     Расчеты плиты по 2-ой группе предельных состояний.

1.6.1  Определение геометрических характеристик приведённого сечения.

бетон:

расчетное сопротивление осевому сжатию R_b=17 МПа;

коэффициент условий работы бетона γ_b2=0,9

арматура:

расчетное сопротивление растяжению арматуры R_s=510 МПа;

α=E_s/E_b=190000/32500=5,85

Находим площадь приведённого сечения

A_red=b'_f ·h'_f +b(h-h'_f)+αA_s=174·5+22(42-5)+5,85·7,6=1728,46 см²

Статический момент приведённого сечения относительно оси 1-1, проходящей по нижней грани сечения

S_red=b'_f ·h'_f(h-h'_f /2)+b(h-h'_f)·((h-h'_f )/2)+αA_sa=174·5(42-5/2)+22(42-5)·((42-5)/2)+5,85·7,6·4=49601,84 см³

Расстояние от центра тяжести приведённого сечения до оси 1-1

y₀=S_red/A_red=49601,84/1728,46=29 см

Момент инерции приведённого сечения относительно оси, проходящей через