

























































4. РЕГРЕССИОННЫЕ МОДЕЛИ ИССЛЕДОВАНИЯ
ЗАВИСИМОСТЕЙ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
Одно из основных назначений эконометрических моделей состоит в исследовании на эмпирических данных зависимостей между экономическими показателями. Используя эконометрические модели, можно оценить величину зависимости, ее надежность и форму связи. Выявление статистически значимой связи между показателями способно повысить эффективность воздействия управляющих параметров на развитие экономического объекта. Например, выявление статистически значимых факторов инфляции позволяет углубить понимание природы инфляционных процессов в экономике и на этой основе выработать эффективные мероприятия антиинфляционной политики. Или, пример на уровне предприятия. В результате изучения факторов, влияющих на объемы продаж, было выявлено более сильное влияние расходов на рекламу в сравнении с фактором снижения цен на продукцию. Это означает, что более эффективными с точки зрения влияния на объем продаж являются затраты в увеличение расходов на рекламу.
Наиболее простым и часто используемым видом эконометрических моделей является регрессионная модель, методика построения которой хорошо отработана.
4.1. Основы построения регрессионных моделей
Методическое обеспечение регрессионных моделей предполагает выявление набора потенциально возможных факторов, оказывающих влияние на динамику исследуемого показателя. Этот этап предполагает знание основных положений экономической теории, прикладной экономики, а также особенностей развития исследуемого экономического процесса. Далее, в рамках информационного обеспечения формируются ряды наблюдений, что предполагает сбор статистических данных по выделенному кругу показателей либо в пространстве (предприятия, цеха или отрасли), либо во времени (год, месяц, квартал). На данном этапе важным является обеспечение методологической сопоставимости данных в пределах ряда, что требует знания методологии составления статистической отчетности. В отличие от моделей МОБ и оптимизационных моделей, где математическое обеспечение ориентировано на исследование разрешимости и нахождение решения уже разработанных моделей, построение регрессионных моделей осуществляется непосредственно математическими методами, в частности методами математической статистики. В курсе «математическая статистика», например [1], дается математически строгое изложение методов статистического анализа данных. При изложении материала в данном учебном пособии приводятся лишь общие сведения из курса, которые являются минимально необходимыми для интерпретации статистических характеристик регрессионной модели и корректного ее использования. При изложении материала раздела приводятся лишь те статистические характеристики, которые непосредственно используются при оценке спецификации уравнения регрессии.
В данном учебном пособии рассматриваются вопросы построения регрессионных моделей на пространственных данных, методика разработки которых является наиболее простой. Особенности построения моделей на временных рядах представлены лишь обобщенно в виде замечаний. В пособии приведены лишь основные определения, формулы и другие минимально необходимые теоретические сведения для построения регрессионных моделей. Для углубленного изучения проблем построения регрессионных моделей можно рекомендовать литературу [10,19,28,29].
4.1.1. Особенности регрессионных моделей
Рассмотренные нами ранее модели были представлены функциональными зависимостями показателей, т.е. каждому значению показателя-фактора соответствует строго определенное значение результативного показателя. Например, в примере 1.2.1 имитационной модели налоговые поступления определялись ставками налога и соответствующими им налогооблагаемыми базами, а в примере 1.1.1 оптимизационной модели суточный расход ресурсов определяется объемом производства и нормами расхода ресурсов, выручка от реализации – ценой и объемами продаж. Функциональная зависимость имеет место тогда, когда результативный показатель зависит только от рассматриваемых факторов и никакие неучтенные факторы на него не оказывают влияние.
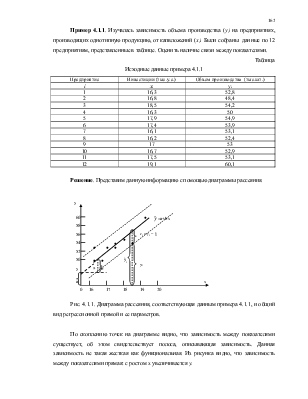
Но на практике при проведении аналитических исследований приходится рассматривать факторы, не позволяющие функционально описать динамику результативного показателя от факторов. Так, представляет экономический интерес исследование динамики объемов производства в зависимости от инвестиций. Очевидно, что помимо инвестиций на объем производства влияют и другие факторы: конечный спрос, уровень инфляции, динамика экономической конъюнктуры, система организации производства и т.д. В данном контексте невозможно зависимость указанных факторов на объем производства описать функционально. Поэтому в экономических исследованиях выделяют набор основных факторов и группу неучтенных факторов. В этом случае возможна ситуация, когда одинаковым значениям основного фактора x соответствует множество различных значений показателя y. Такого характера зависимости называются стохастическими, они и являются объектом построения эконометрических моделей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.