Нормально распределенные величины. Единичная матрица. Стандартная нормальная случайная величина

Пусть   – (условно) нормально распределенные случайные величины. Следовательно,

,                                        (42)

где  – единичная матрица размером .

Тогда и  (условно) нормально распределенные величины, а следовательно и векторная МНК-оценка  также условно нормально распределена (поскольку она линейна относительно ).

В силу  (20) и (24)

                                        (43)

Заметим, что 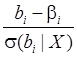 стандартная нормальная случайная величина, т.е.

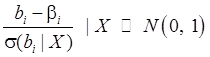                                                   (44)

Как было указано выше, случайная величина 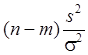  имеет распределение «хи квадрат» с числом степеней свободы :

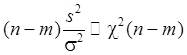                                                         (44’)

Кроме того, выше мы доказали, что вектор  и величина  независимы.

Следовательно, случайные величины 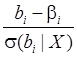 и 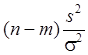 также независимы.

Поэтому с учетом (44) и (44’) случайная величина:

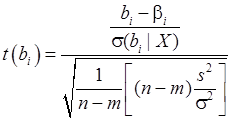                                    (44’’)

имеет распределение Стъюдента со степенями свободы  .

Упростив (44’’), получим:

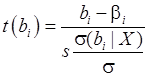                                                     (45)

Напомним, что распределение Стъюдента с  степенями свободы – это распределение следующей случайной величины:

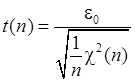,                                           (45’)    где  и  – независимые стандартная нормальная случайная величина и случайная величина, имеющая распределение «хи квадрат» с  степенями свободы.

Подставим  (26) в формулу (45) примет вид:

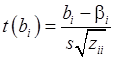                                    (45’’)

В силу (41’) формулу (45’’) запишем в виде:

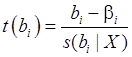                     (46)

Напомним, что  случайная величина  имеет распределение Стъюдента со степенями свободы  :

                                (47)

Статистики , как и в случае парной регрессии, можно использовать для проверки гипотез и для построения доверительных интервалов. (см. тему 2).  Отметим, что методика проверки гипотез и построения доверительных интервалов основана на использовании соотношения:

,                       (48)

где  двусторонняя квантиль распределения Стъюдента с числом степеней свободы  при уровне значимости .

Пусть .

В условиях нашего примера ,  и   .

Найдем t-статистики коэффициентов регрессии при  по формуле (46):

Как видно из таблицы, значимым коэффициентом является только .

Как и в случае парной регрессии доверительные интервалы для коэффициентов  имеют вид:

                        (49)

В нашем случае:

Проверка общего качества уравнения регрессии. Коэффициент детерминации

Напомним:

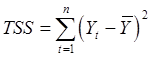,    (total sum of squares, полная сумма квадратов),               (50)

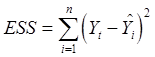,    (error sum of squares, остаточная сумма квадратов)        (51)

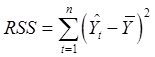,  (regression sum of squares, объясненная сумма квадратов)          (52)

В нашем случае:

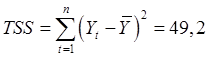
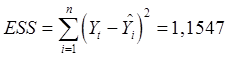
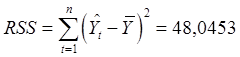
Обозначим:

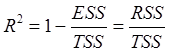                                                            (53)

Статистику  называют коэффициентом детерминации.

В нашем случае:

Чем больше значение  к 1, тем лучше качество подгонки.

Проверка гипотезы:

 – матрица размером ,  , ,

 – вектор-столбец длиной .

Пусть, например:

,     ,  

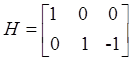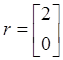Тогда гипотезу  можно записать в виде системы двух равенств:

Найдем

                                (54)

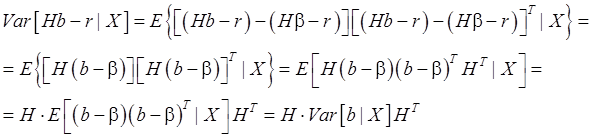
Итак,

            (55)

Подставим (24) в (55):

                        (56)

Итак,

                       (57)

Можно показать, что при выполнении гипотезы:

                                   (58)

величина:

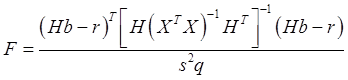                         (59)

имеет распределение Фишера (F-распределение) с  степенями свободы:

                                                        (60)

Напомним, что распределение Фишера с  степенями свободы – это распределение следующей случайной величины:

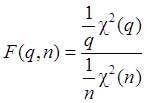                                                     (61)

где  и   – независимые случайные величины, имеющие распределения «хи квадрат» с  и  степенями свободы, соответственно.

Следовательно, при выполнении гипотезы (58) имеет место равенство:

,                                             (62)

где  – -квантиль распределения Фишера с  степенями свободы.

В случае, если  нулевая гипотеза отвергается; если , нет оснований отвергать нулевую гипотезу (и она принимается).

В условиях нашего примера при указанных выше ,  и   при :

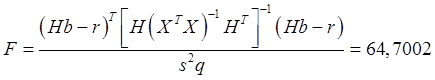
Следовательно, в данном случае нулевая гипотеза: ,     отвергается.

В частном случае, когда нулевая гипотеза имеет вид:

,                                   (63)

для модели: