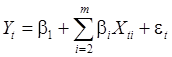
формулу (59) можно привести к виду:
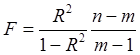 (64)
(64)
В условиях нашего примера:
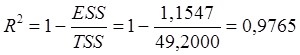
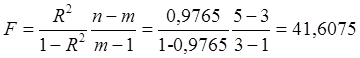
![]() .
.
Следовательно,
нулевая гипотеза: ![]() отвергается
отвергается
Рассмотрим случай, когда нулевая гипотеза имеет вид:
![]() ,
, ![]() , (65)
, (65)
где
![]() – некоторое
подмножество значений множества
– некоторое
подмножество значений множества ![]() индекса
коэффициентов
индекса
коэффициентов ![]() .
.
В
этом случае матрица ![]() будет
состоять из строк, в которых j-я компонента равна
1, а остальные – нули. Вектор
будет
состоять из строк, в которых j-я компонента равна
1, а остальные – нули. Вектор ![]() состоит
из нулей.
состоит
из нулей.
Например, в случае модели:
![]() (66)
(66)
и нулевой гипотезы:
![]() (67)
(67)
матрица
![]() и вектор
и вектор ![]() равны:
равны:
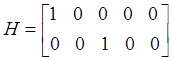 ,
, 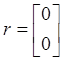
В рассматриваемом нами случае F-статистику (59) можно найти также следующим способом.
Наряду с исходной «длинной» моделью:
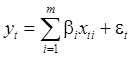 (68)
(68)
рассмотрим «короткую» модель:
![]() (69)
(69)
Например, в случае «длинной» модели (66) и нулевой гипотезы (67) «короткая» модель (69) имеет вид:
![]() (70)
(70)
Обозначим
через ![]() и
и ![]() остаточную сумму
квадратов и коэффициент детерминации для «длинной» регрессии, а через
остаточную сумму
квадратов и коэффициент детерминации для «длинной» регрессии, а через ![]() и
и ![]() – эти же величины
для короткой регрессии.
– эти же величины
для короткой регрессии.
Можно показать, что для F-статистики (59) справедливы формулы:
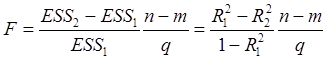 . (71)
. (71)
Напомним,
что количество степеней свободы F-статистики равно ![]() , где
, где ![]() – число равенств в
нулевой гипотезе.
– число равенств в
нулевой гипотезе.
Доверительная область для коэффициентов регрессии.
Рассмотрим
случай, когда ![]() .
.
Тогда
равенство (58) примет вид: ![]()
Заменив
![]() на
на ![]() и
и ![]() на
на ![]() в формуле (59),
получим:
в формуле (59),
получим:
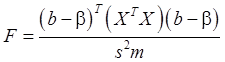 (72)
(72)
В
силу (62) ![]() -доверительная
область для вектора
-доверительная
область для вектора ![]() задается
условием:
задается
условием:
![]() (73)
(73)
и является эллипсоидом в m-мерном пространстве.
Доверительные интервалы для зависимой переменной
Пусть
![]() .
.
Например,
![]() .
.
Будем считать, что в соответствии с зависимостью (5), имеет место равенство:
![]() (74)
(74)
и
для ![]() выполняются
основные гипотезы линейной регрессии:
выполняются
основные гипотезы линейной регрессии:
1)
![]() ;
;
2)
![]() ;
;
3)
![]()
![]() .
.
В силу гипотезы (1):
![]() (75)
(75)
Прогнозное
значение ![]() находится в
соответствии с формулой (11):
находится в
соответствии с формулой (11):
![]() (76)
(76)
В
условиях нашего примера при ![]() :
:
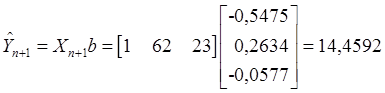
(При
этом реальное значение ![]() может не
известно.)
может не
известно.)
Заметим, что
![]() . (77)
. (77)
В
силу (20), (75), (76), прогнозное значение ![]() является
несмещенной оценкой величины
является
несмещенной оценкой величины ![]() ..
..
Для
получения доверительных интервалов ниже будем считать, что условное
распределение случайной величины ![]() нормально
(при фиксированных значениях случайных величин
нормально
(при фиксированных значениях случайных величин ![]() и
и ![]() ).
).
Тогда
в силу формулы (76) из того, что условное распределение оценки ![]() нормально,
вытекает, что условное распределение прогноза
нормально,
вытекает, что условное распределение прогноза ![]() также нормально.
также нормально.
При этом в силу (63):
![]() (78)
(78)
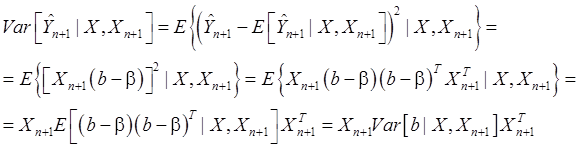
Итак,
![]() (79)
(79)
Подставив формулу (24) в (79), получим:
![]() (80)
(80)
Подставив
вместо ![]() ее выборочную
несмещенную оценку
ее выборочную
несмещенную оценку ![]() , получим
несмещенную оценку для
, получим
несмещенную оценку для ![]() :
:
![]() . (81)
. (81)
В условиях нашего примера:
![]()
Обозначим:
![]() (82)
(82)
В нашем случае:
![]()
Можно доказать, что статистика
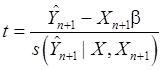 (83)
(83)
имеет
распределение Стъюдента с числом степеней свободы ![]() .
.
Следовательно,
при уровне значимости ![]() :
:
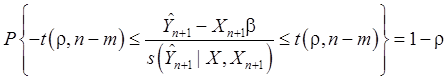 , (84)
, (84)
где
![]() – двусторонняя
квантиль распределения Стъюдента для уровня значимости
– двусторонняя
квантиль распределения Стъюдента для уровня значимости ![]() и числа степеней
свободы
и числа степеней
свободы ![]() .
.
Из (84) в результате несложных алгебраических преобразований имеем:
![]() (85)
(85)
Это
соотношение определяет доверительный интервал для ожидаемого значения ![]() :
:
![]() , (86)
, (86)
в
который с вероятностью ![]() попадает
попадает ![]() .
.
В
нашем случае 95%-й доверительный интервал для ![]() :
:
![]() .
.
Доверительный интервал для ![]()
Будем считать, что значение ![]() не известно.
не известно.
Из равенств (75), (77):
![]() (87)
(87)
Используя формулу (24), получим:
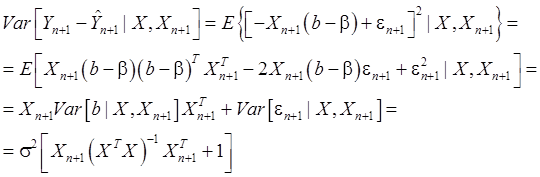
Итак,
![]() (88)
(88)
Следовательно,
![]() (89)
(89)
является несмещенной оценкой для ![]() .
.
В нашем случае:
![]()
Обозначим:
![]() (90)
(90)
В нашем случае:
![]()
Можно показать, что величина
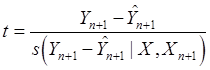 (91)
(91)
имеет
распределение Стъюдента с числом степеней свободы ![]() .
.
Следовательно,
при уровне значимости ![]() :
:
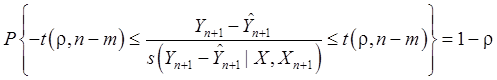 , (92)
, (92)
где
![]() – двусторонняя
квантиль распределения Стъюдента для уровня значимости
– двусторонняя
квантиль распределения Стъюдента для уровня значимости ![]() и числа степеней
свободы
и числа степеней
свободы ![]() .
.
Из (92) в результате несложных алгебраических преобразований имеем:
![]()
(93)
Это
соотношения определяет доверительный интервал для значения ![]() :
:
![]() , (94)
, (94)
в
который с вероятностью ![]() попадает
попадает ![]() .
.
В
нашем случае доверительный интервал для значения ![]() :
:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.