Симметричная положительно определенная матрица. Условие несмещенности прогноза, страница 3

Реализация ОМНК в случае гетероскедастичности

В этом случае матрица  диагональна.

Для оценки диагональных элементов матрицы  (т.е. дисперсий случайных отклонений ) можно использовать следующую методику.

Вначале используется классическая регрессионная модель: находятся соответствующие коэффициенты  (по формуле ),  прогнозные значения  и остатки   (для модели: ).

Затем строится (классическая) регрессия квадратов полученных остатков  на некоторые переменные :

,                                    (126)

где  – коэффициенты регрессии (126),  – случайные отклонения.

В качестве переменных  могут использоваться переменные , их квадраты, произведения , а также другие переменные.

Для коэффициентов  строится МНК-оценка:

                   (127)

и с помощью вектора  строятся оценки для дисперсий случайных отклонений :

                               (128)

С помощью полученных значений  строится диагональная матрица .

Затем матрицу  можно использовать вместо матрицы  для построения ОМНК-оценок и прогнозов.

Отметим, что при такой методике полагается, что:

                                              (129)

т.е. что  в гипотезе (3): . Следовательно, в формулах ОМНК можно считать, что .

Другой способ использования ОМНК в условиях гетероскедастичности (при отсутствии автокорреляции) состоит в следующем.

В качестве оценок коэффициентов регрессии используются МНК-оценки: .

Уайт показал, что матрица:

                                  (130)

является состоятельной оценкой матрицы  ковариаций оценок коэффициентов регрессии (т.е.  стремиться по вероятности к  при ).

Поэтому при реализации ОМНК можно использовать матрицу  (построенную по формуле (130)) в качестве оценки матрицы . Это касается вычисления оценок  по формуле (40) (и, следовательно, построения t-статистик и интервальных оценок для коэффициентов регрессии), построения F-статистики (формулы (48’), (50’), (51’)). (В указанных формулах следует использовать  вместо .)

Реализация ОМНК в случае автокорреляция остатков

Будем считать, что для модели:   последовательность случайных отклонений  образует авторегрессионный процесс первого порядка, т.е.

,                                    (131)

где  – последовательность независимых нормально распределенных величин с нулевым математическим ожиданием и постоянным стандартным отклонением ,  – коэффициент авторегрессии (причем ), – нормально распределенная случайная величина с нулевым математическим ожиданием и дисперсией , равной 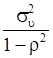 (при которой дисперсии  постоянны).

Используя равенство (131), несложно показать, что

                                       (132)

Из (132) следует, что  – это коэффициент корреляции  между  и , (в частности,   – это коэффициент корреляции  между  и ).

Обозначим:

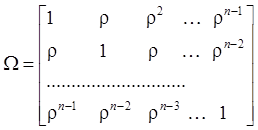                               (133)

матрицу состоящую из коэффициентов корреляции между  при разных значениях . (Элемент  этой матрицы равен .)

В силу (133) ковариационная матрица для вектора  равна:

,                              (134)

что согласуется с гипотезой (3).

При известном значении  матрица  легко находится по формуле (133). Следовательно, для оценки параметров модели: , проверки гипотез и построения прогноза можно использовать описанный выше ОМНК.

Однако в подавляющем большинстве случаев значение  неизвестно. В этих случаях используется (в частности) процедура Кохрейна-Оркатта (Cochrane-Orcutt). Изложим эту методику.

1)  Для исследуемой модели:  используется МНК и строится вектор остатков

2)  В качестве приближенного значения параметра  берется его МНК-оценка  в регрессии:

3)  С помощью оценки  параметра  строится оценка  матрицы ,

4)  С использованием матрицы   находятся  ОМНК-оценки , строятся прогнозные значения  и вектор остатков

5)  В качестве нового приближенного значения параметра  берется его МНК-оценка  в регрессии:

6)  Процедура повторяется, начиная с шага 3.

Процесс заканчивается, когда очередное приближение параметра  мало отличается от предыдущего (т.е. когда величина  достаточно мала; здесь индекс  обозначает номер итерации).