![]() (88)
(88)
![]() (89)
(89)
Подставим (87) в формула (84):
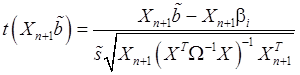 (90)
(90)
С учетом (89) формула (90) примет вид:
 (91)
(91)
Итак,
t-статистика Стъюдента для ![]() может быть найдена
по формуле (91) и
может быть найдена
по формуле (91) и
![]() (92)
(92)
Следовательно,
![]() (93)
(93)
Отсюда с учетом (91) и (81):
![]() (94)
(94)
Это
соотношение определяет интервал для ожидаемого значения ![]() :
:
![]() , (95)
, (95)
в
который с вероятностью ![]() попадает
попадает ![]() .
.
Интервальная
оценка для ![]()
Обозначим:
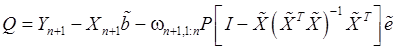 (96)
(96)
где
(в соответствии с вышеизложенным материалом) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Несложно показать, что формула (96) может быть также записана в виде:
![]() (96’)
(96’)
С помощью формулы (96) несложно показать, что
![]() (97)
(97)
Покажем независимость необъясненной дисперсии ![]() и случайной
величины
и случайной
величины ![]() :
:
В силу независимости ![]() и
и ![]() для этого
достаточно показать независимость
для этого
достаточно показать независимость ![]() и
случайной величины:
и
случайной величины:
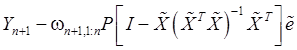 (98)
(98)
Поскольку
![]() функционально
зависит от вектора
функционально
зависит от вектора ![]() (формула
(22)) , для независимости случайной величины (98) и
(формула
(22)) , для независимости случайной величины (98) и ![]() достаточно показать
независимость величины (98) и вектора
достаточно показать
независимость величины (98) и вектора ![]() , а для этого
достаточно показать их некоррелированность (в силу того, что они нормально
распределены).
, а для этого
достаточно показать их некоррелированность (в силу того, что они нормально
распределены).
В силу (81):
![]() (99)
(99)
Подставим
(21’) и формулу: ![]() в (99),
в силу (54) получим:
в (99),
в силу (54) получим:
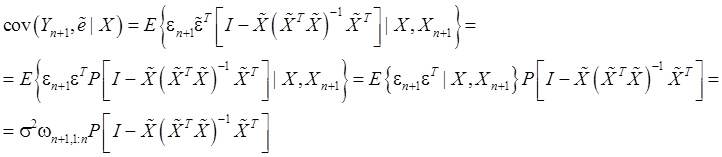 Итак,
Итак,
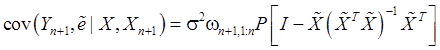 (100)
(100)
Из (100), (21’’):

Итак,
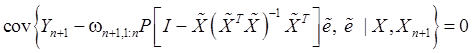 (101)
(101)
Отсюда
(в соответствии с вышеизложенным) вытекает независимость случайных величин ![]() и
и ![]() .
.
Обозначим
через ![]() стандартное
отклонение случайной величины (96).
стандартное
отклонение случайной величины (96).
В силу (97) :
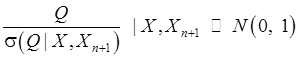 (102)
(102)
Напомним, что
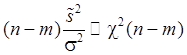 (103)
(103)
В силу независимости ![]() и
и ![]() случайная
величина:
случайная
величина:
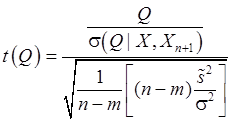 (104)
(104)
имеет
распределение Стъюдента со степенями свободы ![]() .
.
Упростив (104), получим:
 (105)
(105)
Найдем
![]() .
.
Подставим (52) в (96):
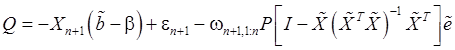 (106)
(106)
В
силу (106), (89), (14), (54) и с учетом независимости ![]() и
и ![]() получим:
получим:
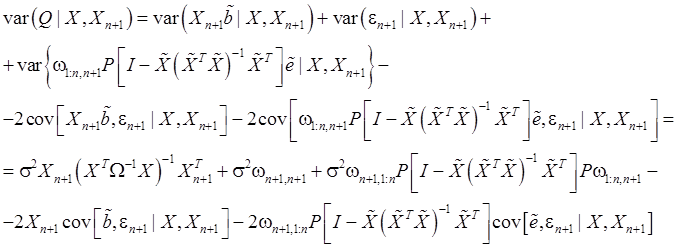
Итак,
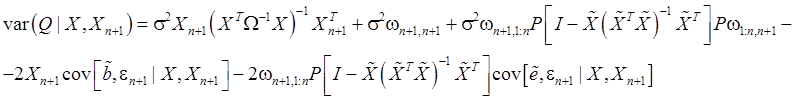 (107)
(107)
В соответствии с формулой (3.21):
![]() (108)
(108)
Следовательно,
в силу (54) и с учетом формулы ![]() получим:
получим:
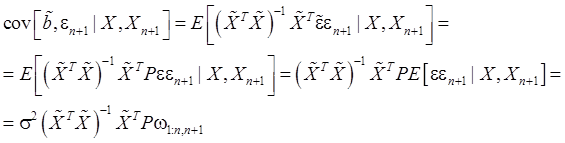
Итак,
![]() (109)
(109)
В
силу (54), (21’) и с учетом формулы ![]() получим:
получим:
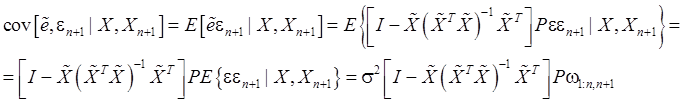
Итак,
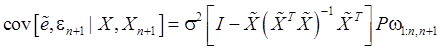 (110)
(110)
Подставим, (109), (110) в (107):
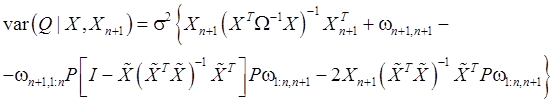 (111)
(111)
Подставив
формулы: ![]() ,
, ![]() в (111) получим:
в (111) получим:
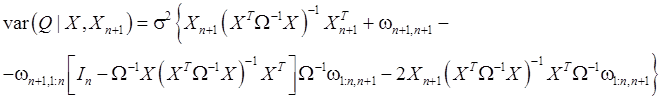 (112)
(112)
Обозначим:
 (113)
(113)
В силу (113) формулу (112) можно записать в виде:
![]() (114)
(114)
Из (114):
![]() (115)
(115)
В
силу (114), (115) для ![]() и
и ![]() можно использовать
оценки:
можно использовать
оценки:
![]() (116)
(116)
![]() (117)
(117)
Подставив формулу (115) в (105), с учетом (117) получим:
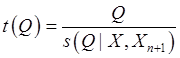 (118)
(118)
Напомним, что
![]() . (119)
. (119)
Следовательно,
![]() (120)
(120)
С учетом (79) формула (96’) примет вид:
![]() (121)
(121)
Обозначим:
![]() (122)
(122)
С учетом (122) формулу (121)можно записать в виде:
![]() (123)
(123)
Из (118), (120), (123) получим:
![]() (124)
(124)
Это
соотношение определяет прогнозный интервал для ![]() :
:
![]() , (125)
, (125)
в
который с вероятностью ![]() попадает
попадает ![]() .
.
В подавляющем
большинстве случаев матрица ![]() неизвестна.
неизвестна.
Однако можно делать
предположения о структуре этой матрицы. Например, в случае гетероскедастичности
(при отсутствии автокорреляции) матрица ![]() диагональна. Такие
предположения помагают оценить матрицу
диагональна. Такие
предположения помагают оценить матрицу ![]() .
.
В случае, когда
используется ОМНК с помощью оценки матрицы ![]() (поскольку сама
матрица
(поскольку сама
матрица ![]() не известна), ОМНК
называют практически реализуемым (либо доступным) ОМНК.
не известна), ОМНК
называют практически реализуемым (либо доступным) ОМНК.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.