Министерство образования Республики Беларусь
 БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра экономической информатики
 В.Ф.АЛЕКСЕЕВ
В.Ф.АЛЕКСЕЕВ
РЕШЕНИЕ ОПТИМИЗАЦИОННЫХ ЗАДАЧ
СРЕДСТВАМИ ЭЛЕКТРОННОЙ ТАБЛИЦЫ EXCEL
РЕШЕНИЕ ОПТИМИЗАЦИОННЫХ ЗАДАЧ
Термином "оптимизация" называют процесс или последовательность операций, позволяющих получить уточнённое решение. Хотя конечной целью оптимизации является отыскание наилучшего, или "оптимального", решения, обычно приходится довольствоваться улучшением известных решений, а не доведением их до совершенства. Те независимые переменные, от которых полностью и однозначно зависит решение задачи, называют "проектными параметрами" (в экономических задачах их называют "параметрами плана"). В качестве проектных параметров могут служить любые величины, служащие для количественного описания системы. Число проектных параметров различно в разных задачах и может быть любым. С увеличением этого числа растёт сложность задачи.
Ещё одно важное понятие, используемое в теории оптимизации – "целевая функция". Это выражение, зависящее от проектных параметров, которое надо сделать максимальным (или минимальным). К настоящему времени разработаны десятки алгоритмов, позволяющих численно решать задачи оптимизации. Часть этих алгоритмов включена в средство "Поиск решения".
Задание 1.
Собственные средства банка составляют 100 единиц. Банк получает прибыль, выдавая кредиты и покупая ценные бумаги. Доходность кредитов составляет 15%, ценных бумаг – 10%.
Таким образом, годовая прибыль банка составляет:
F(x, y)=0,15x+0,1y где x объем средств, выданных в виде кредитов, а y средства, затраченные на покупку ценных бумаг. Используя "Поиск решения" найти максимальную прибыль банка при условии ограничений:
x+ y≤100,
x≥ 35, y≥ 0,3*(x+ y) x≥ 0, y≥ 0.
Отступление. На этом примере можно показать различие между "линейными" и "нелинейными" задачами оптимизации. Если ни в одном выражении математической формулировки задачи (ни в целевой функции, ни в выражениях для ограничений) нет нелинейных операций с проектными параметрами (их перемножения, деления, возведения в степень, вычисления функций sin, cos, exp и т.п.), то задача называется линейной.
Если есть хотя бы одна нелинейная операция – задача нелинейная. В данном примере – задача линейная (ни в целевой функции, ни в дополнительных условиях нет нелинейных операций с проектными параметрами x и y).
(Сравните, например, с задачей в задании 3.3. В ней есть нелинейные операции с проектными параметрами в целевой функции: произведение, возведение в степень).
Применяя "Поиск решения" важно знать какая это задача – линейная или нелинейная, так как алгоритмы оптимизации могут различаться и применение линейных алгоритмов к нелинейным задачам (или наоборот) может привести к ошибкам. При решении линейных задач необходимо установить флажок "Линейная модель" в окне
"Параметры поиска решения"
Ещё одно важное для практики различие линейных и нелинейных задач: при решении линейных задач в качестве начальных приближений можно задать любые произвольные числа – решение всё равно будет найдено. А для нелинейных задач начальные приближения должны быть достаточно близки к решению. Рекомендации по выполнению.
Создать таблицу, как указано на рис. 1.
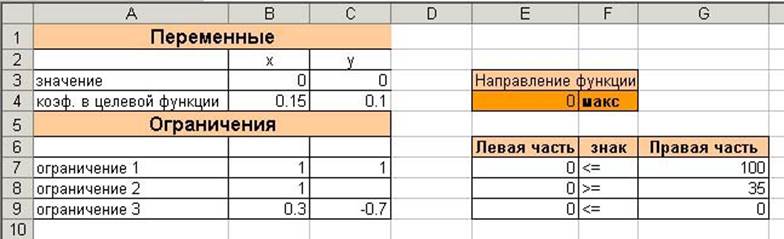
Для ячейки E4 введите формулу: =СУММПРОИЗВ($B$3:$C$3,B4:C4) и скопируйте
ее в ячейки E7, E8, E9.
Выполните команду Сервис/Поиск решения… Заполните вызванное окно в соответствии с рис. 2.
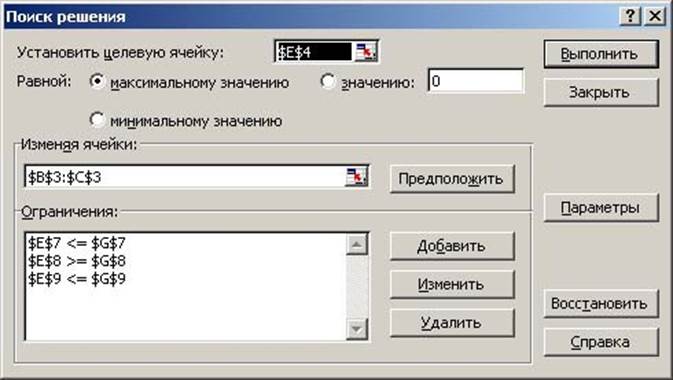
Ограничения записываются через использование кнопки Добавить, где вносятся обозначения ограничений задачи. (рис. 3)
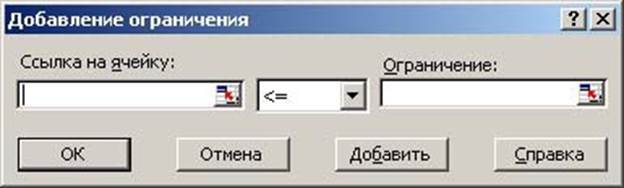
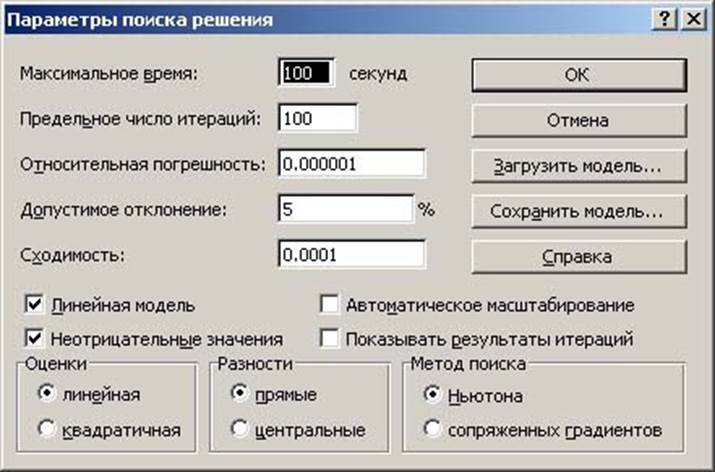
После заполнения окна Поиска решений… перейдите по кнопке Параметры в окно Параметры поиска решений (рис. 4) и установите там флажки напротив полей: Линейная модель и Неотрицательные значения.
Далее выполните команду ОК, и нажмите клавишу Выполнить в окне Поиска решений.
Если все выполнено правильно, то на экране появиться сообщение о найденном решении. (рис. 5)
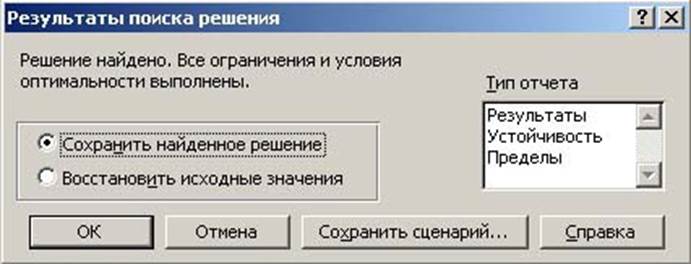
В результате выполнения задания должно появиться следующее решение данной оптимизационной задачи. (рис. 6)
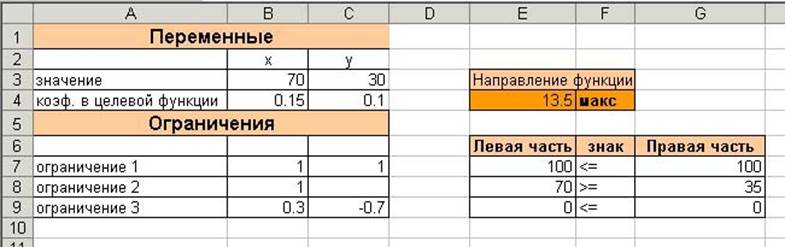
Переименуйте Лист 1 в задание_1 и сохраните файл под названием
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.