Геометрический смысл параметров. Криволинейные координаты. Соприкасающаяся плоскость и соприкасающаяся окружность

Можно определить производную поля v по полю w — производная будет не отдельным вектором, а векторным полем.

Лемма 7.1. f = const ⇔ df = 0, т.е. все частные производные равны 0.

Слева направо — очевидно. Наоборот:  функция f не зависит от x_i для ∀i ⇒ f = const.

Определение. Векторное поле v называется параллельным, если все его векторы параллельны, сонаправлены и одинаковы по длине.

Теорема 7.2. Векторное поле v = (X¹,...,Xⁿ) параллельно ⇔ ∇wv = 0 для всех векторов w в точках области.

Слева направо утверждение очевидно. Обратно: пусть ∇wv = 0. Тогда, в частности, ∇e_iv = 0. Значит,

. Следовательно, функции X^k не зависят от xⁱ для ∀i, а значит, они постоянны и все векторы поля постоянны.

Рассмотрим частный случай векторного поля v на кривой r(t), v = (X¹(t),...,Xⁿ(t)). Введём операцию как ^Dv_dt := (X^{˙ 1},...,X^{˙ n}), см. (2). Векторное поле v и координату t = x¹ можно локально продолжить до координат x¹,x²,...,xⁿ в области Rⁿ, тогда окажется (см. п. 7.1), что , ибо ввиду (3) .

Вывод:  - частный случай ∇wv.

7.3. Свойства операторов  в аффинном пространстве

0◦ Если v и w — гладкие векторные поля, то ∇wv - тоже гладкое поле, см. (3). 1^◦ Линейность по v^: ∇w(λv₁ + μv₂) = λ∇wv₁ + μ∇wv₂ ^для ∀λ,μ ∈ R.

Непосредственно следует из линейности операции дифференцирования по v, см. (3).

2◦ Формула Ньютона–Лейбница: ∇w(fv) = dwdf v + f∇wv, где f(x1,...,xn) — гладкая функция.

Пусть поле w имеет координаты (Y ¹,...,Y ⁿ). Имеем fv = (fX¹,...,fXⁿ). Тогда

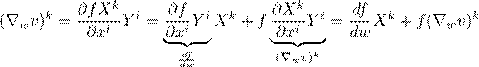                                              .      (4)

3◦ Функциональная линейность по w^: ∇fw_1+gw2v = f∇w₁v + g∇w₂v.

Умножение матрицы на вектор есть линейная операция, см. (3).  Теперь сформулируем свойства операции:

0◦ Если v — гладкое векторное поле, то  — гладкая функция по t, см. (2). 1◦ Линейность:

                                                                       .                              (5)

2◦ Формула Ньютона–Лейбница:

                                                                         (следствие(4)).                                 (6)

Свойство 3◦ операции ∇ для операции не определено.

7.4. Оператор ∇ на геометрическом многообразии (ковариантное дифференцирование)

Рассмотрим поверхность Mⁿ в пространстве и её касательное пространство TM в точке p. Предполагаем, что в случае псевдо-евклидова пространства на Mⁿ индуцируется риманова положительно определённая метрика. Пусть v — поле касательных векторов к поверхности, а w — некоторый касательный вектор. В определён оператор ∇wv. Поскольку операция ∇wv действует на v покоординатно, это следует из аргументов, приведённых в конце п. 7.1. В общем случае вектор ∇wv не касается поверхности Mⁿ (например, на сфере). Определим другую операцию дифференцирования в пределах касательных пространств. Тот оператор, который мы определили выше, будем обозначать через ∇⁰_wv, а новую операцию определим так:

                                                                                            ∇wv := Pr_TM ∇⁰_wv,                                                   (7)

где Pr_TM есть ортогональная проекция на касательное пространство TM.

Аналогичным образом для касательного векторного поля вдоль кривой r(t) ⊂ M определяется .

Перечислим свойства новой операции ∇wv. Легко видеть, что имеют место свойства 0◦-3◦, и доказательства их практически такие же (см. п. 7.3).

0◦ Пусть v и w - гладкие поля. Тогда ∇wv тоже гладкое.

Ортогонализуем базис в TM. Заметим, что это гладкий процесс (по отношению к координатам p). Поскольку касательные пространства не изотропны, то R^m = TM ⊕ TM⊥ в точках Mⁿ. Проекция — гладкая операция, а значит, и поле ∇wv будет гладким.  1◦ Линейность: проекция линейна, поэтому это свойство выполняется.

2◦ Формула Ньютона–Лейбница: из линейности проекции с учётом Pr_TMv = v. 3◦ Из линейности проекции

Покажем, что ∇ является внутренней операцией, что она выражается через метрический тензор G на Mⁿ.

7.5. Символы Кристоффеля и их свойства

Пусть поверхность Mⁿ в R^m_q задана параметрически уравнением r = r(x¹,...,xⁿ), yⁱ = yⁱ(x¹,...,xⁿ), где y¹,...,y^m — аффинные координаты в пространстве. Рассмотрим касательные поля v(X¹,...,Xⁿ) и w(Y ¹,...,Y ⁿ) на M, где Xⁱ = Xⁱ(x¹,...,xⁿ) и Y ⁱ = Y ⁱ(x¹,...,xⁿ) - координаты в базисе m₁,...,m_n ∈ TM, m_i = _∂x^∂r_i. Займёмся вычислением координат ∇wv, пользуясь свойтсвами 0◦- 3◦:

                                              .       (8)

Введём некоторые обозначения. Выражения Γ^k_ij := (∇m_jm_i)^k называются символами Кристоффеля