















































Можно определить производную поля v по полю w — производная будет не отдельным вектором, а векторным полем.
Лемма 7.1. f = const ⇔ df = 0, т.е. все частные производные равны 0.
Слева направо — очевидно. Наоборот: ![]() функция f не зависит от xi для ∀i ⇒ f = const.
функция f не зависит от xi для ∀i ⇒ f = const.
Определение. Векторное поле v называется параллельным, если все его векторы параллельны, сонаправлены и одинаковы по длине.
Теорема 7.2. Векторное поле v = (X1,...,Xn) параллельно ⇔ ∇wv = 0 для всех векторов w в точках области.
Слева направо утверждение очевидно. Обратно: пусть ∇wv = 0. Тогда, в частности, ∇eiv = 0. Значит,
![]() .
Следовательно, функции Xk не
зависят от xi для
∀i, а значит, они
постоянны и все векторы поля постоянны.
.
Следовательно, функции Xk не
зависят от xi для
∀i, а значит, они
постоянны и все векторы поля постоянны.
Рассмотрим частный случай векторного
поля v на кривой r(t),
v = (X1(t),...,Xn(t)).
Введём операцию ![]() как Dvdt := (X˙ 1,...,X˙ n), см. (2). Векторное поле v и координату t
= x1 можно
локально продолжить до координат x1,x2,...,xn в области Rn, тогда окажется (см. п.
7.1), что
как Dvdt := (X˙ 1,...,X˙ n), см. (2). Векторное поле v и координату t
= x1 можно
локально продолжить до координат x1,x2,...,xn в области Rn, тогда окажется (см. п.
7.1), что ![]() , ибо ввиду (3)
, ибо ввиду (3) ![]() .
.
Вывод: ![]() - частный случай ∇wv.
- частный случай ∇wv.
0◦ Если v и w — гладкие векторные поля, то ∇wv - тоже гладкое поле, см. (3). 1◦ Линейность по v: ∇w(λv1 + μv2) = λ∇wv1 + μ∇wv2 для ∀λ,μ ∈ R.
Непосредственно следует из линейности операции дифференцирования по v, см. (3).
2◦ Формула Ньютона–Лейбница: ∇w(fv) = dwdf v + f∇wv, где f(x1,...,xn) — гладкая функция.
Пусть поле w имеет координаты (Y 1,...,Y n). Имеем fv = (fX1,...,fXn). Тогда
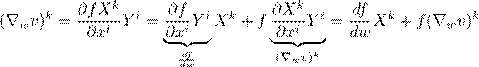 . (4)
. (4)
3◦ Функциональная линейность по w: ∇fw1+gw2v = f∇w1v + g∇w2v.
Умножение матрицы на вектор
есть линейная операция, см. (3). Теперь сформулируем свойства операции![]() :
:
0◦ Если v — гладкое векторное поле, то ![]() —
гладкая функция по t,
см. (2). 1◦
Линейность:
—
гладкая функция по t,
см. (2). 1◦
Линейность:
![]() . (5)
. (5)
2◦ Формула Ньютона–Лейбница:
![]() (следствие(4)). (6)
(следствие(4)). (6)
Свойство 3◦ операции ∇
для операции![]() не определено.
не определено.
Рассмотрим поверхность Mn в пространстве![]() и её
касательное пространство TM в
точке p. Предполагаем,
что в случае псевдо-евклидова пространства на Mn
индуцируется риманова положительно определённая метрика. Пусть
v — поле касательных
векторов к поверхности, а w —
некоторый касательный вектор. В
и её
касательное пространство TM в
точке p. Предполагаем,
что в случае псевдо-евклидова пространства на Mn
индуцируется риманова положительно определённая метрика. Пусть
v — поле касательных
векторов к поверхности, а w —
некоторый касательный вектор. В ![]() определён оператор ∇wv.
Поскольку операция ∇wv действует на v покоординатно, это следует из
аргументов, приведённых в конце п. 7.1. В общем случае вектор ∇wv не касается поверхности Mn (например, на
сфере). Определим другую операцию дифференцирования в пределах касательных
пространств. Тот оператор, который мы определили выше, будем обозначать через ∇0wv, а
новую операцию определим так:
определён оператор ∇wv.
Поскольку операция ∇wv действует на v покоординатно, это следует из
аргументов, приведённых в конце п. 7.1. В общем случае вектор ∇wv не касается поверхности Mn (например, на
сфере). Определим другую операцию дифференцирования в пределах касательных
пространств. Тот оператор, который мы определили выше, будем обозначать через ∇0wv, а
новую операцию определим так:
∇wv := PrTM ∇0wv, (7)
где PrTM есть ортогональная проекция на касательное пространство TM.
Аналогичным образом для касательного векторного поля вдоль
кривой r(t) ⊂ M определяется ![]() .
.
Перечислим свойства новой операции ∇wv. Легко видеть, что имеют место свойства 0◦-3◦, и доказательства их практически такие же (см. п. 7.3).
0◦ Пусть v и w - гладкие поля. Тогда ∇wv тоже гладкое.
Ортогонализуем базис в TM. Заметим, что это гладкий процесс (по отношению к координатам p). Поскольку касательные пространства не изотропны, то Rm = TM ⊕ TM⊥ в точках Mn. Проекция — гладкая операция, а значит, и поле ∇wv будет гладким. 1◦ Линейность: проекция линейна, поэтому это свойство выполняется.
2◦ Формула Ньютона–Лейбница: из линейности проекции с учётом PrTMv = v. 3◦ Из линейности проекции
Покажем, что ∇ является внутренней операцией, что она выражается через метрический тензор G на Mn.
Пусть поверхность Mn в Rmq задана параметрически уравнением r = r(x1,...,xn), yi = yi(x1,...,xn), где y1,...,ym — аффинные координаты в пространстве. Рассмотрим касательные поля v(X1,...,Xn) и w(Y 1,...,Y n) на M, где Xi = Xi(x1,...,xn) и Y i = Y i(x1,...,xn) - координаты в базисе m1,...,mn ∈ TM, mi = ∂x∂ri. Займёмся вычислением координат ∇wv, пользуясь свойтсвами 0◦- 3◦:
![]() . (8)
. (8)
Введём некоторые обозначения. Выражения Γkij := (∇mjmi)k называются символами Кристоффеля
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.