Определение и примеры метрических пространств. Изометрия. Выполнение аксиом

Точно так же понятие предельного перехода на плоскости или в многомерном пространстве основано на измерять расстояние между точками в соответствующих множествах. Мы введем далее понятие метрического пространства; тау будет названа совокупность объектов, для которых указаны взаимные «расстояния», удовлетворяющие некоторым естественным условиям. Наличие расстояний позволит ввести и изучить свойства предельного перехода «в чистом виде», т. е. независимо от природы элементов, участвующих в этом построении.

1. Определе ни е. Произвольное множество М некоторых элементов («точек») х, у, . . называется метрическим пространством,. если: 1) имеется правило, которое позволяет для любых двух точек х, у построить число ? (х, у) («расстояние от х до у»), 2) это правило удовлетворяет следующим требованиям (аксиомам):

1) ? (у, (х, у) для любых х и у (симметрия расстояния); 2) ? (х, при х + у; ? (х, для любого х;

З) ? (х, ? (х, у) А— ? (у, 2) для любых х, у, z (неравенство треугольника).

Примеры. 1. Любое множество М на вещественной прямой R1 является метрическим пространством с расстоянием ? (х, у) у (гл.

Точно так же множество М в плоскости R2 или в трехмерном пространстве Rз является метрическим пространством, если считать расстоянием между точками (для определенности и у— (Th, , Из) обычное геометрическое расстояние

Неравенство треугольника (аксиома З) здесь есть обычное геометрическое неравенство: третья сторона треугольника не больше суммы двух других сторон.

Аналогично в п-мерном пространстве Rп расстояние между точками , т, п) можно определить формулой

                                                                          (1)

поэтому любое множество М в п-мерном пространстве является метрическим пространством с расстоянием (1).

Выполнение аксиом 1 и 2 здесь очевидно. Для проверки выполнения аксиомы З применим неравенство Коши ¹ )

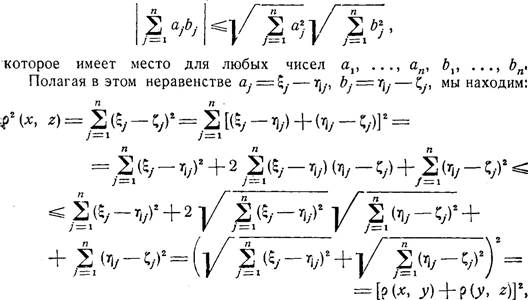
что и требуется.

¹ ) Приведем доказательство этого неравенства. Обозначим А

Ь), С Eajbj; нам нужно доказать, что

< АД

Это неравенство будет вЬшолнено, если многочлен второй степени

S 1 ] ОПРЕДЕЛЕНИЕ И примЕры                                                                                           ИЗОМЕТРИЯ 27

2. В задачах анализа, как правило, встречаются пространства, элементами которых являются функции (функциональные пространства).

Введение той или иной метрики в функциональных пространствах зависит от требований задачи. Когда имеется расстояние, то ясно, что близкими надо считать те элементы, расстояние между которыми мало. В анализе по большей части приходится начинать с обратного: по условиям задачи видно, какие элементы естественно считать близкими и соответственно этому каким образом следует вводить определение расстояния.

Например, часто бывает естественным считать непрерывные функции х (О и y (t) t<b) близкими, если мала величина тах х (О — у (О ! . Эту величину можно принять за определение расстояния между функциями х (0 и у (О; оно, очевидно, удовлетворяет аксиомам 1 — 3, и поэтому любое множество /VI непрерывных функций, определенных на отрезке [а, Ь], с введением расстояния по формуле

                                          ? (х, у)                   x(t) — у (t)                                    (2)

a<t<b

становится метрическим пространством.

З. В некоторых случаях (например, в вариационном исчислении), когда речь идет о функциях, имеющих производные до порядка К, естественно считать близкими такие элементы x(t) и у (О, у которых при всех значениях t близки не только значения самих функций, но и значения их производных до порядка К. Этому отвечает формула расстояния

(3)

Если взять некоторое множество функций х (О, имеющих непрерывные производные до порядка К, то с введением расстояния по формуле (З) оно становится, очевидно, метрическим пространством.

4.  В других случаях (например, в теории интегральных уравнений) естественно считать функции х (О и у (i) близкими, если они близки в интегральном смысле, т. е. если мала величина  S l x (i)

а не имеет различных веществеуных корней. Но

так что многочлен Р (1) может иметь не более одного вещественного корня

      Таким образом, неравенство         справедливо.

(гл. п

Здесь естественно ввести расстояние по формуле

                                                           х (О — у (t) dt.                              (4)

Очевидно, что аксиомы метрического пространства здесь также удовлетворяются.

5.  Иногда бывает нужно определять близость между функциями с помощью интеграла не от первой, а от какой-либо другой, например р-й, степени разности между этими функциями; соответствующее расстояние может быть задано формулой

                                        l x(t) — у (t) dt.                            (5)

При р 1 это определение также удовлетворяет аксиомам метрического пространства. Правда, проверка выполнения аксиомы З (за исключением простых случаев р и становится более сложной; мы ее приводить здесь не будем ^[1] ).

Таким образом, определение метрического пространства представляется достаточно гибким, чтобы удовлетворить самым разнообразным конкретным запросам математического анализа. В дальнейшем на материале всего нашего курса мы убедимся