Исследование функций с помощью производных. Условия возрастания и убывания функции

Условия возрастания и убывания функции

Изучим условия возрастания (не убывания) и убывания (не возрастания) функций. Напомним, что функция  y = f ( )x называется возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е. из неравенства x ₂ > x₁ следует неравенство f (x₂ ) > f (x₁). Функция называется убывающей на промежутке, если из  x ₂ > x₁ следует f (x₂ ) < f (x₁).

Функция  y = f ( )x называется неубывающей на промежутке, если из неравенства x ₂ > x₁ следует неравенство f (x₂ ) ≥ f (x₁), и невозрастающей, если из условия x ₂ > x₁ следует f (x₂ ) ≤ f (x₁).

(условия возрастания (убывания) монотонной функции). Если    f ′(x) > 0 на промежутке X , то функция y = f (x) возрастает на этом промежутке, если       f ′(x)< 0 на промежутке X , то функция y = f (x) убывает на этом промежутке.

◄Для функции y = f ( )x выполняются условия теоремы Лагранжа на отрезке [x₁;x₂ ]∈ X , поэтому существует точка x₀ ∈(x₁; x₂ ), в которой f (x₂ ) − f (x₁) = f′(x₀ )⋅(x₂ − x₁). Анализируем это равенство: если f ′(x₀ ) > 0, то из неравенства x₂ > x₁ следует неравенство f (x₂ ) > f (x₁) и обратно. Если же f (′x₀ )< 0, то из  x₂ > x₁ следует неравенство f (x₂ ) < f (x₁).►

Замечание 1. Обратное утверждение звучит несколько иначе. Если функция возрастает на промежутке, то f ′(x₀ )≥ 0 или не существует.

ПРИМЕР 1. Функция y = x³ возрастает на всей числовой оси, соответственно f ′(x) > 0, но в точке x = 0 производная  f ′(0) = 0.

⎧2x,   x ≥ 0,

             ПРИМЕР 2. Функция y = ⎨  не имеет производной в

⎩x, x < 0

точке х=0 (левая и правая производная различны), однако она возрастает при всех значениях х, в том  числе и в  точке х=0.

Замечание 2. Опираясь на более «мягкие» условия, можно сформулировать прямую  теорему: если производная функции, непрерывной на промежутке, неотрицательна, то функция на этом промежутке не убывает. Тогда прямая и обратная теоремы на формализованном языке звучат так:

для того, чтобы непрерывная на промежутке функция y = f (x) была неубывающей, необходимо и достаточно, чтобы

f (′x₀ )≥ 0.

Понятие экстремума

Определение. Точка x₀ называется точкой локального максимума функции f(x), если существует такая окрестность точки x₀ , что для всех х из этой окрестности f (x) ≤ f (x₀ ).

Определение. Точка x₀ называется точкой локального минимума функции f(x), если существует такая окрестность точки x₀ , что для всех х из этой окрестности f (x) ≥ f (x₀ ).

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Максимум и минимум функции называются ее локальными экстремумами (extremum – крайний).

Определение. Точка x₀ называется точкой строгого локального максимума (минимума) функции y = f ( )x , если для всех х  из окрестности точки x ₀ верно строгое неравенство f (x) < f (x₀ ) (соответственно f (x) > f (x₀ )).

Замечание. В приведенном определении локального экстремума мы не предполагаем непрерывности функции  в точке x₀ .

⎧x²,  x ≠ 0,

             ПРИМЕР. Функция  y = ⎨    разрывна в точке х=0, но

⎩1,    x = 0

имеет в этой точке максимум, поскольку существует окрестность точки х=0, в которой f (x) < f (x₀ ).

Наибольшее (наименьшее) значение функции на промежутке называется глобальным экстремумом. Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Необходимое условие экстремума

  (о необходимом условии экстремума).

Если функция  y = f (x) имеет экстремум в точке x₀ , то ее производная f ′(x₀ ) либо равна нулю, либо не существует.

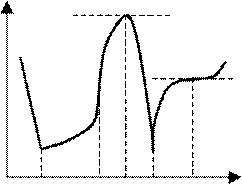◄Если в точке x₀ функция имеет экстремум и дифференцируема, то в y некоторой окрестности этой точки y = f ( x)

выполнены    условия теоремы Ферма, следовательно, производная функции в этой

точке равна нулю.                                                          x

Но функция y = f ( )x может иметь ^{x1 x}₂ ^x₃ ^x₄ ^x₅ экстремум и не быть