![]()
Теоремы Ферма, Ролля, Лагранжа, Коши
Раскрытие неопределенностей (правило Лопиталя)
Сравнение функций по скорости роста
Формулы Маклорена и Тейлора
Ряды Маклорена для элементарных функций
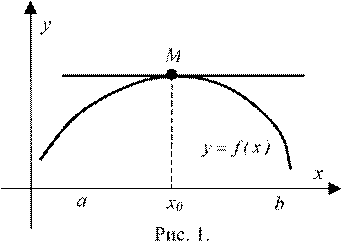
![]() (о равенстве нулю производной). Пусть функция y = f (x):
(о равенстве нулю производной). Пусть функция y = f (x):
1) дифференцируема на интервале (a;b), 2) достигает экстремума в точке x0 ∈(a;b).
Тогда производная функции в этой точке f ′(x0) = 0.
![]()
◄Пусть функция y=f(x) дифференцируема на интервале (a;b) и в точке x0 принимает наибольшее значение при x0 ∈(a;b). По f(x)− f(x0 )
определению
производной f (′x0 ) = lim ![]() ,
причем предел
,
причем предел
x→x0 x − x0
не зависит от того, будет ли x → x0 справа или слева. Но при x > x0 f (x) − f (x0)
![]() ≤ 0, откуда следует, что
f ′(x0 )≤ 0. При x < x0 имеем x − x0 f (x) − f (x0)
≤ 0, откуда следует, что
f ′(x0 )≤ 0. При x < x0 имеем x − x0 f (x) − f (x0)
![]() ≥
0, следовательно,
f ′(x0 )≥ 0. x − x0
≥
0, следовательно,
f ′(x0 )≥ 0. x − x0
По условию функция y=f(x) дифференцируема в точке x0, следовательно, ее предел при x → x0 не должен зависеть от выбора направления приближения аргумента х к точке x0, т.е. f(x)− f(x0 ) f(x)− f(x0 )
![]()
![]() =
lim
=
lim ![]() = f ′(x0 )
= f ′(x0 )
xx − x0 x→x0−0 x − x0
⎧ f (′x0 )≤ 0
Получаем систему ⎨ , из
⎩ f (′x0 )≥ 0
которой следует f ′(x0 ) = 0. Аналогично рассматривается другой случай.► Геометрический смысл теоремы Ферма очевиден: в точке наибольшего или наименьшего значения касательная к графику функции параллельна оси абсцисс.
 (о производной функции,
принимающей на концах отрезка равные значения). Пусть функция y = f (x)
(о производной функции,
принимающей на концах отрезка равные значения). Пусть функция y = f (x)
1) непрерывна на отрезке [a;b];
2) дифференцируема на интервале (a;b);
3) на концах отрезка [a;b] принимает равные значения:
f(a) = f(b).
Тогда на интервале (a;b) найдется по крайней мере одна точка x0, в которой f ′(x0 ) = 0.
![]()
◄Функция у=f(x) непрерывна на отрезке [a;b]. В силу второй теоремы Вейерштрасса она на этом отрезке принимает наименьшее и наибольшее значения. Пусть это будут значения m и M. Могут представиться два случая:
1) M = m. В этом случае m ≤ f (x) ≤ m, функция у=f(x) является постоянной на отрезке [a;b]. Поэтому f'(x) = 0 во всем интервале (a;b), теорема верна.
2) M > m. Тогда для функции у=f(x) даже в том крайнем случае, когда, например, наибольшее значение функции принимается на конце отрезка f(a) = f(b) = M, наименьшее значение будет приниматься уже внутри отрезка. Следовательно, найдется точка x0 ∈(a;b), в которой f(x0) = m. Но тогда по теореме Ферма f ′(x0 ) = 0.►
![]()
Теорема Ролля имеет простой геометрический смысл: найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.
Если f(a) = f(b) = 0, то теорему Ролля можно сформулировать так: между двумя последовательными нулями дифференцируемой функции имеется хотя бы один нуль производной.
![]()
![]() (о конечных приращениях).
(о конечных приращениях).
Пусть функция y = f (x)
1) непрерывна на отрезке [a;b];
2) дифференцируема на интервале (a;b).
Тогда на интервале (a;b) найдется
по крайней мере одна точка x0 такая, y B
f (b) − f (a)
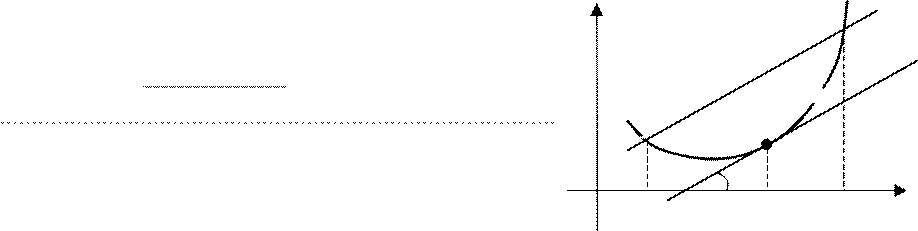 что = f ′(x0). y
= f(
x)
что = f ′(x0). y
= f(
x)
b −a
A M
◄Введем вспомогательную функцию
L(x) на отрезке [a;b], определив ее так: ϕx
f (b) − f (a) a x0 b
![]() L(x) = f(x)-f(a)- (x
− a). Рис. 2
L(x) = f(x)-f(a)- (x
− a). Рис. 2
b − a
Эта функция на [a;b] удовлетворяет условиям теоремы Ролля:
1) она непрерывна на [a;b], поскольку непрерывны все слагаемые L(x);
2) на (a;b) функция L(x)имеет производную;
3) L(a) = L(b) = 0.
Из теоремы Ролля следует, что существует точка x0 ∈(a;b), в
f(b)− f(a)
которой L′(x0 ) = 0. Следовательно, L′(x0 ) = f (′x0 )- ![]() =
0. b − a f(b)−
f(a)
=
0. b − a f(b)−
f(a)
Отсюда f (′x0 ) = ![]() ,
x0 ∈(a;b).► b − a
,
x0 ∈(a;b).► b − a
Геометрический смысл
теоремы Лагранжа. Отношение f
(b) −
f (a) ![]() есть
угловой коэффициент хорды АВ, а f ′(x0 ) есть
есть
угловой коэффициент хорды АВ, а f ′(x0 ) есть
b − a
угловой коэффициент касательной к кривой у=f(x) в точке с абсциссой x0 (рис.2). Утверждение теоремы Лагранжа сводится к следующему: на кривой у=f(x) точка M(x0;f(x0 )) такая, что через эту точку можно провести касательную, параллельную хорде AB.
Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде: f(b) − (a) = f′(x0)⋅(b − a).
![]()
![]() (об отношении конечных приращений двух функций).
(об отношении конечных приращений двух функций).
Если функции y = f (x) и y = g(x)
1) непрерывны на отрезке [a;b];
2) дифференцируемы на интервале (a;b);
3) производная g′(x) ≠ 0 на интервале (a;b).
Тогда на интервале (a;b) найдется по крайней мере f (b) − f (a) f ′(x0)
![]() одна точка x0
такая, что =
. g(b)
− g(a)
g′(x0)
одна точка x0
такая, что =
. g(b)
− g(a)
g′(x0)
◄Из условия теоремы следует, что g′(x) ≠ 0. Это означает, что разность g(b) − g(a) ≠ 0. Действительно, если бы g(b) − g(a) = 0, то функция y=g(x), являясь непрерывной и дифференцируемой, удовлетворяла бы условиям теоремы Ролля и в таком случае g′(x) была бы равна нулю по крайней мере в одной точке x0 интервала (a;b), что противоречит условию. Введем вспомогательную
f(b) - f(a)
функцию K(x)
=
f(x) -f(a) - ![]() (g(x) − g(a)). g(b) − g(a)
(g(x) − g(a)). g(b) − g(a)
Эта функция удовлетворяет всем условиям теоремы Ролля:
1) K(x) непрерывна на отрезке [a;b], так как непрерывны функции у=f(x) и y=g(x);
2) функция K(x) имеет производную всюду в интервале (a;b), поскольку каждое слагаемое в правой части функции K(x) имеет производную на этом интервале;
3) K(a) = K(b) = 0, в чем убеждаемся непосредственной проверкой.
Из теоремы Ролля делаем вывод о существовании точки x0 ,
f (b) − f (a)
что K′(x0 ) = 0. Поэтому K′(x0 ) = f ′(x0 ) − ![]() g′(x0 ) = 0. g(b) − g(a)
g′(x0 ) = 0. g(b) − g(a)
f ′(x0 ) f (b) − f (a)
![]() Отсюда следует = .►
Отсюда следует = .►
g′(x0 ) g(b) − g(a)
Теорема Лагранжа является частным случаем теоремы Коши: достаточно в теореме Коши взять g(x) = x.
![]() ( нахождения предела отношения функций через предел отношения их производных).
( нахождения предела отношения функций через предел отношения их производных).
Пусть функции y = f(x) и y = g(x)
1)дифференцируемы в окрестности точки a, кроме, быть может, самой точки a;
2)g(x) ≠ 0 и g′(x) ≠ 0 в этой окрестности;
3)lim f (x) = 0, lim g(x) = 0;
x→a x→a
f ′(x)
4)существует lim ![]() (конеч. или беск.)
(конеч. или беск.)
x→a g′(x)
f (x) f (x) f ′(x)
![]() Тогда существует lim ,
причем lim = lim x→a g(x) x→a g(x) x→a g′(x)
Тогда существует lim ,
причем lim = lim x→a g(x) x→a g(x) x→a g′(x)
◄В теореме ничего не сказано о значениях y = f(x) и y = g(x) в точке х=а. Положим f(a) = g(a) = 0. Так как теперь lim f (x) = f (a)
x→a
и lim g(x) = g(a), то функции y = f(x) и y = g(x) будут непрерывны
x→a
в точке а. Поэтому на отрезке [a;x], где х - какая угодно
точка окрестности точки а, функции y = f(x) и y = g(x)
удовлетворяют всем условиям теоремы Коши. Следовательно, между а и х
найдется по крайней мере одна точка ![]() х f (x) f (x) − f (a) f ′(x0 ) a x0 x
х f (x) f (x) − f (a) f ′(x0 ) a x0 x
![]() x0
такая, что = = .
x0
такая, что = = .
g(x) g(x) − g(a) g′(x0 ) Рис. 3. Величина x0 зависит от х, причем при x → a точка x0 также
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.