Ранг системы векторов, базисы и линейная зависимость между векторами

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УО «Белорусский государственный экономический университет»

, ,

ВЫСШАЯ МАТЕМАТИКА

Учебно-методическое пособие

для студентов дневной формы обучения

Контрольная работа № 1

 по теме «Линейная алгебра»

МИНСК 2008

ТРЕБОВАНИЯ ПО ОФОРМЛЕНИЮ

КОНТРОЛЬНОЙ РАБОТЫ

Студент должен выполнить контрольную работу, строго придерживаясь указанных ниже правил. Работа, выполненная без их соблюдения, к защите не допускается и возвращается студенту на доработку.

Номер варианта выполненной контрольной работы должен совпадать с порядковым номером в журнале старосты группы. Контрольная работа, выполненная не по своему варианту заданий, не зачитывается.

1. Контрольную работу следует выполнять в отдельной тетради, оставляя поля для замечаний рецензента.

2. В заголовке работы должны быть разборчиво написаны фамилии и инициалы студентов, номер зачетной книжки (шифр), номер группы, номер контрольной работы. Заголовок работы нужно поместить на обложке тетради.

3. Условия всех задач нужно записывать полностью. В том случае, если задача имеет общую формулировку, ее условие следует переписывать, заменяя общие данные конкретными из соответствующего номера варианта.

4. Решения задач следует располагать в порядке номеров, указанных в заданиях.

5. Решения задач следует излагать подробно и аккуратно, объясняя все действия и делая необходимые чертежи.

6. В конце работы нужно указать использованную литературу.

7. После получения отрецензированной работы студент должен исправить все отмеченные ошибки и недочеты и вернуть ее на повторное рецензирование. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для исправлений и дополнений в соответствии с указаниями рецензента.

КОНТРОЛЬНАЯ РАБОТА № 1

Вариант №1

1. Вычислить определитель матрицы:

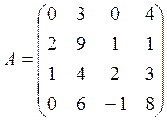
2. Решить систему:

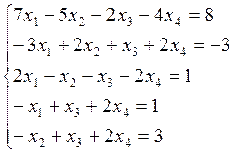
3. Найти ранг системы векторов, базисы и линейную зависимость между векторами:

    

    

4. Решить матричное уравнение XA = B, где

      

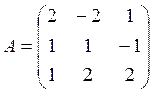
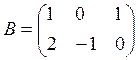
5.Даны четыре вектора:

    

    

Показать, что в векторы     образуют базис в трехмерном пространстве и найти координаты вектора      в этом базисе.

Вариант №2

1. Вычислить определитель матрицы:

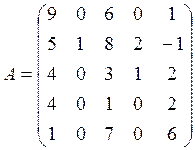
2. Решить систему:

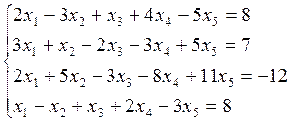
3. Найти ранг системы векторов, базисы и линейную зависимость между векторами:

    

    

4. Решить матричное уравнение XA -2B = C, где

          

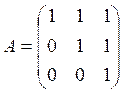
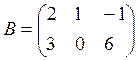
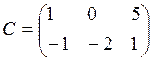
5. Даны четыре вектора:

    

    

Показать, что в векторы     образуют базис в трехмерном пространстве и найти координаты вектора      в этом базисе.

Вариант №3

1.Вычислить определитель матрицы:

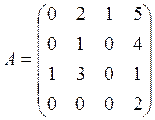
2. Решить систему:

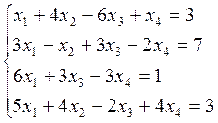
3.Найти ранг системы векторов, базисы и линейную зависимость между векторами:

    

    

4. Решить матричное уравнение XA = B, где

    

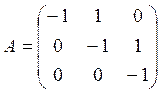
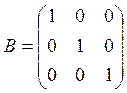
5.Даны четыре вектора:

    

    

Показать, что в векторы     образуют базис в трехмерном пространстве и найти координаты вектора      в этом базисе.

Вариант №4

1.Вычислить определитель матрицы:

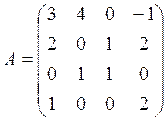
2.Решить систему:

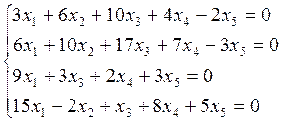
3.Найти ранг системы векторов, базисы и линейную зависимость между векторами:

    

    

4. Решить матричное уравнение AX + B = C, где

          

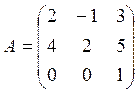
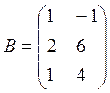
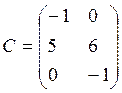
5.Даны четыре вектора:

    

    

Показать, что в векторы     образуют базис в трехмерном пространстве и найти координаты вектора      в этом базисе.

Вариант № 5

1. Вычислить определитель матрицы:

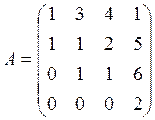
2. Решить систему:

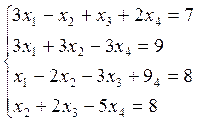
3. Показать, что система векторов линейно зависима, найти базисы и линейную зависимость между векторами:

    

4.Решить матричное уравнение XA = B, где

    

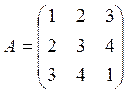
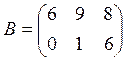
5.Даны четыре вектора:

    

    

Показать, что в векторы     образуют базис в трехмерном пространстве и найти координаты вектора      в этом базисе.

Вариант №6

1.Вычислить определитель матрицы:

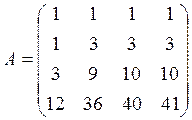
2.Решить систему:

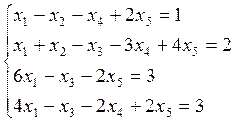
3.Найти ранг системы векторов, базисы и линейную зависимость между векторами:

    

    

4.Решить матричное уравнение 4C-XA = 2B, где

          

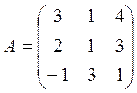
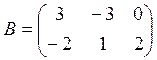
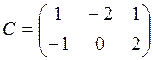
5.Даны четыре вектора:

     

    

Показать, что в векторы     образуют базис в трехмерном пространстве и найти координаты вектора      в этом базисе.

Вариант №7

1.Вычислить определитель матрицы:

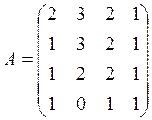
2. Решить систему:

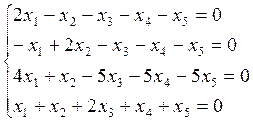
3. Показать, что система векторов линейно зависима, найти базисы и линейную зависимость между векторами:

    

          

4. Решить матричное уравнение:

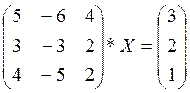
5. Даны четыре вектора:

    

    

Показать, что в векторы     образуют базис в трехмерном пространстве и найти координаты вектора      в этом базисе.

Вариант №8

1. Вычислить определитель матрицы:

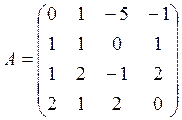
2. Решить систему:

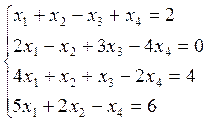
3. Показать, что система векторов линейно зависима, найти базисы и линейную зависимость между векторами:

    

    

4. Решить матричное уравнение AXB = C, где

          

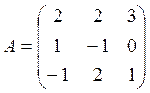
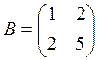
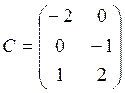
5. Даны четыре вектора:

    

    

Показать, что в векторы     образуют базис в трехмерном пространстве и найти координаты вектора      в этом базисе.

Вариант №9

1. Вычислить определитель матрицы:

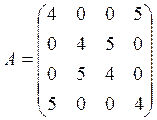
2. Решить систему:

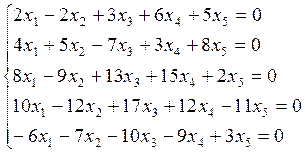
3. Найти ранг системы векторов, базисы и линейную зависимость между векторами:

    

    

4. Решить матричное уравнение XA = B, где

    

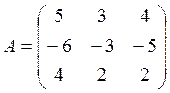
5. Даны четыре вектора:

    

    

Показать, что в векторы     образуют базис в трехмерном пространстве