











Понятие числового ряда и его сходимости
|
Пусть дана бесконечная последовательность чисел a1,a2,a3,...,an,... . Числовым рядом называется выражение
|
Что есть сумма ряда ???
 Отличается
от суммы конечного числа слагаемых. Например, сочетательное свойство может нарушаться:
Отличается
от суммы конечного числа слагаемых. Например, сочетательное свойство может нарушаться:
(1−1)+ (1−1)+ (1−1)+..... = 0+ 0+0+.... = 0
1−(1−1)−(1−1) −..........=1−0−0−........ =1
Для корректного определения суммы бесконечного ряда воспользуемся операцией предельного перехода.
|
Определение. |
Частичной n― ой суммой ряда (1) сумма Sn его первых n членов: Sn = a1 + a2 +...+ an. |
|
|
называется |
Образуем теперь последовательность
S1,S2,...Sn,..., состоящую из частичных сумм ряда (1).
|
Определение. |
Если существует конечный предел S частичных сумм S= lim Sn, то n→∞ сходящимся, а число S ― суммой записывается этот факт как S n=1 |
|
|
последовательности ряд (1) называется ряда и |
Если lim Sn не существует или равен бесконечности, n→∞ то ряд (1) называется расходящимся.
|
Пример. |
1) Исследовать на сходимость ряд +1`−1+........ т.е общий член есть an = (−1)n |
|
|
1−1 |
Решение. Так как последовательность частичных сумм имеет вид
S1 =1,S2 =1−1= 0,S3 =1−1+1=1,.....,Sn = (−1)n+1 то lim Sn не существует ⇒ ряд расходится n→∞
|
Пример. |
2) Исследовать на сходимость (по !) ряд
ряд сходится, то найти его сумму. |
|
|
определению и, если |
Решение. Общий член ряда an = 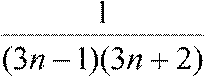
представим в виде двух слагаемых
1 a b
![]() = + и найдем
числа a и b
= + и найдем
числа a и b
(3n −1)(3n + 2) 3n −1 3n + 2
методом неопределенных коэффициентов:
1 n(3a + 3b) + 2a −b
![]() = .
= .
(3n −1)(3n + 2) (3n −1)(3n + 2)
⎧3a +3b = 0, ⎧ b = −a, ⎧b = −1 3,
![]() ⎨ ⇔ ⎨ ⎨
⎨ ⇔ ⎨ ⎨
⎩2a −b =1, ⎩2a + a =1, ⎩a =1 3.
Значит,
an 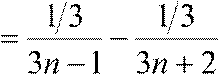 , а тогда
, а тогда
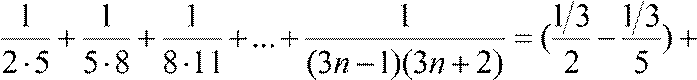
(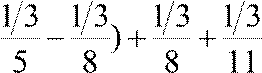 )+...+ (
)+...+ (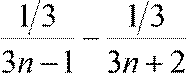 ).
).
|
В этой сумме все слагаемые, кроме первого и последнего, взаимно уничтожаются. |
||
|
Sn =
|
. |
|
Находим теперь
![]() 1 1
3 1 1 1 1 1
1 1
3 1 1 1 1 1
![]() lim
( − ) = − lim = − ⋅0 =
lim
( − ) = − lim = − ⋅0 =
n→∞ 6 3n + 2 6 3n→∞ 3n + 2 6 3
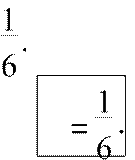 Итак, данный ряд сходится
и его сумма равна S
Итак, данный ряд сходится
и его сумма равна S
∞
Ряд a + aq + aq2 +...+ aqn−1 +... = ∑aqn−1,a≠ 0, (2)
n=1
составленный из членов геометрической прогрессии со знаменателем q, называется геометрическим рядом.
 Если
q <1, то
ряд (2) сходится и его сумма равна a
Если
q <1, то
ряд (2) сходится и его сумма равна a
S = ; если q ≥1, то ряд (2) расходится.
1− q
Д-во:
n n
a − aq a − aq a
Sn = ![]() ⇒ lim
⇒ lim ![]() = (q <1) =
= (q <1) = ![]()
1− q n→∞ 1− q 1− q
Ряд , называемый
2 3 n n=1 n
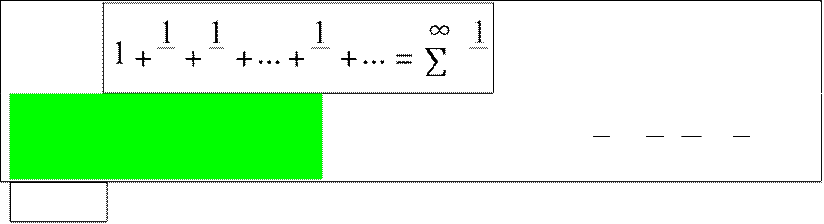 гармоническим рядом, расходится.
⎜ = ( + )⎟
гармоническим рядом, расходится.
⎜ = ( + )⎟
⎝c 2 a b ⎠
Док-во. От противного. Пусть lim Sn =S. Тогда n→∞
lim (S2n −Sn) = lim S2n − lim Sn =S−S = 0. n→∞ n→∞ n→∞
Но с другой стороны
 (S2n − Sn) =
(S2n − Sn) = ![]() . Тогда n 2 2n 2
. Тогда n 2 2n 2
равенство lim (S2n −Sn) = 0 невозможно.Противоречие n→∞
|
Обобщенный гармонический ряд если p >1 и расходится, если p ≤ |
|
сходится, |
||
|
1. |
УПР* Доказать |
|||
|
Простейшие свойства сходящихся рядов. |
|||||
|
Определение 1 |
. Если в ряде (1) отбросить первые n получится ряд rn, называемый остатком n-го члена: |
||||
|
членов, то ряда (1) после rn |
|||||
|
|
(3) |
||||
|
. Если ряд (1) сходится, то сходится и любой и, наоборот, если остаток (3) сходится, то ряд (1). |
||
|
его остаток сходится и |
|
Определение 2. |
Произведением ряда (1) на постоянное ряд ca1 +...+can n=1 |
|
|
число c называют |
|
Если ряд (1) сходится и его сумма равна S, сходится и его сумма равна cS. |
|||
|
то и ряд (4) |
||||
|
Определение 3. |
Суммой (разностью) двух рядов ∞ ∞ +...= ∑an и b1 + b2 +...+ bn +...= ∑bn n=1 n=1
|
|||
|
a1 + a2 +...+ an называется ряд |
||||
|
∞ ∞ . Если ряды ∑an и ∑bnсходятся и имеют n=1 n=1 и S2, соответственно, то их сумма и разность имеют суммы S1± S2. |
||
|
суммы S1 сходятся и |
Как вычислить сумму ряда???
Ряд сходиться или расходится??
Необходимый признак сходимости ряда и его следствие.
Ниже приведены несколько утверждений, позволяющих делать (в некоторых случаях) заключение о сходимости или расходимости рядов.
|
(необходимый признак сходимости). (1) сходится, то общий член этого ряда к нулю: lim an = 0. n→∞ |
||
|
Если ряд стремится |
n→∞
Д-во: an = Sn − Sn−1 ⎯⎯⎯→0
Внимание! Данный признак не является достаточным!
Пример: Гармонический ряд![]()
2 n n=1 n
1
расходится, но an = → 0 n
 Следствие (достаточный признак расходимости
ряда). Если lim an ≠
0, то ряд (1) расходится. n→∞
Следствие (достаточный признак расходимости
ряда). Если lim an ≠
0, то ряд (1) расходится. n→∞
Пример. Исследовать на сходимость ряд .
2n −1 ⎡∞⎤ 2−1 n 2
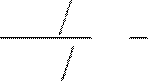 n→∞ n→∞ 3n + 2 ⎢⎣∞⎥⎦ = nlim→∞3+ 2 n = 3 ≠ 0. lim an = lim
n→∞ n→∞ 3n + 2 ⎢⎣∞⎥⎦ = nlim→∞3+ 2 n = 3 ≠ 0. lim an = lim ![]() =
= ![]()
Значит, ряд расходится.
Достаточные признаки сходимости рядов с неотрицательными членами
Теорема 4 (первый признак сравнения).
Пусть даны два ряда с неотрицательными членами:
(А)
n=1
и (В)
n=1
 Если для всех n, или начиная
с некоторого номера n=
N , выполняется неравенство an ≤ bn, то из сходимости ряда
(В) следует сходимость ряда (А), а из расходимости ряда (А) следует расходимость
ряда (В). Иначе говоря, если «больший» ряд сходится, то и «меньший» ряд
сходится; если «меньший» ряд расходится, то и «больший» ряд расходится.
Если для всех n, или начиная
с некоторого номера n=
N , выполняется неравенство an ≤ bn, то из сходимости ряда
(В) следует сходимость ряда (А), а из расходимости ряда (А) следует расходимость
ряда (В). Иначе говоря, если «больший» ряд сходится, то и «меньший» ряд
сходится; если «меньший» ряд расходится, то и «больший» ряд расходится.
∞ 2n
Пример. Исследовать ряд
∑ ![]() на
сходимость.
на
сходимость.
2n
n=1 1+ 2 Сравним данный ряд с геометрическим рядом
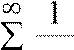 ,
,
n
n=12
который сходится как геометрический ряд со
1 2n 2n 1
![]() знаменателем q =
знаменателем q = ![]() <1. Имеем < = для
<1. Имеем < = для
2 1+ 22n 22n 2n
всех n, значит, на основании теоремы ряд сходится.
|
Пример |
![]() Решение. Сравним данный
n=1 ln(n+1)
Решение. Сравним данный
n=1 ln(n+1)
ряд с расходящимся гармоническим
рядом  .
.
1 1
![]() Поскольку > и гармонический
ряд ln(n +1) n
+1
Поскольку > и гармонический
ряд ln(n +1) n
+1
расходится, то на основании теоремы
заключаем, что ряд 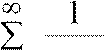 расходится.
расходится.
n=1 n+1
Теорема 5. (второй признак сравнения).
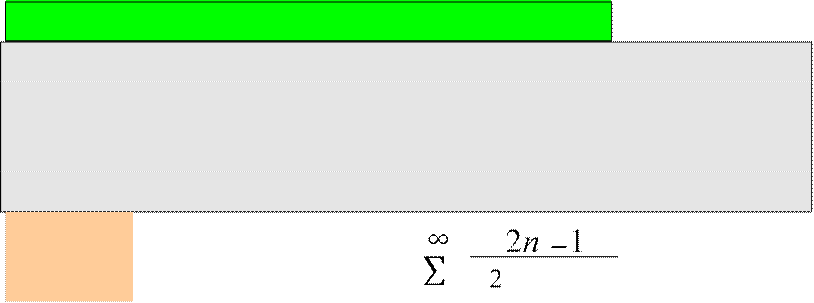 Если существует конечный, отличный
от нуля, предел an =
L, L ≠
0, L ≠ ∞,
то ряды (А) и (В) сходятся lim
Если существует конечный, отличный
от нуля, предел an =
L, L ≠
0, L ≠ ∞,
то ряды (А) и (В) сходятся lim
n→∞ bn или расходятся одновременно.
Пример. Исследовать ряд .
n=1 n − 3n + 5
Сравним данный ряд с гармоническим рядом 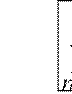 , который расходится.
Имеем
, который расходится.
Имеем
lim an = lim ![]() (2n
−1)n = lim
(2n
−1)n = lim ![]() 2n2
− n =
2n2
− n =
n→∞ bn n→∞ (n2 − 3n + 5) n→∞ n2 −3n + 5
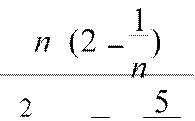
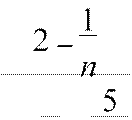 2
2
lim= lim= 2 ≠ 0. n→∞ 3 n→∞ 3
n (1− + ) 1− +
n n2 n n2
Поскольку 2 ≠ 0, то на основании теоремы заключаем, что исследуемый ряд расходится.
|
. Если для ряда a lim n+1 = l, то n→∞ an 1 ряд расходится, ― нужно |
||
|
∞ ∑ an, an > 0, существует предел n=1 при l <1 ряд сходится, при l > при l =1 вопрос остается открытым применять другие признаки. |
Признак Даламбера удобно применять в тех случаях, когда в записи общего члена ряда участвуют факториалы (!) и степени.
|
Пример. |
∞ n!
Исследовать ряд ∑ ![]() .
n
.
n
n! 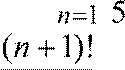
Решение. Так как an
= ![]() n
, an+1 = n+1 , то
n
, an+1 = n+1 , то
5 5
(n +1)!5n n!(n +1) 5n n+1
l = lim ![]() = lim
= lim ![]() = lim
= lim ![]() = ∞. n→∞ 5n+1 n! n→∞ 5n ⋅5⋅n! n→∞ 5
= ∞. n→∞ 5n+1 n! n→∞ 5n ⋅5⋅n! n→∞ 5
Так как ∞>1, то исследуемый ряд расходится.
Теорема 7 (признак Коши). Если для ряда ∞
∑an, an > 0, существует предел l = lim n an , n=1 n→∞
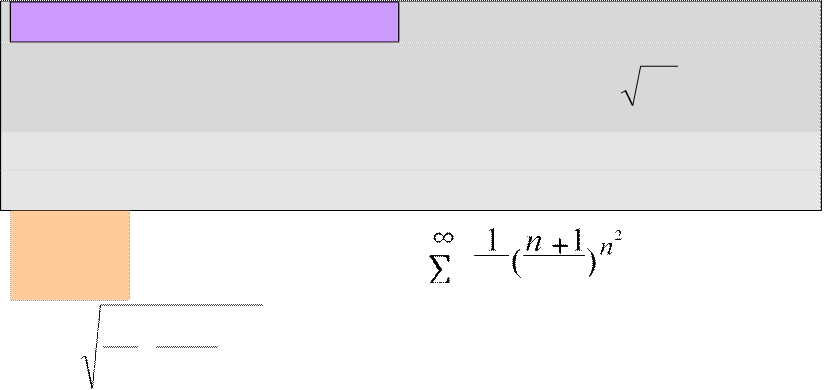 то при l
<1 ряд сходится,
при l >1
ряд расходится, а при l =1
вопрос
то при l
<1 ряд сходится,
при l >1
ряд расходится, а при l =1
вопрос
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.