Следовательно, мы будем использовать центральные моментыμk
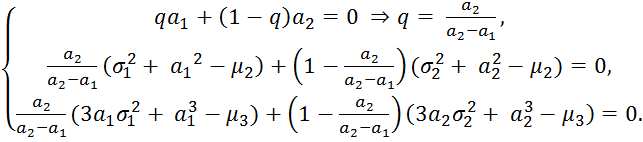 ;
;
Рассмотрим второе уравнение:
![]() ;
;
![]() ;
;
Раскрыв
скобки и приведя подобные слагаемые, получим квадратное уравнение относительно ![]() :
:
![]() ;
;
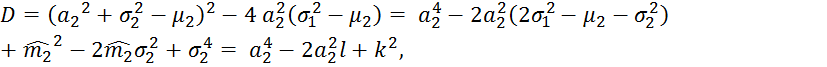
![]() ;
;
Отсюда
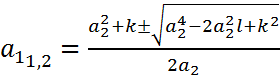 ;
;
Подставляя данное решение в третье уравнение системы получим:
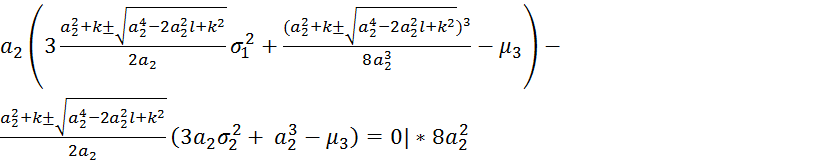 ;
;
 ;
;
Раскрыв скобки и поделив на 2:
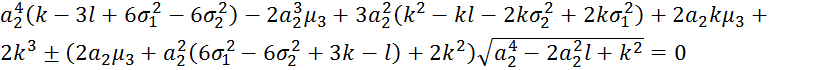 ;
;
Подставляя значения kи l:
![]() ;
;
Поделим опять на 2:
![]() ;
;
Перенесем слагаемое с корнем в правую часть и возведем в квадратуравнение:
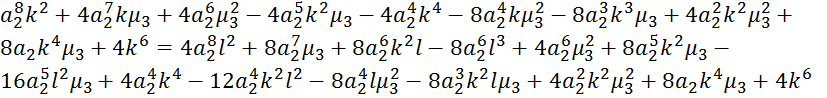 ;
;
Или
![]()
![]() ;
;
Получим уравнение пятого порядка:
![]()
![]() ;
;
Подставив значение известных параметров получим:
-4.5539203786799675047e9*a2+4.0985217266487130656e7*a22-180534.256093048632*a23+104885.95176*a24+39075.98356*a25-4.0990814284920310681e9=0
Графикфункции:
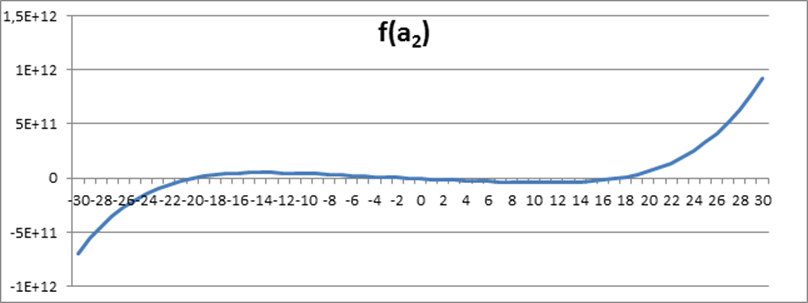
Подставляя выборочные моменты решим данное уравнение методом деления отрезка пополамс помощью математического пакета Mathcad 15. Используем этот метод, благодаря его безусловной сходимости. Он сходится, если на интервале [a, b] имеется хотя бы один корень. Кроме того, метод не использует производных.
Принцип метода деления отрезка пополам:
Пусть дано уравнение f(x)=0, функция f(x) непрерывна на интервале [a,b]. Условие f(a)* f(b)<0 указывает тогда на наличие хотя бы одного корня на этом отрезке.
1)Поделим отрезок [a,b] пополам точкой c, координата которой c=(a+b)/2 и вычислим значение функции f(c).
Возможны два случая:
а) f(a)* f(c)>0, т.е. значения функции на концах отрезка [a, c] одинаковы по знаку; тогда корень уравнения находится на отрезке [c, b] и отрезок [a, c] можно исключить из дальнейшего рассмотрения, перенеся точку a в точку c: a=c; f(a)=f(c);
б) f(a)* f(c)<0, т.е. значение функции на концах отрезка [a, c] противоположны по знаку; тогда корень находится на отрезке [a, c] и отрезок [c,b] можно исключить из дальнейшего рассмотрения, перенеся точку b в точку c: b=c.
2) После исключения правой или левой половины отрезка продолжают деление пополам до тех пор, пока длина оставшегося интервала [a, b] не станет меньше некоторой заданной малой величины ε, т.е. |b-a| <ε , и тогда любое значение аргумента из отрезка [a, b] можно считать корнем с погрешностью ε. Обычно принимают в качестве корня середину отрезка.
Корни нашего уравнения будем искатьна отрезке [0;50] с точностью ε=10-5
В процессе вычислений, был получен следующий корень уравнения
![]() ;
;
Подставляя данное решение в уравнение для ![]() ,
получим:
,
получим:
![]() ;
;
Соответственно для ![]() ,
p
= 4,29 что очевидно не является правильной оценкой, а для
,
p
= 4,29 что очевидно не является правильной оценкой, а для ![]() ,
p
= 0,704
,
p
= 0,704
Теперь вернем систему координат в исходное состояние, т.е.прибавим первый выборочный момент:
![]() ;
;
![]() ;
;
Функция правдоподобия имеет вид:
![]() ;
;
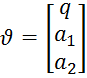 ;
;
Согласно алгоритму Ньютона искомая оценка имеет вид:
![]() ;
;
Для нахождения оценок, нам потребуется градиент и матрица вторых производных:
![]() ;
;
![]() ;
;
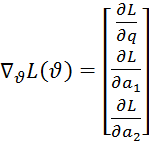 ;
;
Логарифмическая функция правдоподобия:
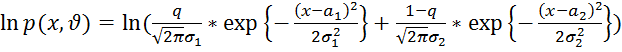 ;
;
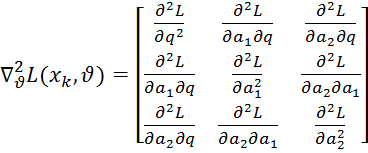 ;
;
Очевидно, что
![]() ;
;
Вычислим производные для градиента и матрицы Гессе:
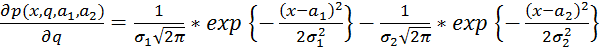 ;
;
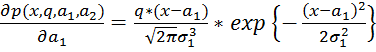 ;
;
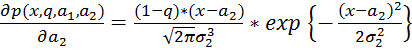 ;
;
Теперь выведем формулы производных для функции максимального правдоподобия:
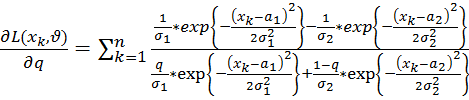 ;
;
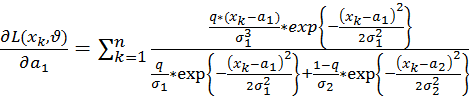 ;
;
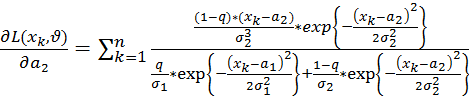 ;
;
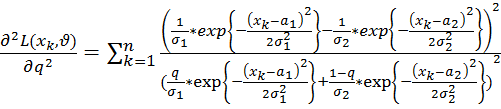 ;
;
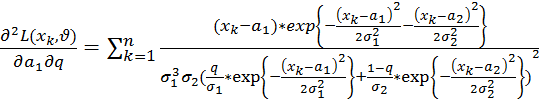 ;
;
Обозначим
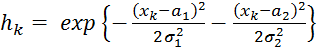 ;
;
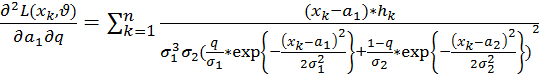 ;
;
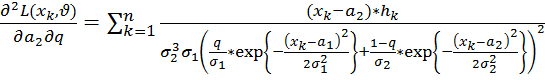 ;
;
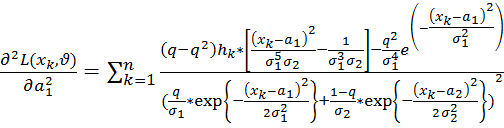 ;
;
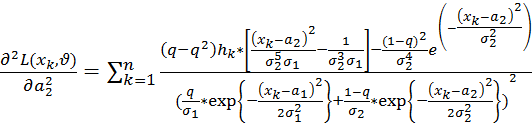 ;
;
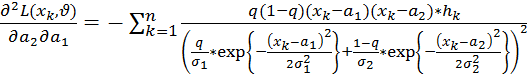 ;
;
Определитель
матрицы ![]() равен:
равен:
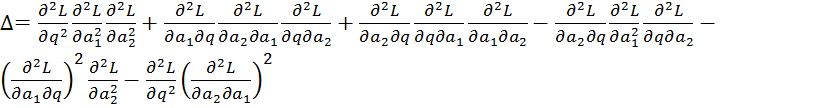 ;
;
Предполагая, что определитель матрицы не равен нулю. Найдем обратную матрицу:
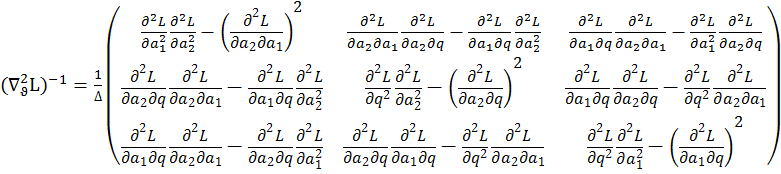 ;
;
Мы нашли все необходимые выражения для оценивания параметров с помощью метода Ньютона. Теперь можем вывести формулы оценок параметров q, a1 и a2:
 ;
;
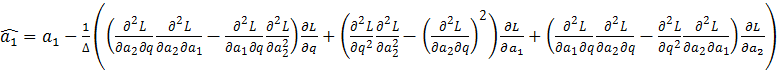 ;
;
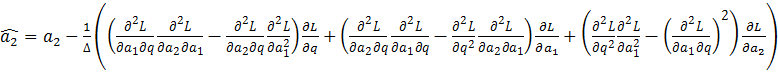 ;
;
В результате выполнения
работы методом моментов получены оценки трех параметров разделения смеси двух
нормальных распределений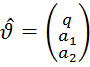 .
Полная задача о разделении смеси двух нормальных
распределений, требующая оценку пяти параметров более сложная и в данной работе
не рассматривалась. Также численно была рассчитана оценка параметров
.
Полная задача о разделении смеси двух нормальных
распределений, требующая оценку пяти параметров более сложная и в данной работе
не рассматривалась. Также численно была рассчитана оценка параметров 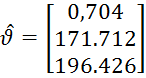 для
построенной выборки. Использовался метод деления отрезка пополам, т.к. он
хорошо сходится и не требует вычисления производных. Также получен численный алгоритм
разделения
смеси нормальных распределений метода максимального правдоподобия.
для
построенной выборки. Использовался метод деления отрезка пополам, т.к. он
хорошо сходится и не требует вычисления производных. Также получен численный алгоритм
разделения
смеси нормальных распределений метода максимального правдоподобия.
1. Севастьянов Б.А.: Курс теории вероятностей и математической статистики – М.: «Наука» 1982 г.
2. Кремер Н. Ш.: Теория вероятности и математическая статистика: Учебник 2-е издание переработанное и дополненное – М.: «Юнити» 2004 г.
3. Чистяков В.П.: Курс теории вероятностей: учебное пособие для студентов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.