Численное решение уравнения f(x)=0 методом хорд и касательных. Метод монотонной прогонки

Учебное издание

Татьяна Владимировна

ЛАБОРАТОРНЫЕ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ

Методические указания и задания для cтудентов математических cпециальноcтей

В авторской редакции

Технический редактор

Компьютерный набор и верстка Л. А. Молчановой

Подписано в печать 28.11.2007

Формат 60×84 1/16. Усл. печ. л. 1,3. Уч.-изд. л. 1,5 Тираж 50 экз.

Издательство Дальневосточного университета 690950, Владивосток, ул. Октябрьская, 27.

Отпечатано в лаборатории кафедры компьютерных наук ИМКН ДВГУ

690950, Владивосток, ул. Октябрьская, 27, к. 132.

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Дальневосточный государственный университет

ЛАБОРАТОРНЫЕ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ

Методические указания и задания для cтудентов математических cпециальноcтей

Владивосток

Издательство Дальневосточного университета 2007

.

Варианты заданий

Таблица 3. Построение сплайна через наклоны

I тип кр. усл.	II          тип усл.	кр.	IV тип кр. усл.
1	9		17	Задача интерполирования, данные из лаб. раб. 1
2	10		18	Задача интегрирования, данные из лаб. раб. 4
3	11		19	Задача дифференцирования (первая производная), данные из лаб. раб. 1
4	12		20	Задача дифференцирования (вторая производная), данные из лаб. раб. 1

Таблица 4. Построение сплайна через моменты

1 тип кр. усл.	2 тип кр. усл.	4          тип усл.	кр.
5	13	21		Задача интерполирования, данные из лаб. раб. 1
6	14	22		Задача интегрирования, данные из лаб. раб. 4
7	15	23		Задача дифференцирования (первая производная), данные из лаб. раб. 1
8	16	24		Задача дифференцирования (вторая производная), данные из лаб. раб. 1

В полях таблиц указан номер варианта.

Тема 7. Численное решение уравнения f(x)=0 методом хорд и касательных

Найти действительные корни уравнения

                                                                 f(x) = 0                                                            (1)

20

R₂(x) = f^′′′(ξ)ω₃(x)/6, ξ ∈ [x_i−₁,x_i+1], ω₃(x) = (x−x_i−₁)(x−x_i)(x−x_i+1), на [x_i−₁,x_i+1] оценить минимальное и максимальное значения f^′′′(x), а затем минимальное и максимальное значения остаточного члена R₂(x).

•  Проверить, выполняется ли неравенство minR₂ < R₂(x^∗) < maxR₂, R₂(x^∗) = L₂(x^∗) − f(x^∗). Ответить на вопрос п.3.

•  Построить таблицу разделенных разностей по узлам x_i−₁, x_i,x_i+1. Вычислить интерполяционные многочлены Ньютона:

L₁(x^∗) = f(x_i) + f(x_i,x_i+1)(x^∗ − x_i) и

L₂(x^∗) = f(x_i−1)+f(x_i−1,x_i)(x^∗−x_i−1)+f(x_i−1,x_i,x_i+1)(x^∗−x_i−1)·(x^∗−x_i). Сравнить с соответствующими результатами, полученными по формулам Лагранжа.

Таблица 1.

№	y=f(x)	[a,b]	x∗	x∗∗	x∗∗∗	x∗∗∗∗
1	y=x2+ln(x)	[0.4,0.9]	0.52	0.42	0.87	0.67
2	y=x2−lg(x + 2)	[0.5,1.0]	0.53	0.52	0.97	0.73
3	y=x2+ln(x) − 4	[1.5,2.0]	1.52	1.52	1.97	1.77
4	y=(x-1)2 -0.5ex	[0.1,0.6]	0.13	0.12	0.57	0.33
5	y=(x-1)2 -e−x	[1.0,1.5]	1.07	1.02	1.47	1.27
6	y=x3−sin(x)	[0.6,1.1]	0.92	0.62	1.07	0.83
7	y=4x−cos(x)	[0.1,0.6]	0.37	0.12	0.57	0.37
8	y=x2−sin(x)	[0.5,1.0]	0.77	0.52	0.97	0.73
9	y=x−cos(x)	[0.5,1.0]	0.92	0.53	0.98	0.77
10	y=x2−cos(πx)	[0.1,0.6]	0.37	0.12	0.58	0.33
11	y=x2−sin(πx)	[0.4,0.9]	0.53	0.43	0.86	0.67
12	y=x2−cos(0.5πx)	[0.4,0.9]	0.64	0.42	0.87	0.63
13	y = x − 2cos(0.5πx)	[0.4,0.9]	0.71	0.43	0.87	0.67
14	y=x−sin(πx)	[0.6,1.1]	0.88	0.63	1.08	0.83
15	y=2x−cos(x)	[0.1,0.6]	0.44	0.13	0.58	0.37
16	y=x2+ln(x + 5)	[0.5,1.0]	0.73	0.52	0.97	0.73
17	y=0.5x2+cos(2x)	[0.6,1.1]	0.84	0.62	1.07	0.83
18	y=x2 − 0.5e−x	[0.1,0.6]	0.37	0.12	0.58	0.33
19	y=x2+lg(x)	[0.4,0.9]	0.53	0.43	0.86	0.67
20	y=x−lg(x + 2)	[0.5,1.0]	0.77	0.52	0.97	0.73
21	y=x2−lg(0.5x)	[0.5,1.0]	0.92	0.53	0.98	0.77
22	y=x3−cos(2x)	[0.1,0.6]	0.37	0.12	0.58	0.33
23	y=x2+cos(πx/2)	[0.1,0.6]	0.13	0.12	0.57	0.33
24	y=x/2−cos(x/2)	[0.4,0.9]	0.64	0.42	0.87	0.63

5

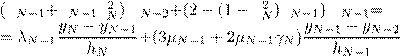Умножая первое уравнение на λ_N−₁ и складывая со вторым, получают: µ       λ             γ             m              γ             λ             m

.

С учетом того, что

                          h2N                      hN                                   h2N

µN−1+λN−1h2_N−1 = h_N + h_N−₁ + (h_N + h_N−₁)h_N−₁ = µN−1(1+γN) = γN,

2 − λ_N−1 + λ_N−1γ_N² = 1 + µ_N−1 + µ_N−1γ_N = 1 + µ_N−1(1 + γ_N) = 1 + γ_N,

имеют

.

Итак, в случае краевых условий 4-ого типа имеют:

;

2;

.

4. Построение кубического сплайна через моменты

Моментами называются;

 на [x_i, x_i+1],

               ′                                                                (x − x_i)²

S (x) = c_i + a_i(x − x_i) + b_i,

2 S^′′(x) = a_i + b_i(x − x_i),

S′′′(x) = bi, S′′(xi) = ai = Mi; S′′(xi+1) = ai + bihi+1 ⇒ bi = Mi+1 − Mi. hi+1

Отсюда:, тогда

.

Из условия непрерывности первой производной для S(x) в узлах x_i, имеют:

,

16

16. n = 4,      t_1,4 = ±0,861136,           c₁ = c₄ = 0,347855, t_2,3 = ±0,339981