























Страницы 513-523
Лекция 13
Многомерные процессы
До сих пор мы рассматривали модели, которые состоят только из одного соотношения, связывающего временные ряды. При этом мы выбирали одну из переменных в качестве эндогенной, а остальные переменные являлись экзогенными. Такое разделение не всегда является естественным, часто приходится рассматривать одновременно несколько соотношений, в которые одни и те же переменные входят и как эндогенные, и как экзогенные. Как видно из прошлой лекции, переменная не всегда может рассматриваться как экзогенная, и мы фактически должны рассматривать модель DGP, состоящую из нескольких уравнений. Это означает моделирование нескольких временных рядов одновременно, другими словами - моделирование многомерного случайного процесса.
Начнем с определении. Рассмотрим вектор ![]() =(хt1,хt2,...,хtk)T , каждая компонента которого
является временным рядом. верхним индексом будем обозначать номер компоненты, а
нижним по-прежнему - момент времени. распределение компонент характеризуется
семейством совместных плотностей распределения вида: fn(хt1i1,хt2i2,..., хtnin)‚ n=1‚2,.... Условием стационарности в узком
смысле по-прежнему является независимость от сдвига во времени всего семейства
совместных плотностей распределения. Только теперь кроме всевозможных
комбинаций значений случайного процесса в различные моменты времени аргументами
плотностей вероятности также являются всевозможные комбинации различных
компонент в различные моменты времени. Например, для двухмерной плотности получаем из условия стационарности: f2(хt1,хt2) = f2(х1t+r, х2t+r) для любого τ. Совместное распределение компонент для одного и
того же момента времени не зависит от времени. Рассмотрим другую функцию
распределения, например трехмерную, в которую входят значения первой компоненты
в два разных момента времени и второй компоненты в некоторый третий момент
времени. Стационарность означает, чтоf3(хt1 ,хt+h1,хt+s2) = f3(х1t+τ , х2t+s+τ) .
Можно сказать, что это свойство инвариантности к сдвигу во времени. То есть,
если к каждому моменту времени прибавить величину τ, то функция плотности не изменится. Понятно, что стационарность
многомерного процесса влечет за собой стационарность каждой из его компонент.
=(хt1,хt2,...,хtk)T , каждая компонента которого
является временным рядом. верхним индексом будем обозначать номер компоненты, а
нижним по-прежнему - момент времени. распределение компонент характеризуется
семейством совместных плотностей распределения вида: fn(хt1i1,хt2i2,..., хtnin)‚ n=1‚2,.... Условием стационарности в узком
смысле по-прежнему является независимость от сдвига во времени всего семейства
совместных плотностей распределения. Только теперь кроме всевозможных
комбинаций значений случайного процесса в различные моменты времени аргументами
плотностей вероятности также являются всевозможные комбинации различных
компонент в различные моменты времени. Например, для двухмерной плотности получаем из условия стационарности: f2(хt1,хt2) = f2(х1t+r, х2t+r) для любого τ. Совместное распределение компонент для одного и
того же момента времени не зависит от времени. Рассмотрим другую функцию
распределения, например трехмерную, в которую входят значения первой компоненты
в два разных момента времени и второй компоненты в некоторый третий момент
времени. Стационарность означает, чтоf3(хt1 ,хt+h1,хt+s2) = f3(х1t+τ , х2t+s+τ) .
Можно сказать, что это свойство инвариантности к сдвигу во времени. То есть,
если к каждому моменту времени прибавить величину τ, то функция плотности не изменится. Понятно, что стационарность
многомерного процесса влечет за собой стационарность каждой из его компонент.
Как и в одномерном случае, стационарность в узком
смысле влечет за собой ряд свойств характеристик случайных процессов. Прежде
всего, начнем с математического ожидания. Математическое ожидание для каждой
компоненты не зависит от других компонент. Поэтому если многомерный процесс
стационарен, математическое ожидание каждой компоненты не зависит от времени.
Вектор математических ожиданий E(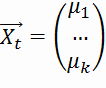 не зависит от
времени.
не зависит от
времени.
Теперь рассмотрим моменты второго порядка. Каждая компонента характеризуется дисперсией и автокорреляционной функцией. Если одномерный ряд стационарен, его автокорреляционная и автоковариационная функции зависят только от сдвига τ: Corr(τ) = Corr(хti,хjt+r) = рi(τ), однако теперь можно рассмотреть второй смешанный момент для различных компонент, а также Corr(хti,хjt+r). Такую величину естественно назвать кросс-корреляционной функцией. Если компоненты образуют многомерный стационарный процесс, то кросс-корреляция будет функцией сдвига во времени τ. Обозначим эту функцию Rij(τ). Довольно очевидно, что Rij(τ) = Rji(-τ). При фиксированном значении τ элементы Rij(τ) образуют матрицу R, зависящую от τ. Значению τ, равному нулю, соответствует корреляционная матрица вектора
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.